25.2: Phase Diagrams for Binary Mixtures
- Page ID
- 238276
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As suggested by the Gibbs Phase Rule, the most important variables describing a mixture are pressure, temperature and composition. In the case of single component systems, composition is not important so only pressure and temperature are typically depicted on a phase diagram. However, for mixtures with two components, the composition is of vital important, so there is generally a choice that must be made as to whether the other variable to be depicted is temperature or pressure.
Temperature-composition diagrams are very useful in the description of binary systems, many of which will for two-phase compositions at a variety of temperatures and compositions. In this section, we will consider several types of cases where the composition of binary mixtures are conveniently depicted using these kind of phase diagrams.
Partially Miscible Liquids
A pair of liquids is considered partially miscible if there is a set of compositions over which the liquids will form a two-phase liquid system. This is a common situation and is the general case for a pair of liquids where one is polar and the other non-polar (such as water and vegetable oil.) Another case that is commonly used in the organic chemistry laboratory is the combination of diethyl ether and water. In this case, the differential solubility in the immiscible solvents allows the two-phase liquid system to be used to separate solutes using a separatory funnel method.
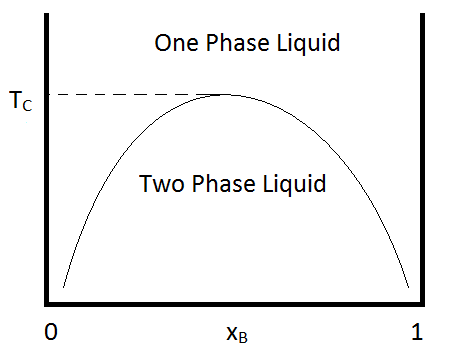
As is the case for most solutes, their solubility is dependent on temperature. For many binary mixtures of immiscible liquids, miscibility increases with increasing temperature. And then at some temperature (known as the upper critical temperature), the liquids become miscible in all compositions. An example of a phase diagram that demonstrates this behavior is shown in Figure \(\PageIndex{1}\). An example of a binary combination that shows this kind of behavior is that of methyl acetate and carbon disufide, for which the critical temperature is approximately 230 K at one atmosphere (Ferloni & Spinolo, 1974). Similar behavior is seen for hexane/nitrobenzene mixtures, for which the critical temperature is 293 K.
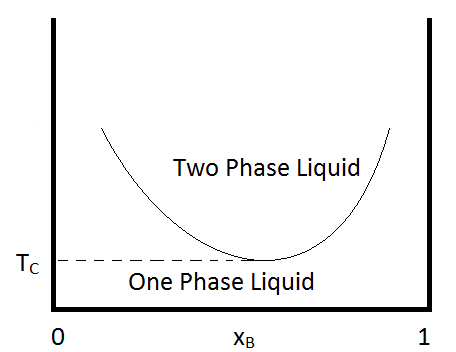
Another condition that can occur is for the two immiscible liquids to become completely miscible below a certain temperature, or to have a lower critical temperature. An example of a pair of compounds that show this behavior is water and trimethylamine. A typical phase diagram for such a mixture is shown in Figure \(\PageIndex{2}\). Some combinations of substances show both an upper and lower critical temperature, forming two-phase liquid systems at temperatures between these two temperatures. An example of a combination of substances that demonstrate the behavior is nicotine and water.
The Lever Rule
The composition and amount of material in each phase of a two phase liquid can be determined using the lever rule. This rule can be explained using the following diagram.
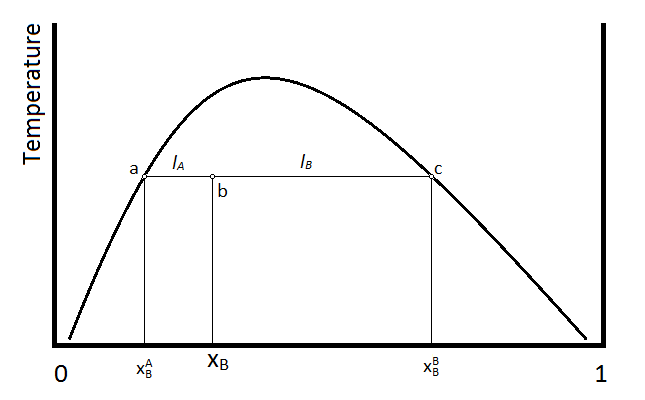
Suppose that the temperature and composition of the mixture is given by point b in the above diagram. The horizontal line segment that passes through point b, is terminated at points a and c, which indicate the compositions of the two liquid phases. Point a indicates the mole faction of compound B (\(X_B^A\)) in the layer that is predominantly A, whereas the point c indicates the composition (\(X_B^B\) )of the layer that is predominantly compound B. The relative amounts of material in the two layers is then inversely proportional to the length of the tie-lines a-b and b-c, which are given by \(l_A\) and \(l_B\) respectively. In terms of mole fractions,
\[ l_A = X_B - X_B^A\]
and
\[ l_B = X_B^B - X_B \]
The number of moles of material in the A layer (\(n_A\)) and the number of moles in the B layer (\(n_B\)) are inversely proportional to the lengths of the two lines \(l_A\) and \(l_B\).
\[ n_A l_A = n_B l_B\]
Or, substituting the above definitions of the lengths \(l_A\) and \(l_B\), the ratio of these two lengths gives the ratio of moles in the two phases.
\[ \dfrac{n_A}{n_B} = \dfrac{l_B}{l_A} = \dfrac{ X_B^B - X_B}{X_B - X_B^A}\]
Contributors
Patrick E. Fleming (Department of Chemistry and Biochemistry; California State University, East Bay)


