4.2: Cyanine Dyes
- Page ID
- 4489
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
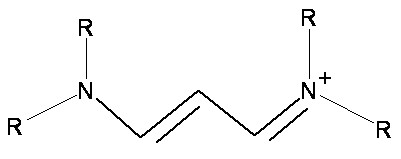
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cyanine dye molecules, which have the general structure shown in Figure \(\PageIndex{1}\), are planar cations. The number of carbon atoms in the chain can vary, as can the nature of the end groups containing the nitrogen atoms. The R groups in the diagram represent \(H\), \(CH_3\), \(CH_3CH_2\), or many other moieties including ring structures. Since these dyes are cations, they can be paired with many anions, e.g. \(I^-\), iodide. The position (wavelength) and strength (absorption coefficient) of the absorption band depends upon the length of the carbon chain between the nitrogen atoms but is not affected very much by the nature of the end groups beyond the nitrogen atoms.
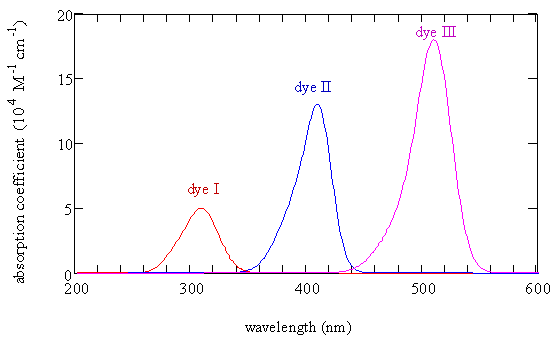
These molecules are called dye molecules because they have very intense absorption bands in the visible region of the spectrum as shown in Figure \(\PageIndex{2}\). This strong absorption of light at particular wavelengths makes solutions of these molecules brightly colored. A solution of a dye shows the color of the light that is not absorbed. The strong absorption leads to many applications in technology. For example, dyes are used to color plastics, fabrics, and hair. They also can be used as filters to produce colored light and as a laser medium in medical applications.
Example \(\PageIndex{1}\)
Draw the Lewis electron dot structure of dye I that produced the spectrum shown in Figure \(\PageIndex{2}\) with the maximum absorption at 309 nm. Examine the resonance structures and determine whether all the carbon-carbon bonds are identical or whether some are single bonds and some are double bonds.
Example \(\PageIndex{2}\)
Use Figure \(\PageIndex{2}\) to describe what happens to the maximum absorption coefficient and the wavelength of the peak absorption as the length of a cyanine dye molecule increases.
Example \(\PageIndex{3}\)
The decadic molar absorption coefficient for dye III at λ = 512 nm is almost 200,000 in units of \(1000 cm^2/mol\). If 0.1 gram of dye III (very small) were dissolved in 10 liters of water (very large), what fraction of light at 512 nm would be absorbed in a path length of 1 mm (very small)? What is the concentration of this solution? What insight do you gain from your results? (Note: the molar mass is 179 g/mol.)
The electrons and bonds in the cyanine dyes can be classified as sigma or pi. The probability densities for the sigma electrons are large along the lines connecting the nuclei, while the probability densities for the pi electrons are large above and below the plane containing the nuclei. In molecular orbital theory, the \(\pi\) electrons can be described by wavefunctions composed from \(p_z\) atomic orbitals, shown in Figure \(\PageIndex{3}\).
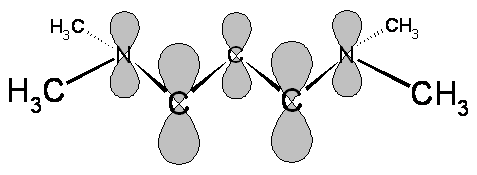
Example \(\PageIndex{4}\)
Determine the number of pi electrons in each of the three molecules described in Figure \(\PageIndex{2}\).
The pi electrons in these molecules, one from each carbon atom and three from the two nitrogen atoms, are delocalized over the length of the molecule between the nitrogen atoms. When ultraviolet and visible light is absorbed by the cyanine dyes, the energy is used to cause transitions of the pi electrons from one energy level to another, as sketched in Figure \(\PageIndex{4}\). The longest wavelength transition occurs from the highest-energy occupied level to the lowest-energy unoccupied level. We will use Quantum Mechanics and a simple model, called the particle-in-a-box model, to explain why the longer molecules absorb at longer wavelengths and have larger absorption coefficients. This analysis will demonstrate that Quantum Mechanics is a quantitative theory. It provides both a qualitative understanding of chemical systems and numerical values for the properties of interest. Both are important for understanding molecules and their chemistry.
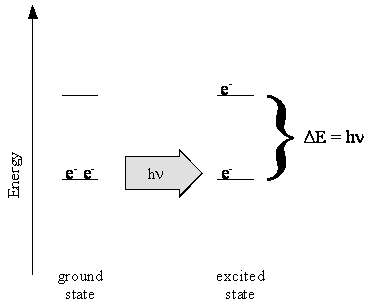
You can visualize the absorption of energy and the promotion of an electron from a lower energy level to a higher one like throwing a shirt from your closet floor to a shelf. There is an important difference however. You can see the shirt on the way from the floor to the shelf. You can tell when it left the floor, and when it arrived on the shelf. Such precise information cannot be obtained for the electron. We only know the probability that the electron is in the lower level and the probability that it is in the higher level as a function of time. We do not know exactly when during this period that the electron makes the transition from one energy level to the other.
We can imagine that the potential energy experienced by the pi electron varies along the chain as shown in Figure \(\PageIndex{5}\) effectively trapping the electron in the pi region of the molecule, i.e. in a one-dimensional box. At the end of the chain the potential energy rises to a large value. The particle-in-a-box model essentially consists of three approximations to the actual potential energy.
- The chain of carbon atoms forms a one-dimensional space of some length L for the pi electrons.
- The potential energy is constant along the chain; i.e. the oscillations are ignored.
- The potential energy becomes infinite at some point slightly past the nitrogen atoms.
Since only changes in energy are meaningful, and an absolute zero of energy does not exist, the constant potential energy of the electron along the chain between the nitrogen atoms can be defined as zero. The particle-in-a-box potential energy also is shown in Figure \(\PageIndex{5}\).
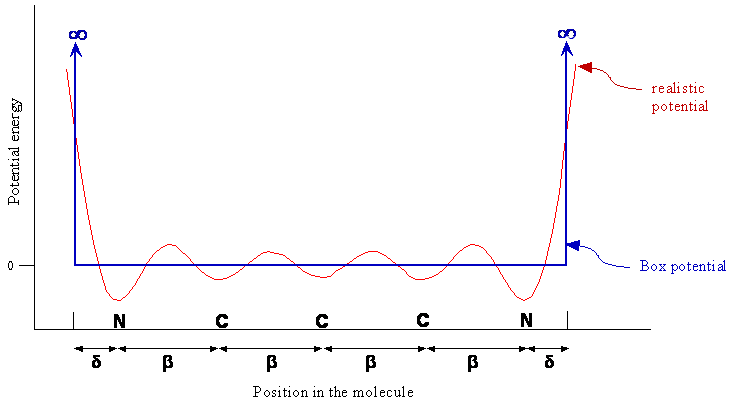
The particle-in-a-box model allows us to relate the transition energy obtained from the position of the absorption maximum to the length of the conjugated part of the molecule, i.e. distance L between the infinite potential barriers at the ends of the molecule. From this distance for different series of dyes, we can obtain the average bond length β and the distance δ the box extends beyond a nitrogen atom for each series. If this model is reasonable, we expect the average bond lengths to be similar for each series and δ to vary from one series to another due to differences in the end groups attached to the nitrogen atoms. Some end groups might, due to their polarizability or electronegativity, allow the electrons to penetrate further past the nitrogen atoms than others. Analyzing the data in this way rather than using estimated bond lengths to predict transition energies was suggested by R.S. Moog. (J. Chem Educ. 1991, 68, 506-508.)
Example \(\PageIndex{5}\)
In Figure \(\PageIndex{5}\), why does a realistic potential energy dip at each atom? Why is the dip larger for nitrogen than for carbon? Why does the potential energy increase sharply at the ends of the molecule?


