6.2: Orbitals
- Page ID
- 162846
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Hartree Description
The energies and wave functions within the most commonly used theories of atomic structure are assumed to arise as solutions of a Schrödinger equation whose Hamiltonian \(h_e(r)\) possess three kinds of energies:
- Kinetic energy, whose average value is computed by taking the expectation value of the kinetic energy operator \(-\dfrac{\hbar^2}{2m} \nabla^2\) with respect to any particular solution \(\phi_j(r)\) to the Schrödinger equation: \[KE = \langle\phi_j| -\dfrac{\hbar^2}{2m} \nabla^2 |\phi_j\rangle \]
- Coulombic attraction energy with the nucleus of charge \(Z\): \[\langle\phi_j| -\dfrac{Z_e^2}{r} |\phi_j\rangle\]
- Coulomb repulsion energies with all of the \(N-1\) other electrons, which are assumed to occupy other atomic orbitals (AOs) denoted \(\phi_K\), with this energy computed as
\[\sum_K \langle\phi_j(r) \phi_K(r’) |\frac{e^2}{|r-r’|} | \phi_j(r) \phi_K(r’)\rangle.\label{6.1.2}\]
The Dirac notation \(\langle\phi_j(r) \phi_K(r’) |\dfrac{e^2}{|r-r’|} | \phi_j(r) \phi_K(r’)\rangle\) is used to represent the six-dimensional Coulomb integral
\[J_{J,K} = \int |\phi_j(r)|^2 |\phi_K(r’)|^2 \dfrac{e^2}{r-r'} dr dr’ \label{6.1.3}\]
that describes the Coulomb repulsion between the charge density \(|\phi_j(r)|^2\) for the electron in \(\phi_j\) and the charge density \(|\phi_K(r’)|^2\) for the electron in \(\phi_K\). Of course, the sum over \(K\) must be limited to exclude \(K=J\) to avoid counting a “self-interaction” of the electron in orbital \(\phi_j\) with itself.
The total energy \(\epsilon_J\) of the orbital \(\phi_j\), is the sum of the above three contributions:
\[\epsilon_J = \langle\phi_j| - \frac{\hbar^2}{2m} \nabla^2 |\phi_j\rangle + \langle\phi_j| -\frac{Z_e^2}{r} |\phi_j\rangle + \sum_K \langle\phi_j(r) \phi_K(r’) |\frac{e^2}{|r-r’|} | \phi_j(r) \phi_K(r’)\rangle.\label{6.1.4}\]
This treatment of the electrons and their orbitals is referred to as the Hartree-level of theory. As stated above, when screened hydrogenic AOs are used to approximate the \(\phi_j\) and \(\phi_K\) orbitals, the resultant \(\epsilon_J\) values do not produce accurate predictions. For example, the negative of \(\epsilon_J\) should approximate the ionization energy for removal of an electron from the AO \(\phi_j\). Such ionization potentials (IP s) can be measured, and the measured values do not agree well with the theoretical values when a crude screening approximation is made for the AO s.
LCAO-Expansion
To improve upon the use of screened hydrogenic AOs, it is most common to approximate each of the Hartree AOs {\(\phi_K\)} as a linear combination of so-called basis AOs {\(\chi_\mu\)}:
\[\phi_J = \sum_\mu C_{J,\mu} \chi_\mu.\label{6.1.5}\]
using what is termed the linear-combination-of-atomic-orbitals (LCAO) expansion. In this equation, the expansion coefficients {\(C_{J,\mu}\)} are the variables that are to be determined by solving the Schrödinger equation
\[h_e \phi_J = \epsilon_J \phi_J. \label{6.1.6}\]
After substituting the LCAO expansion for \(\phi_J\) into this Schrödinger equation, multiplying on the left by one of the basis AOs \(\chi_\nu\), and then integrating over the coordinates of the electron in \(\phi_J\), one obtains
\[\sum_\mu \langle\chi_\nu| h_e| \chi_\mu\rangle C_{J,\mu} = \epsilon_J \sum_\mu \langle\chi_\nu| \chi_\mu\rangle C_{J,\mu} . \label{6.1.7}\]
This is a matrix eigenvalue equation in which the \(\epsilon_J\) and {\(C_{J,\mu}\)} appear as eigenvalues and eigenvectors. The matrices \(\langle\chi_\nu| h_e| \chi_\mu\rangle\) and \(\langle\chi_\nu| \chi_\mu\rangle\) are called the Hamiltonian and overlap matrices, respectively. An explicit expression for the former is obtained by introducing the earlier definition of he:
\[\langle\chi_\nu| h_e| \chi_\mu\rangle = \langle\chi_\nu| - \frac{\hbar^2}{2m} \nabla^2 |\chi_\mu\rangle + \langle\chi_\nu| -\frac{Ze^2}{r} |\chi_\mu\rangle \label{6.1.8}\]
\[+ \sum_{\eta,\gamma} \sum_K C_{K,\eta} C_{K,\gamma} \langle\chi_\nu(r) \chi_\eta(r’) |\frac{e^2}{|r-r’|} | \chi_\mu(r) \chi_\gamma(r’)\rangle. \label{6.1.9}\]
An important thing to notice about the form of the matrix Hartree equations is that to compute the Hamiltonian matrix, one must know the LCAO coefficients {\(C_{K,\gamma}\)} of the orbitals which the electrons occupy. On the other hand, these LCAO coefficients are supposed to be found by solving the Hartree matrix eigenvalue equations. This paradox leads to the need to solve these equations iteratively in a so-called self-consistent field (SCF) technique. In the SCF process, one inputs an initial approximation to the {\(C_{K,\gamma}\)} coefficients. This then allows one to form the Hamiltonian matrix defined above. The Hartree matrix equations
\[\sum_\mu \langle\chi_\nu| h_e| \chi_\mu\rangle C_{J,m} = \epsilon_J \sum_\mu \langle\chi_\nu| \chi_\mu\rangle C_{J,\mu} \label{6.1.10}\]
are then solved for new {\(C_{K,\gamma}\)} coefficients and for the orbital energies {\(\epsilon_K\)}. The new LCAO coefficients of those orbitals that are occupied are then used to form a new Hamiltonian matrix, after which the Hartree equations are again solved for another generation of LCAO coefficients and orbital energies. This process is continued until the orbital energies and LCAO coefficients obtained in successive iterations do not differ appreciably. Upon such convergence, one says that a self-consistent field has been realized because the {\(C_{K,\gamma}\)} coefficients are used to form a Coulomb field potential that details the electron-electron interactions.
Basis Sets
Slater-type orbitals and Gaussian-type orbitals
As noted above, it is possible to use the screened hydrogenic orbitals as the {\(\chi_\mu\)}. However, much effort has been expended at developing alternative sets of functions to use as basis orbitals. The result of this effort has been to produce two kinds of functions that currently are widely used. The basis orbitals commonly used in the LCAO process fall into two primary classes:
- Slater-type orbitals (STOs) \[c_{n,l,m} (r,\theta,\phi) = N_{n,l,m,z} Y_{l,m} (\theta,\phi) r_{n-1} e^{-zr}\] are characterized by quantum numbers \(n\), \(l\), and \(m\) and exponents (which characterize the orbital’s radial size) \(z\). The symbol \(N_{n,l,m,z}\) denotes the normalization constant.
- Cartesian Gaussian-type orbitals (GTOs) \[c_{a,b,c} (r,\theta,\phi) = N'_{a,b,c,a} x_a y_b z_c e^{-ar^2}\] are characterized by quantum numbers \(a\), \(b\), and \(c\), which detail the angular shape and direction of the orbital, and exponents \(a\) which govern the radial size.
For both types of AOs, the coordinates \(r\), \(\theta\), and \(\phi\) refer to the position of the electron relative to a set of axes attached to the nucleus on which the basis orbital is located. Note that Slater-type orbitals (STO's) are similar to hydrogenic orbitals in the region close to the nucleus. Specifically, they have a non-zero slope near the nucleus
\[\dfrac{d}{dr}(e^{-zr})_{r=0} = -z.\]
In contrast, GTOs, have zero slope near \(r=0\) because
\[\dfrac{d}{dr}(e^{-ar^2})_{r=0} = 0.\]
We say that STOs display a cusp at \(r=0\) that is characteristic of the hydrogenic solutions, whereas GTOs do not. Although STOs have the proper cusp behavior near nuclei, they are used primarily for atomic and linear-molecule calculations because the multi-center integrals
\[\langle\chi_\mu(1) \chi_\kappa(2)|\dfrac{e^2}{|r_1-r_2|}| \chi_\nu(1) \chi_\gamma(2)\rangle\label{6.1.11}\]
which arise in polyatomic-molecule calculations (we will discuss these integrals later in this Chapter) cannot efficiently be evaluated when STOs are employed. In contrast, such integrals can routinely be computed when GTOs are used. This fundamental advantage of GTOs has lead to the dominance of these functions in molecular quantum chemistry.
To overcome the primary weakness of GTO functions (i.e., their radial derivatives vanish at the nucleus), it is common to combine two, three, or more GTOs, with combination coefficients which are fixed and not treated as LCAO parameters, into new functions called contracted GTOs (CGTOs). Typically, a series of radially tight, medium, and loose GTOs are multiplied by contraction coefficients and summed to produce a CGTO that approximates the proper cusp at the nuclear center (although no such combination of GTOs can exactly produce such a cusp because each GTO has zero slope at \(r = 0\).
Although most calculations on molecules are now performed using Gaussian orbitals, it should be noted that other basis sets can be used as long as they span enough of the regions of space (radial and angular) where significant electron density resides. In fact, it is possible to use plane wave orbitals of the form
\[\chi(r,\theta,\phi) = N\exp[i(k_x r \sin{\theta} \cos{\phi} + k_y r \sin_{\theta} \sin{\phi} + k_z r \cos{\theta})],\label{6.1.12}\]
where \(N\) is a normalization constant and \(k_x\), \(k_y\), and \(k_z\) are quantum numbers detailing the momenta or wavelength of the orbital along the \(x\), \(y\), and \(z\) Cartesian directions. The advantage to using such simple orbitals is that the integrals one must perform are much easier to handle with such functions. The disadvantage is that one must use many such functions to accurately describe sharply peaked charge distributions of, for example, inner-shell core orbitals while still retaining enough flexibility to also describe the much smoother electron density in the valence regions. Much effort has been devoted to developing and tabulating in widely available locations sets of STO or GTO basis orbitals for main-group elements and transition metals. This ongoing effort is aimed at providing standard basis set libraries which:
- Yield predictable chemical accuracy in the resultant energies.
- Are cost effective to use in practical calculations.
- Are relatively transferable so that a given atom's basis is flexible enough to be used for that atom in various bonding environments (e.g., hybridization and degree of ionization).
Fundamental Core and Valence Basis
In constructing an atomic orbital basis, one can choose from among several classes of functions. First, the size and nature of the primary core and valence basis must be specified. Within this category, the following choices are common:
- A minimal basis in which the number of CGTO orbitals is equal to the number of core and valence atomic orbitals in the atom.
- A double-zeta (DZ) basis in which twice as many CGTOs are used as there are core and valence atomic orbitals. The use of more basis functions is motivated by a desire to provide additional variational flexibility so the LCAO process can generate molecular orbitals of variable diffuseness as the local electronegativity of the atom varies. A valence double-zeta (VDZ) basis has only one CGTO to represent the inner-shell orbitals, but uses two sets of CGTOs to describe the valence orbitals.
- A triple-zeta (TZ) basis in which three times as many CGTOs are used as the number of core and valence atomic orbitals (of course, there are quadruple-zeta and higher-zeta bases also). Moreover, there are VTZ bases that treat the inner-shell orbitals with one CGTO and the valence orbitals with three CGTOs.
Optimization of the orbital exponents (z’s or a's) and the GTO-to-CGTO contraction coefficients for the kind of bases described above has undergone considerable growth in recent years. The theory group at the Pacific Northwest National Labs (PNNL) offer a world wide web site from which one can find (and even download in a form prepared for input to any of several commonly used electronic structure codes) a wide variety of Gaussian atomic basis sets. This site can be accessed here. Professor Kirk Peterson at Washington State University is involved in the PNNL basis set development project, but he also hosts his own basis set site.
Polarization Functions
One usually enhances any core and valence basis set with a set of so-called polarization functions. They are functions of one higher angular momentum than appears in the atom's valence orbital space (e.g., \(d\)-functions for C, N, and O and \(p\)-functions for H), and they have exponents (\(z\) or \(a\)) which cause their radial sizes to be similar to the sizes of the valence orbitals ( i.e., the polarization \(p\) orbitals of the H atom are similar in size to the \(1s\) orbital rather than to the \(2s\) valence orbital of hydrogen). Thus, they are not orbitals which describe the atom's valence orbital with one higher l-value; such higher-l valence orbitals would be radially more diffuse.
A primary purpose of polarization functions is to give additional angular flexibility to the LCAO process in forming bonding orbitals between pairs of valence atomic orbitals. This is illustrated in Figure 6.1.2 where polarization dp orbitals on C and O are seen to contribute to formation of the bonding \(p\) orbital of a carbonyl group by allowing polarization of the carbon atom's \(p_\pi\) orbital toward the right and of the oxygen atom's \(p_\pi\) orbital toward the left.
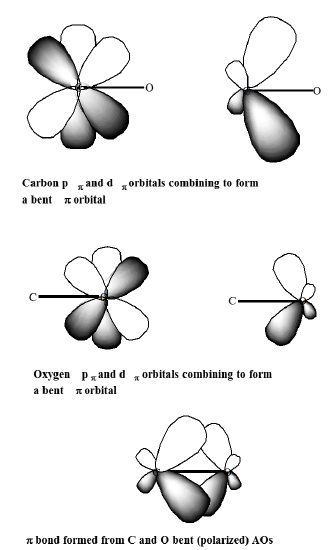
Polarization functions are essential in strained ring compounds such as cyclopropane because they provide the angular flexibility needed to direct the electron density into regions between bonded atoms, but they are also important in unstrained compounds when high accuracy is required.
Diffuse Functions
When dealing with anions or Rydberg states, one must further augment the AO basis set by adding so-called diffuse basis orbitals. The valence and polarization functions described above do not provide enough radial flexibility to adequately describe either of these cases. The PNNL web site data base cited above offers a good source for obtaining diffuse functions appropriate to a variety of atoms as does the site of Prof. Kirk Peterson.
Once one has specified an atomic orbital basis for each atom in the molecule, the LCAO-MO procedure can be used to determine the \(\chi_{\mu,i}\) coefficients that describe the occupied and virtual (i.e., unoccupied) orbitals. It is important to keep in mind that the basis orbitals are not themselves the SCF orbitals of the isolated atoms; even the proper atomic orbitals are combinations (with atomic values for the \(\chi_{\mu,i}\) coefficients) of the basis functions. The LCAO-MO-SCF process itself determines the magnitudes and signs of the \(\chi_{\nu,i}\). In particular, it is alternations in the signs of these coefficients allow radial nodes to form.


