Hofmann Elimination

Elimination reactions of 4º-ammonium salts are termed Hofmann eliminations. Since the counter anion in most 4º-ammonium salts is halide, this is often replaced by the more basic hydroxide ion through reaction with silver hydroxide (or silver oxide). The resulting hydroxide salt must then be heated (100 - 200 ºC) to effect the E2-like elimination of a 3º-amine. Example #1 below shows a typical Hofmann elimination. Obviously, for an elimination to occur one of the alkyl substituents on nitrogen must have one or more beta-hydrogens, as noted earlier in examining elimination reactions of alkyl halides.

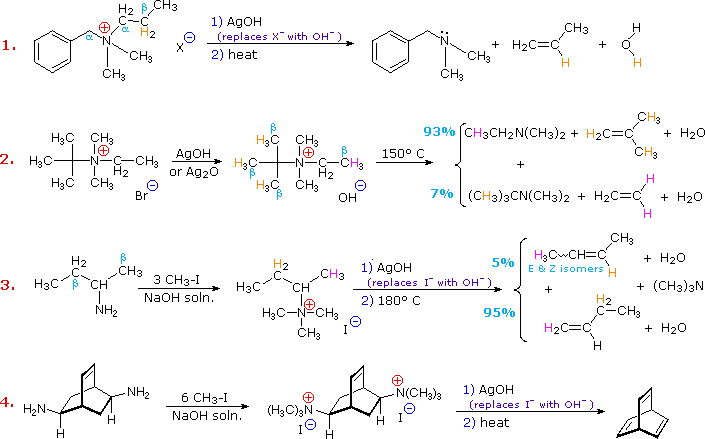
In example #2 above, two of the alkyl substituents on nitrogen have beta-hydrogens, all of which are on methyl groups (colored orange & magenta). The chief product from the elimination is the alkene having the more highly substituted double bond, reflecting not only the 3:1 numerical advantage of those beta-hydrogens, but also the greater stability of the double bond. Example #3 illustrates two important features of the Hofmann elimination:

1. Simple amines are easily converted to the necessary 4º-ammonium salts by exhaustive alkylation, usually with methyl iodide (methyl has no beta-hydrogens and cannot compete in the elimination reaction). Exhaustive methylation is shown again in example #4.
2. When a given alkyl group has two different sets of beta-hydrogens available to the elimination process (colored orange & magenta here), the major product is often the alkene isomer having the less substituted double bond.

The tendency of Hofmann eliminations to give the less-substituted double bond isomer is commonly referred to as the Hofmann Rule, and contrasts strikingly with the Zaitsev Rule formulated for dehydrohalogenations and dehydrations. In cases where other activating groups, such as phenyl or carbonyl, are present, the Hofmann Rule may not apply. Thus, if 2-amino-1-phenylpropane is treated in the manner of example #3, the product consists largely of 1-phenylpropene (E & Z-isomers).

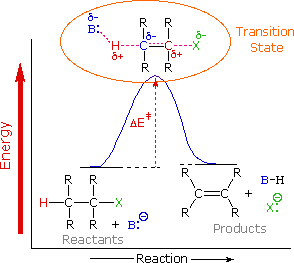
To understand why the base-induced elimination of 4º-ammonium salts behaves differently from that of alkyl halides it is necessary to reexamine the nature of the E2 transition state, first described for dehydrohalogenation. The energy diagram shown earlier for a single-step bimolecular E2 mechanism is repeated on the right. The E2 transition state is less well defined than is that of S_N2 reactions. More bonds are being broken and formed, with the possibility of a continuum of states in which the extent of C–H and C–X bond-breaking and C=C bond-making varies. For example, if the bond to the leaving group (X) is substantially broken relative to the other bond changes, the transition state approaches that for an E1 reaction (initial ionization followed by a fast second step). At the other extreme, if the acidity of the beta-hydrogens is enhanced, then substantial breaking of C–H may occur before the other bonds begin to be affected. For most simple alkyl halides it was proper to envision a balanced transition state, in which there was a synchronous change in all the bonds. Such a model was consistent with the Zaitsev Rule.

When the leaving group X carries a positive charge, as do the 4º-ammonium compounds discussed here, the inductive influence of this charge will increase the acidity of both the alpha and the beta-hydrogens. Furthermore, the 4º-ammonium substituent is much larger than a halide or hydroxyl group and may perturb the conformations available to substituted beta-carbons. It seems that a combination of these factors acts to favor base attack at the least substituted (least hindered and most acidic) set of beta-hydrogens. The favored anti orientation of the leaving group and beta-hydrogen, noted for dehydrohalogenation, is found for many Hofmann eliminations; but syn-elimination is also common, possibly because the attraction of opposite charges orients the hydroxide base near the 4º-ammonium leaving group.

Three additional examples of the Hofmann elimination are shown in the following diagram. Example #1 is interesting in two respects. First, it generates a 4º-ammonium halide salt in a manner different from exhaustive methylation. Second, this salt is not converted to its hydroxide analog prior to elimination. A concentrated aqueous solution of the halide salt is simply dropped into a refluxing sodium hydroxide solution, and the volatile hydrocarbon product is isolated by distillation.

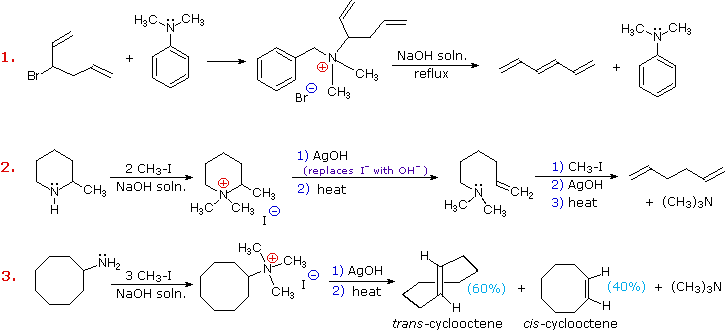
Example #2 illustrates an important aspect of the Hofmann elimination. If the nitrogen atom is part of a ring, then a single application of this elimination procedure does not remove the nitrogen as a separate 3º-amine product. In order to sever the nitrogen function from the molecule, a second Hofmann elimination must be carried out. Indeed, if the nitrogen atom was a member of two rings (fused or spiro), then three repetitions of the Hofmann elimination would be required to sever the nitrogen from the remaining molecular framework.

Example #3 is noteworthy because the less stable trans-cyclooctene is the chief product, accompanied by the cis-isomer. An anti-E2-transition state would necessarily give the cis-cycloalkene, so the trans-isomer must be generated by a syn-elimination. The cis-cyclooctene produced in this reaction could also be formed by a syn-elimination. Cyclooctane is a conformationally complex structure. Several puckered conformations that avoid angle strain are possible, and one of the most stable of these is shown on the right. Some eclipsed bonds occur in all these conformers, and transannular hydrogen crowding is unavoidable. Since the trimethylammonium substituent is large (about the size of tert-butyl) it will probably assume an equatorial-like orientation to avoid steric crowding. An anti-E2 transition state is likely to require an axial-like orientation of this bulky group, making this an unfavorable path.

Contributors

William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry