4.10: Chapter Solutions
- Page ID
- 191195
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Problem PP1.1.
a) With a shorter elution time, I has a higher molecular weight than II. The narrower peak means that I has a narrower dispersity than II.
b) With a shorter elution time, III has a higher molecular weight than IV. The wider peak means that III has a broader dispersity than IV.
c) With a higher elution time, V has a lower molecular weight than VI. The wider peak means that V has a broader dispersity than VI.
Problem PP1.2.
a) repeat unit: 109 x (C4H6O2) = 109 x 86.09 g/mol = 9,383.81 g/mol
end groups: C9H11 + Br = 119.19 + 79.9 = 199.09 g/mol
total: 9,383.81 + 199.09 = 9,582.90 g/mol
b) repeat unit: 763 x (C8H8) = 763 x 104.15 g/mol = 79,466.45 g/mol
end groups: C4H9 + H = 57.12 + 1.008 = 58.13 g/mol
total: 79,466.45 + 58.13 = 79,524.58 g/mol
c) repeat unit: 48 x (C4H6O2) = 48 x 86.09 g/mol = 4,132.32 g/mol
end groups: C4H9 + C7H5S2 = 57.12 + 153.26 = 210.38 g/mol
total: 4,132.32 + 210.38 = 4,342.70 g/mol
Problem PP1.3.
The ratio of the repeat unit integral per proton to the end group proton per integral gives the degree of polymerization. We could take the entire integration of the end group and divide it by the entire number of protons in that group, or select one position to represent the end group. Similarly, we can select one position to represent the repeat unit.
a) repeat unit integral per proton = 36.0 / 2H = 18
end group integral per proton = 0.32 / 2H = 0.16
degree of polymerization = 18/0.16 = 112
b) repeat unit integral per proton = 26.0 / 1H = 26
end group integral per proton = 1.32 / 9H = 0.15
degree of polymerization = 26/0.15 = 173
c) repeat unit integral per proton = 54.0 / 4H = 13.5
end group integral per proton = 0.49 / 1H = 0.49
degree of polymerization = 13.5/0.49 = 28
Problem PP2.1.
α is the slope, which is [rise]/[run]. That's approximately [4.0-2.4]/[6.6-4.4] = 1.6/2.2 = 0.73.
K is the y-intercept. The equation for a straight line is y = mx +b; in this case, y = 0.73x + b. If we choose a point on the line, such as (x,y) = (4.9, 2.0), we can substitute those values on for x and y to get b.
So 2.0 = 0.73(4.9) + b, or b = 2.0 - 3.56 = -1.56.
Problem PP2.2.
If the molecular weight is a million g/mol, then log(Mw) = 6. Interpolating, log([η]) = 4, or [η] = 10,000 ml/g.
Problem PP2.3.
If the intrinsic viscosity, [η] = 800 ml/g, then log([η]) = 2.9. Interpolating, log(Mw) = 5.1, or Mw = 126,000 g/mol.
Problem PP2.4.
Ethylene glycol can form hydrogen bonds at either end of the molecule, forming a supramolecular assembly much like a polymer. As a result, it has a much greater drag in solution, higher viscosity.
Problem PP3.1.
Honey is a concentrated solution of simple sugars, which are small molecules. Molasses, although similar to honey in some ways, also contain starches, which are polymers. This polymeric content leads to shear-thinning behavior.
Problem PP4.1.
a) There is a glass transition at around -18°C.
b) There is a melting point at around 125°C.
c) There is a glass transition at around -4°C.
d) There is a glass transition at around 117°C and a melting point at around 146°C.
Problem PP5.1.
a) Tg is observed at around 78°C, Tm is observed at around 117°C and Tc is observed at around 104°C.
b) Tg is observed at around 134°C and Tm is observed at around 167°C, but Tc is not observed; the sample failed to crystallize, but remained an amorphous solid.
c) Tm is observed at around 194°C and Tc is observed at around 187°C. Tg is not observed, and probably occurs below 150°C
d) Tg is observed at around 123°C, but Tm is not observed. The experiment checked much higher than Tg (over a hundred degrees), so the material may be an amorphous solid.
Problem PP6.1.
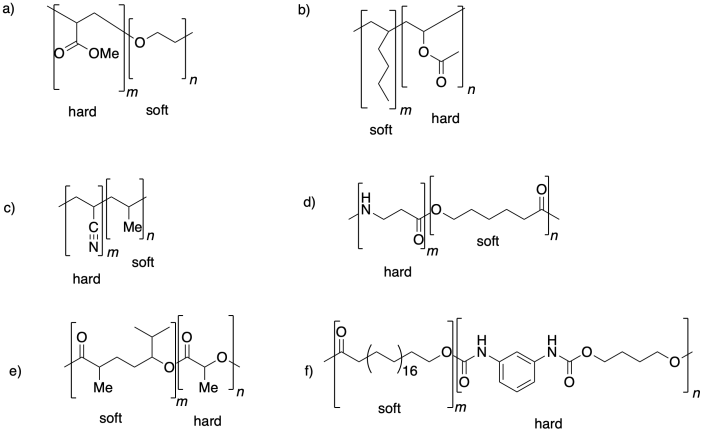
Problem PP6.2.
a) d = (2 x 3.14) / 0.40 = 16 Å; d = (2 x 3.14) / 0.70 = 9.0 Å
b) d = (2 x 3.14) / 0.25 = 25 Å; d = (2 x 3.14) / 0.85 = 7.4 Å
c) d = (2 x 3.14) / 0.25 = 25 Å; d = (2 x 3.14) / 0.52 = 12 Å; d = (2 x 3.14) / 0.66 = 10 Å
Problem PP7.1.
a) ultimate tensile strength = 800 Pa; strain at break = 55%
b) ultimate tensile strength = 750 Pa; strain at break = 215%
c) ultimate tensile strength = 220 Pa; strain at break = 120%
Problem PP7.2.
a) E = σ / ε = 180 Pa / 0.30 = 600 Pa
b) E = σ / ε = 450 Pa / 0.15 = 3,000 Pa
c) E = σ / ε = 50 Pa / 0.25 = 200 Pa
d) E = σ / ε = 75 Pa / 0.30 = 250 Pa
Problem PP7.3.
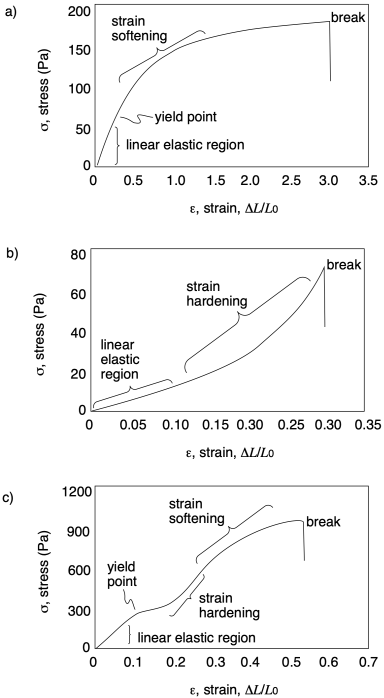
Problem PP8.1.
1 Pa = 1 Pa
1 kPa = 1,000 Pa
1 MPa = 1,000,000 Pa
1GPa = 1,000,000,000 Pa
Problem PP9.1.
a) glassy: storage modulus = 15 MPa; loss modulus = 70 kPa
rubbery: storage modulus = 7 MPa; loss modulus = 80 kPa
b) glassy: storage modulus = 600 kPa; loss modulus = 140 kPa
rubbery: storage modulus = 130 kPa; loss modulus = 150 kPa
c) glassy: storage modulus = 320 kPa; loss modulus = 80 kPa
rubbery: storage modulus = 70 kPa; loss modulus = 70 kPa
Problem PP9.2.
a) 89 °C
b) 170 °C
c) 124 °C