6.6: ¹H NMR Spectra and Interpretation (Part I)

Understanding the basics of NMR theory gets us ready to move on to the most important and practical part in this section, that is how to understand the 1H NMR spectrum and elucidate the structure of a compound from 1H NMR spectrum information. Let’s first take a look at an actual 1H NMR spectrum.

Fig. 6.6a The 1H NMR spectrum of methyl acetate

Generally, the information about the structure of molecule can be obtained from four aspects of a typical ¹H NMR spectrum:

• Chemical equivalent and non-equivalent protons (total number of signals)
• Chemical shift
• Integration
• Signal splitting

6.6.1 Chemical Equivalent and Non-Equivalent Protons

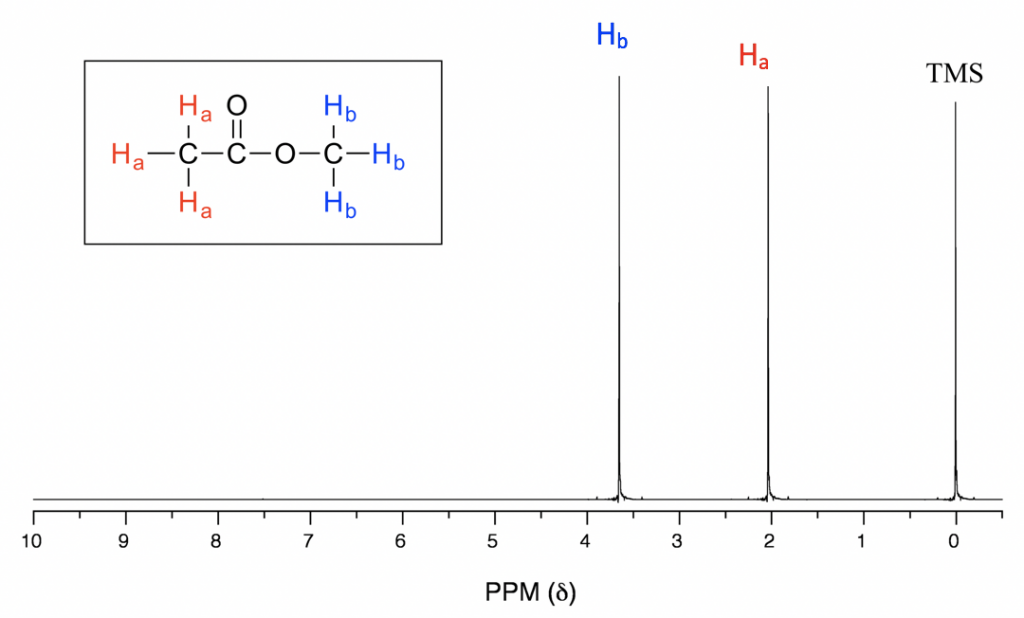
In the above ¹H NMR spectrum of methyl acetate (Fig. 6.6a), we can see that there are three signals. The peak at the far right is for the standard reference compound tetramethylsilane (TMS, more discussions in chemical shift section 6.6.2), not for the compound. So the compound methyl acetate shows two signals in ¹H NMR spectrum. Why only two signals for a compound containing total six hydrogens?

This is because of chemical equivalence. The total six hydrogens can be divided to two groups, the three H_a protons in the methyl group that bonded with C=O are all in the same chemical environment, therefore they are chemical equivalent. All chemical equivalent hydrogens have the same resonance frequency with applied to an external magnetic field, so show only one signal in ¹H NMR spectrum. The three H_b protons in the methyl group bonded with O atom are chemical equivalent as well and show the other signal. That is why there are total two signals for compound methyl acetate.

The ability to recognize chemical equivalent and non-equivalent protons in a molecule is very important in understanding NMR spectrum. For the compound with structure given, we should be able to predict how many signals are there in ¹H NMR spectrum. On the other side, if the ¹H NMR spectrum is available for an unknown compound, counting the number of signals in the spectrum tells us the number of different sets of protons in the molecule, and that is the very important information to determine the structure of the compound.

Here we will go through several examples for the first situation, that is to predict the number of signals in ¹H NMR spectrum with the structure of a compound given. To do that, we need to count how many distinct proton sets are included in the molecule.

For each of the following molecule, the chemically equivalent protons are labelled in the same color to facilitate the understanding.

• Benzene: all six protons are chemical equivalent (have the same bonding and in the same chemical environment) to each other and have the same resonance frequency in an ¹H NMR experiment, therefore show only one signal.
• Acetone: both methyl groups (two CH₃) bonded with C=O bond, so they are in the same chemical environment, and as a result all the six protons are chemical equivalent that show only one signal.

Notes: As you probably already realized, chemical equivalence or non-equivalence in NMR is closely related to symmetry. The protons that are symmetric to each other by a certain plane of symmetry are chemical equivalent.

The molecules in the next figure contains more sets of chemically equivalent protons.

• Acetaldehyde: The three H_a protons in the methyl group are chemical equivalent, and they all bonded to an sp³-hybridized carbon; but they are different to the H_b proton that is bonded to an sp²–hybridized carbonyl carbon. Two signals total in ¹H NMR spectrum.
• 1,4-dimethylbenzene: all four aromatic protons in are chemically equivalent because of the symmetry. The two methyl groups are equivalent to each other as well. Two signals total in ¹H NMR spectrum.
• 1,2-dimethylbenzene: both H_a protons are adjacent to a methyl substituent, while both H_c protons are two carbons away. So the four aromatic protons are divided to two sets. Both methyl groups are in the same bonding and symmetric to each other, they are equivalent. Three signals total in ¹H NMR spectrum.
• 1,3-dimethylbenzene: H_b is situated between two methyl groups, the two H_c protons are one carbon away from a methyl group, and H_d is two carbons away from a methyl group. Therefore, the four aromatic protons can be divided to three sets. The two methyl groups are equivalent. Four signals total in ¹H NMR spectrum.

Exercises 6.1

How many ¹H NMR signals would you predict for each of the following molecules?

Answers to Practice Questions Chapter 6

6.6.2 Chemical Shift

As seen in the ¹H NMR spectrum of methyl acetate (Fig. 6.6a), the x-axis units of NMR spectrum are in ppm (not in Hz as we would expect for frequency), and the two signals stand at different position along the x-axis. Let’s explain how that works and what information can be obtained.

The position of a signal along the x-axis of an NMR spectra is called chemical shift, or δ, of the signal. Chemical shift is determined by the structural electronical environment of the nuclei producing that signal. Protons in different chemical environments (non-equivalent) show signals at different chemical shift. The direction of chemical shift scale in x-axis is opposite to what we are familiar with, that is the smaller value is at right-hand side, and the larger value is at the left-hand side (Fig. 6.6b).

• Smaller chemical shift (δ) values correspond with lower resonance frequency;
• Larger chemical shift (δ) values correspond with higher resonance frequency.

By convention, the right-hand side of an NMR spectrum with smaller chemical shift values is called upfield, and the left-hand direction is called downfield (Fig. 6.6b).

Figure 6.6b The chemical shift scale in H NMR spectra

For protons that are shielded, because of the Blocal caused by circulating electrons, the magnetic field experienced by the proton, Beff, is smaller than applied external field, Bo, so the protons resonance at lower frequency and have smaller chemical shift values.

• Shielded protons have lower resonance frequency, and smaller chemical shift (d) values;
• Deshielded protons have higher resonance frequency, and larger chemical shift (d) values.

In 1H NMR spectrum, the absorption of the protons of TMS (tetramethylsilane) is defined as “zero” on the chemical shift (δ) scale, and the absorption of other protons are reported as relative shift compared with that of TMS.

TMS was chosen as a reference compound and defined as “zero” for several reasons. Since silicon is less electronegative than carbon, the hydrogens of TMS are in high electron-density environment, therefore are highly shielded with very low resonance frequency and rarely interfere with the signals of other compounds. Also there are twelve equivalent hydrogens in TMS that show a single signal, so the signal is rather strong even with very little amount of TMS. TMS is also quite inert and easy to be removed with the boiling point of 27 ºC. A small amount of TMS was used to be added in the sample as an internal standard for NMR measurement, and removed by evaporation afterwards. However, for contemporary NMR spectrometer (including the bench top NMR), it is no longer necessary to actually add TMS since the computer can calibrate the chemical shift electronically based on resonance frequencies of the solvent used.

The unit of chemical shift (δ) is ppm. The ‘ppm’ label stands for ‘parts per million’. The chemical shift relative to TMS in ppm is defined as the formula below.

The reason for using a relative value of chemical shift in ppm, rather than the actual resonance frequency in Hz is that every NMR instrument will have a different magnetic field strength, so the actual value of resonance frequencies expressed in Hz will be different on different instruments – remember that ΔE for the magnetic transition of a nucleus depends upon the strength of the externally applied magnetic field B_o. However, the chemical shift expressed in ppm will always be the same whether measured with an instrument operating at 400 MHz or 60 MHz. In the ¹H NMR of methyl acetate, the two signals are at 2.0 and 3.6 ppm represents the two sets of protons in methyl acetate have resonance frequencies about 2.0 and 3.6 parts per million higher than the resonance frequency of the TMS protons. If, for example, the spectrum is measured by the 400 MHz NMR spectrometer, then the chemical shift in Hz will be 800 Hz and 1440 Hz respectively.

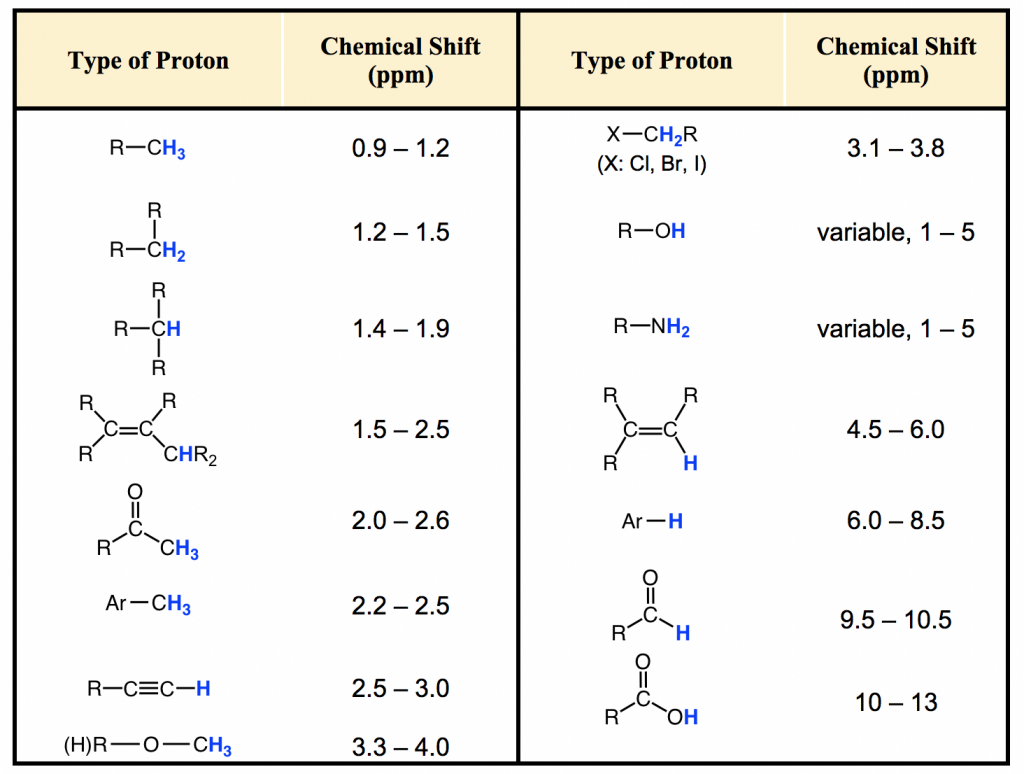
Most protons in organic compounds have chemical shift values between 0 and 12 ppm relative to TMS, although values below 0 ppm and above 12 ppm are occasionally observed. The chemical shift value of hydrogens in certain structural environment, or common organic functional groups, are listed in chart (Fig. 6.6c) and table (Table 6.2) below.

Figure 6.6c Chart of Approximate proton Chemical Shifts

Table 6.2: Approximate Proton Chemical Shifts of Common Functional Groups

The importance of chemical shift information is that it gives critical clues about molecular structures. Several highlights here:

• Usually the hydrogens in C-H bond, without any other functional groups nearby, are in the range of 1-2 ppm;
• For hydrogen in C-H bond beside double bond, like C=C or C=O bond, the signal goes downfield to 2-2.5 ppm;
• With electronegative atoms connected on the carbon, like O-C-H, the hydrogens get deshielded and chemical shift move further downfield to 3-4 ppm;
• The hydrogens bonded directly to double bond carbon have the chemical shift at around 4.5-6 pm;
• The aromatic hydrogens (H on benzene ring) show chemical shift around 7 ppm;
• The chemical shift of hydrogens in OH (alcohol) or NH (amine) group vary in a rather large range, from 1-5 ppm;
• The hydrogen in aldehyde (-CHO) and carboxylic acid (COOH) group has the chemical shift rather downfield at about 9-10 ppm and 10-12 ppm respectively.

When referring to the chemical shift table (or chart) for a certain compound, it is useful to keep in mind that the exact value may vary a bit to the given range, sometimes the difference up to 0.5 ppm unit may happen depends on the specific structure and the solvent used.

With chemical shift information available, we can now assign the signals in the ¹H NMR spectrum of methyl acetate. According to Fig. 6.6c, the protons in CH₃ group beside C=O bond are supposed to be in the range of 2-3 ppm, and protons in CH₃ group connected with O directly have δ value of about 3-4 ppm. So the 2.0 ppm signal is for the H_a group and 3.6 ppm signal is for H_b group.

Fig. 6.6d The 1H NMR spectrum of methyl acetate with signals assignment

Chemical Shift of Protons Near π Electrons — Anisotropy Effect

The chemical shift values of aromatic protons and vinylic protons (those directly bonded to an alkene carbon) resonate much further downfield (higher frequency, higher chemical shift) than can be accounted for simply by the deshielding effect of nearby electronegative atoms. These chemical shifts result from the anisotropy effect.

Let’s investigate the aromatic protons first. In benzene ring (and many other aromatic structures), the total six π electrons form delocalized big π bond around the ring (more discussions in Organic II). When the molecule is exposed to the external magnetic field B_o, these π electrons begin to circulate in a ring current and generating their own induced magnetic field B_induced. Whether shielding or deshielding occurs depends on the location of the protons in the induced magnetic field, and this is called anisotropy (means “non-uniformity”) effect. This can be illustrated specifically in the figure below by comparing between point A and B.

Figure 6.6e Anisotrophy effect of the induced magnetic field B(induced)

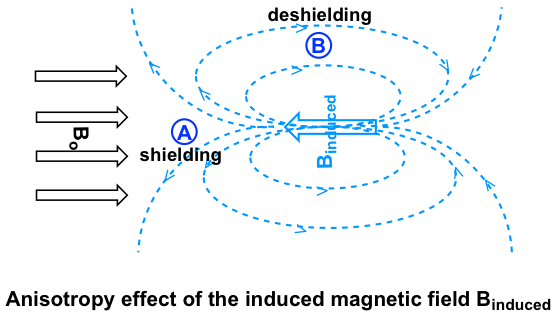
If a proton is at point A, it feels the induced magnetic field pointing to the opposes direction of B_o, sothe proton experiences shielding effect. For the proton at point B, however, it feels the induced magnetic field to the same direction as B_o, so the proton experiences deshielding effect.

The protons on benzene ring are at the position equivalent of ‘point B’, that means that the induced current in this region of space is oriented in the same direction as B₀, so it adds to B₀ and result in a deshilelding effect and the benzene protons resonance at a higher frequency and have larger chemical shifts.

Figure 6.6f Anisotrophy effect of Benzene ring: aromatic protons are at the location with deshielding effect, where the B(induced) is in the same direction as the B(O)

As a result, due to the anisotropy of the induced field generated by the circulating π electrons, the benzene protons are highly deshielded. Their chemical shift is far downfield, in the range of 6.5–8.5 ppm.

Anisotropy is also responsible for the downfield (high frequency) chemical shifts of vinylic protons (4–6.5 ppm) and aldehyde protons (9.5–11 ppm). The π electrons in these groups also circulate in such a way to generate an induced magnetic field that adds to external field B_o in the spots occupied by the protons. Carboxylic acid protons are even further downfield (9.5–12 ppm) due to the combined influence of the electronegative oxygen atom and the nearby π bond.

Figure 6.6g Anisotrophy Effect of Alkene: Vinylic protons are at the location with deshielding effect, where the Binduced is in the same direction as the Bo