29.5: Cycloaddition Reactions

A concerted combination of two π-electron systems to form a ring of atoms having two new σ bonds and two fewer π bonds is called a cycloaddition reaction. The number of participating π-electrons in each component is given in brackets preceding the name of the reaction. The Diels-Alder reaction (Section 14-4) is the most useful cycloaddition reaction due to the ubiquity of 6-membered rings and its ability to reliably control stereochemistry in the product. In the Diels-Alder cycloaddition reaction, a conjugated diene, simply referred to as the diene, reacts with a double or triple bond coreactant called the dienophile, because it combines with (has an affinity for) the diene. The Diels-Alder reaction is a [4+2] cycloaddition (4 pi electrons from the diene and 2 pi electrons from the dienophile) that yields a functionalized 6-membered ring product. During the Diels-Alder reaction, two pi-bonds are converted to two sigma-bonds.

Due to the concerted mechanism for cycloaddition reactions, the geometry of atoms on the dienophile or the diene maintain their orientation in the product. This is a critical point for the 4 atoms (both dienophile atoms and the terminal atoms of the diene) that become sp³ hybridized and thus are potential stereocenters in the product. (As a reminder, when chiral products are formed, we obtain a racemic mixture of enantiomers.) As highlighted below, cis dienophiles yield cis substituents in the product, while trans dienophiles yield trans product substituents. Substituents on the terminal atoms of the diene also can become stereocenters and this analysis is a little less straightforward than for dienophile substituents. The way to think about the diene substituents is whether the are pointing "outside" or "inside" the diene. These orientations are illustrated below. When groups are both pointing "outside" or "inside", we can consider them to be cis and they will end up cis in the product. When one group is pointing "outside" and one "inside", we can consider them as trans and they will be trans in the product.

Another important reaction is the [2+2] cycloaddition of two alkene containing molecules to form a 4-membered cyclobutane ring. The [2 + 2] cycloaddition of two alkenes does not occur by simply heating but can only be achieved by irradiation with ultraviolet light.

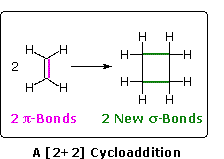
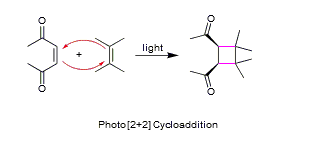
Many other cycloadditions are known, such as [2 + 2 + 2], and other types of [2 + 2], which give different size of rings. Some specific examples are shown below:

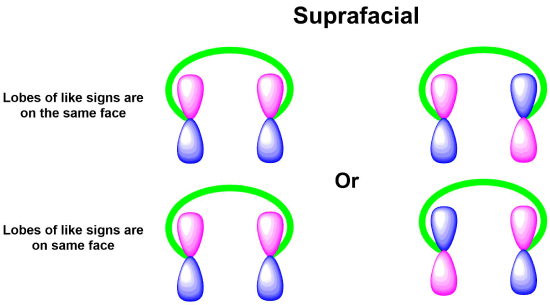
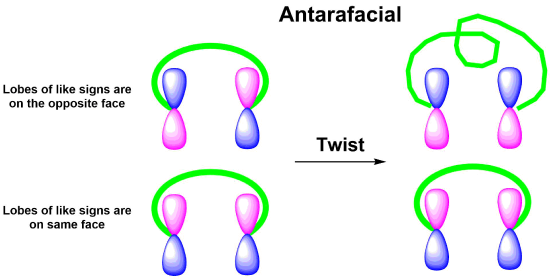
Like other pericyclic reactions, cycloadditions are determined by the orbital symmetry of the frontier orbitals of the reactants. For bonding to occur in a cycloaddition, the terminal lobes of the frontier orbitals of the two pi systems must have the correct symmetry. Correct symmetry can be obtained in two different ways. If the signs on the orbital lobes are the same on the faces of both reactants then the reaction undergoes a suprafacial cycloaddition. If the signs of the orbital lobes are the same on the face of one reactant but opposite on the other reactant then the reaction undergoes an antarafacial cycloaddition. Although both types are symmetry allowed, the fact that antarafacial cycloadditions require the twisting of a pi orbital system makes them more difficult to achieve.