8.3: The Alkene Double Bond and Stereoisomerism
- Page ID
- 45188
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objective
- recognize and classify the stereochemistry of alkenes using the cis/trans system
Steroisomerism in Alkenes
There is free rotation about the carbon-to-carbon single bonds (C–C) in alkanes. For example, in 1,2-dichloroethane, there is free rotation about the C–C bond. The two models shown represent exactly the same molecule; they are not isomers. You can draw structural formulas that look different, but if you bear in mind the possibility of this free rotation about single bonds, you should recognize that these two structures represent the same molecule:

In contrast, the structure of alkenes requires that the carbon atoms of a double bond and the two atoms bonded to each carbon atom all lie in a single plane, and that each doubly bonded carbon atom lies in the center of a triangle. This part of the molecule’s structure is rigid; rotation about doubly bonded carbon atoms is not possible without rupturing the bond. In 1,2-dichloroethene, restricted rotation about the double bond means that the relative positions of substituent groups above or below the double bond become significant. This leads to a special kind of isomerism. The isomer in which the two chlorine (Cl) atoms lie on the same side of the molecule is called the cis isomer (Latin cis, meaning “on this side”) and is named cis-1,2-dichloroethene. The isomer with the two Cl atoms on opposite sides of the molecule is the trans isomer (Latin trans, meaning “across”) and is named trans-1,2-dichloroethene. These two compounds are cis-trans isomers (or geometric isomers), compounds that have different configurations (groups permanently in different places in space) because of the presence of a rigid structure in their molecule.

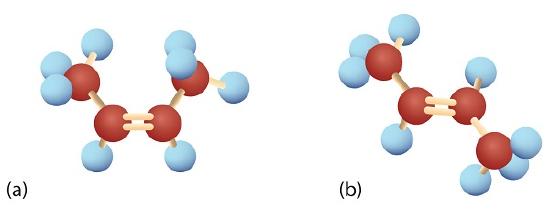
The diagram below summarizes the differences between alkanes and alkenes with respect to rotation where the carbons are red, hydrogens are off-white, and the chlorines are green.

In 1,2-dichloroethane (a), free rotation about the C–C bond allows the two structures to be interconverted by a twist of one end relative to the other. In 1,2-dichloroethene (b), restricted rotation about the double bond means that the relative positions of substituent groups above or below the double bond are significant.
Geometric Isomers have Different Physical Properties
Consider the alkene with the condensed structural formula CH3CH=CHCH3. We could name it 2-butene, but there are actually two such compounds; the double bond results in cis-trans isomerism. Cis-2-butene has both methyl groups on the same side of the molecule. Trans-2-butene has the methyl groups on opposite sides of the molecule as shown in the diagram below.
Cis-2-butene and trans-2-butene are unique compounds with slightly different physical properties as shown below. For stereospecific reactions, these compounds produce different stereoisomeric products under the same reaction conditions. This phenonenom of reactivity will be explored more closely in the next chapter on alkene reactivity.

Example
Which compounds can exist as cis-trans (geometric) isomers? Draw them.
- CHCl=CHBr
- CH2=CBrCH3
- (CH3)2C=CHCH2CH3
- CH3CH=CHCH2CH3
Solutions Explained
All four structures have a double bond and thus meet rule 1 for cis-trans isomerism.
- This compound meets rule 2; it has two nonidentical groups on each carbon atom (H and Cl on one and H and Br on the other). It exists as both cis and trans isomers:

- This compound has two hydrogen atoms on one of its doubly bonded carbon atoms; it fails rule 2 and does not exist as cis and trans isomers.
- This compound has two methyl (CH3) groups on one of its doubly bonded carbon atoms. It fails rule 2 and does not exist as cis and trans isomers.
- This compound meets rule 2; it has two nonidentical groups on each carbon atom and exists as both cis and trans isomers:

Exercise
Exercise
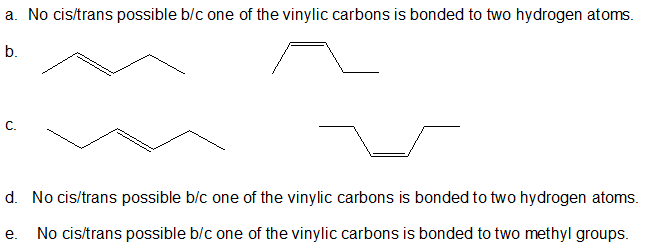
1. If the compound below can exist as cis-trans isomers, then draw both bond-line structures.
- CH2=CHCH2CH2CH3
- CH3CH=CHCH2CH3
- CH3CH2CH=CHCH2CH3
- CH2C(CH3)CH2CH3
- CH3C(CH3)CHCH3
2. Write out the condensed structure for ethene.
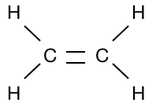
3. Draw the Kekulé (Lewis) structure for ethene.
4. Draw the bond-line structure for ethene.
5. Why is it that the carbons in ethene cannot freely rotate around the carbon-carbon double bond?
- Answer
- 1.
-
2. CH2CH2 The carbon-carbon double bond is not shown, but can be recognized by knowing the neutral bonding patterns of carbon.
3.
4." - " Note how easy it would be to misinterpret this small dash, therefore, the structure for ethene is typically shown with a condensed or Kekule structure.
5. The carbons cannot freely rotate about the carbon-carbon double bond because rotating p-orbitals would have to pass through a 90° point where there would no longer be any overlap, so the \(\pi\) bond would have to break for there to be free rotation.

