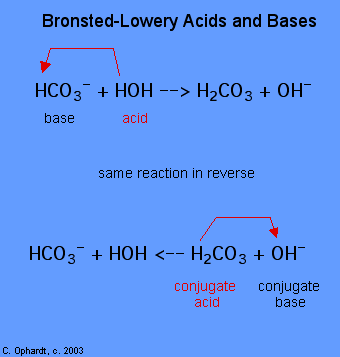2.3: Acids and Bases; Electrophiles and Nucleophiles
- Page ID
- 32331
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Brønsted-Lowry definition of acidity
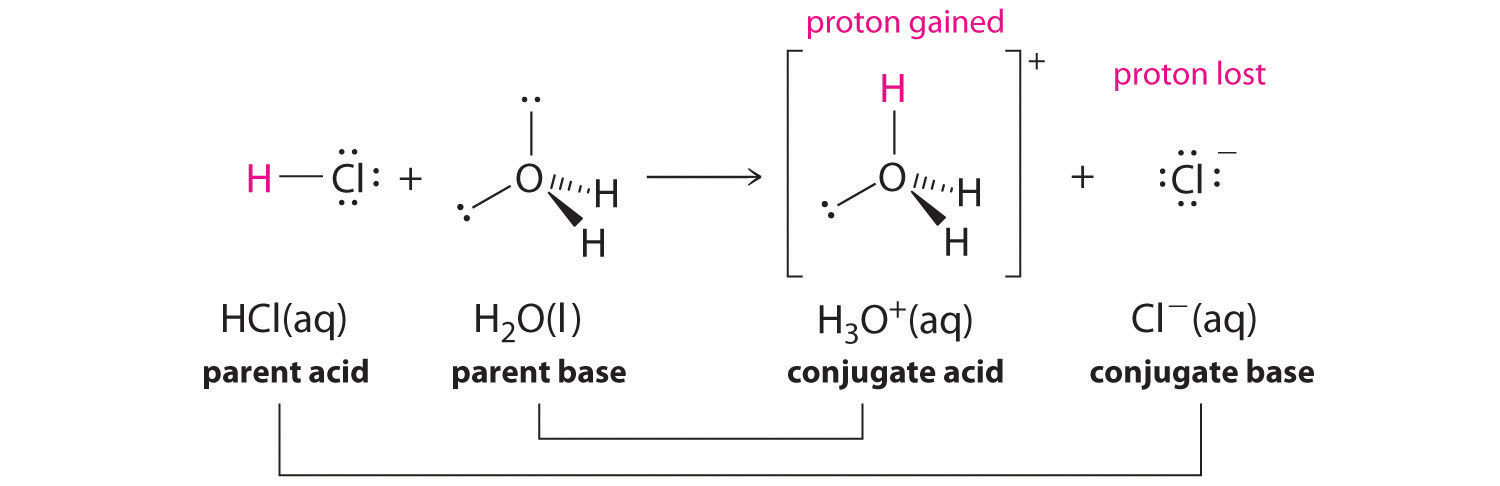
We’ll begin our discussion of acid-base chemistry with a couple of essential definitions. The first of these definitions was proposed in 1923 by the Danish chemist Johannes Brønsted and the English chemist Thomas Lowry, and has come to be known as the Brønsted-Lowry definition of acids and bases. An acid, by the Brønsted-Lowry definition, is a species which is able to donate a proton (H+), while a base is a proton acceptor. We have already discussed in the previous chapter one of the most familiar examples of a Brønsted-Lowry acid-base reaction, between hydrochloric acid and hydroxide ion:

In this reaction, a proton is transferred from HCl (the acid, or proton donor) to hydroxide (the base, or proton acceptor). As we learned in the previous chapter, curved arrows depict the movement of electrons in this bond-breaking and bond-forming process.
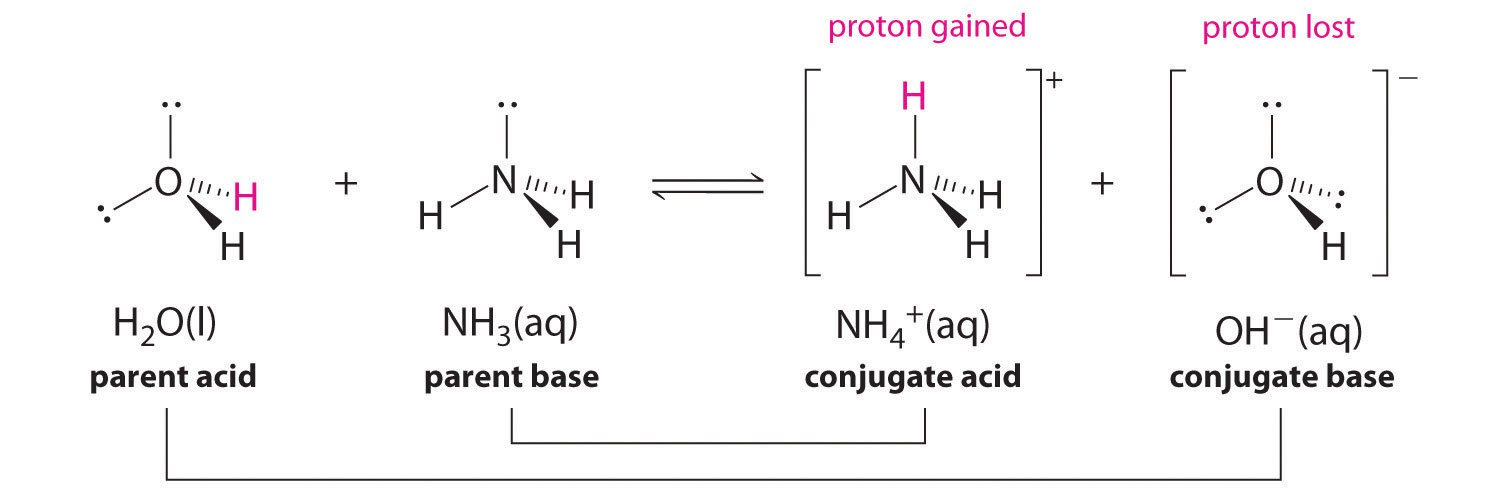
After a Brønsted-Lowry acid donates a proton, what remains – in this case, a chloride ion – is called the conjugate base. Chloride is thus the conjugate base of hydrochloric acid. Conversely, when a Brønsted-Lowry base accepts a proton it is converted into its conjugate acid form: water is thus the conjugate acid of hydroxide.
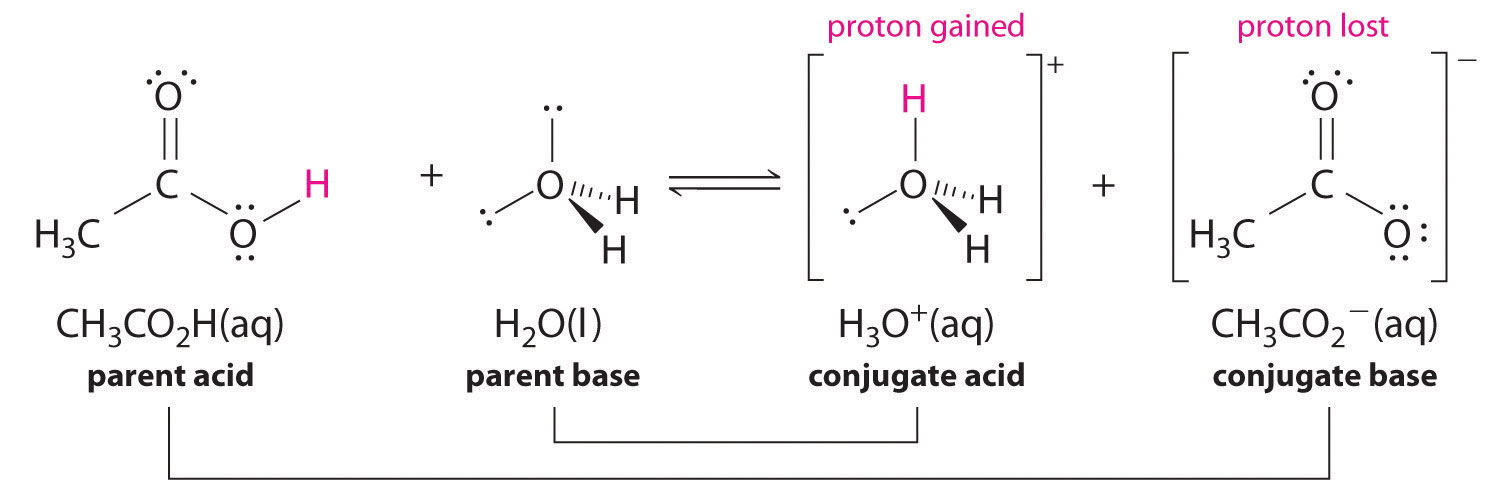
We can also talk about conjugate acid/base pairs: the two acid/base pairs involved in our first reaction are hydrochloric acid/chloride and hydroxide/water. In this next acid-base reaction, the two pairs involved are acetate/acetic acid and methyl ammonium/methylamine:
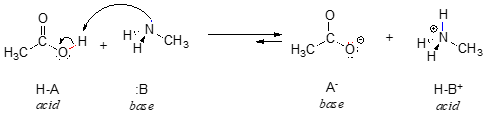
Throughout this text, we will often use the abbreviations HA and :B in order to refer in a general way to acidic and basic reactants:
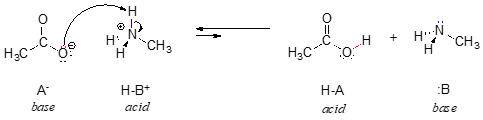
In order to act as a proton acceptor, a base must have a reactive pair of electrons. In all of the examples we shall see in this chapter, this pair of electrons is a non-bonding lone pair, usually (but not always) on an oxygen, nitrogen, sulfur, or halogen atom. When acetate acts as a base in the reaction shown above, for example, one of its oxygen lone pairs is used to form a new bond to a proton. The same can be said for an amine acting as a base. Clearly, methyl ammonium ion cannot act as a base – it does not have a reactive pair of electrons with which to accept a new bond to a proton.
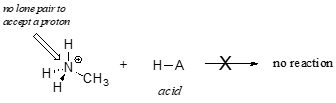
Later, in chapter 15, we will see several examples where the (relatively) reactive pair of electrons in a \( \pi \) bond act in a basic fashion.
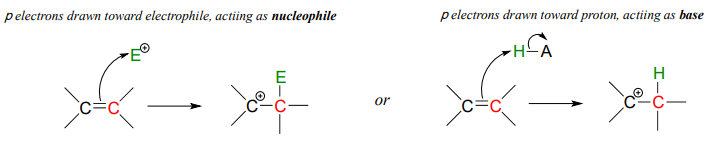
In this chapter, we will concentrate on those bases with non-bonding (lone pair) electrons.
| Example |
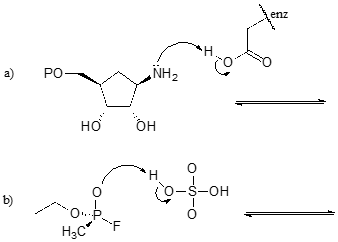
Exercise 7.1: Draw structures for the missing conjugate acids or conjugate bases in the reactions below.
Contributors
- Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)
You are no doubt aware that some acids are stronger than others. Sulfuric acid is strong enough to be used as a drain cleaner, as it will rapidly dissolve clogs of hair and other organic material.
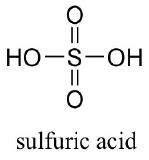
Not surprisingly, concentrated sulfuric acid will also cause painful burns if it touches your skin, and permanent damage if it gets in your eyes (there’s a good reason for those safety goggles you wear in chemistry lab!). Acetic acid (vinegar), will also burn your skin and eyes, but is not nearly strong enough to make an effective drain cleaner. Water, which we know can act as a proton donor, is obviously not a very strong acid. Even hydroxide ion could theoretically act as an acid – it has, after all, a proton to donate – but this is not a reaction that we would normally consider to be relevant in anything but the most extreme conditions.
The relative acidity of different compounds or functional groups – in other words, their relative capacity to donate a proton to a common base under identical conditions – is quantified by a number called the dissociation constant, abbreviated Ka. The common base chosen for comparison is water.
We will consider acetic acid as our first example. When a small amount of acetic acid is added to water, a proton-transfer event (acid-base reaction) occurs to some extent.
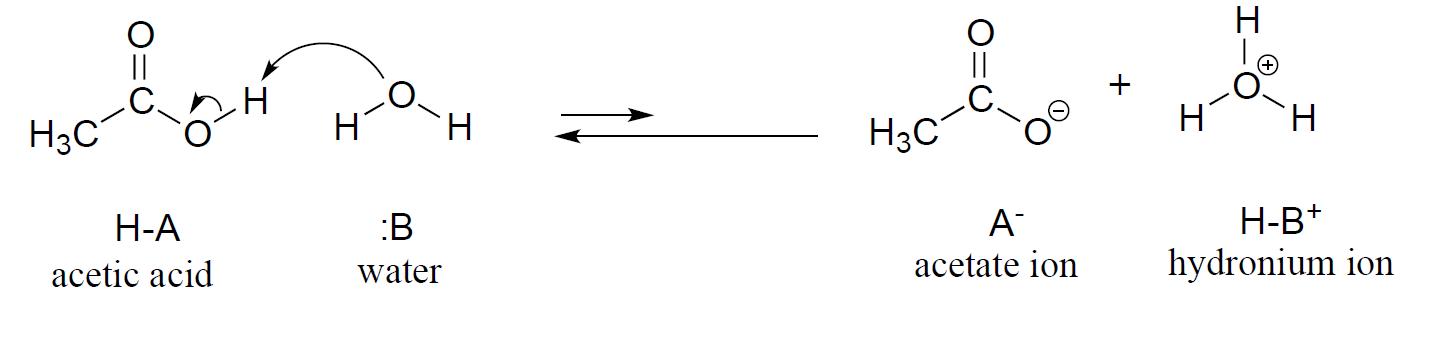
Notice the phrase ‘to some extent’ – this reaction does not run to completion, with all of the acetic acid converted to acetate, its conjugate base. Rather, a dynamic equilibrium is reached, with proton transfer going in both directions (thus the two-way arrows) and finite concentrations of all four species in play. The nature of this equilibrium situation, as you recall from General Chemistry, is expressed by an equilibrium constant, Keq. The equilibrium constant is actually a ratio of activities (represented by the symbol \(a\)), but activities are rarely used in courses other than analytical or physical chemistry. To simplify the discussion for general chemistry and organic chemistry courses, the activities of all of the solutes are replaced with molarities, and the activity of the solvent (usually water) is defined as having the value of 1.
In our example, we added a small amount of acetic acid to a large amount of water: water is the solvent for this reaction. Therefore, in the course of the reaction, the concentration of water changes very little, and the water can be treated as a pure solvent, which is always assigned an activity of 1. The acetic acid, acetate ion and hydronium ion are all solutes, and so their activities are approximated with molarities. The acid dissociation constant, or Ka, for acetic acid is therefore defined as:
\[ K_{eq} = \dfrac{a_{CH_3COO^-}·a_{H_3O^+}}{a_{CH_3COOH}·a_{H_2O}} ≈ \dfrac{[CH_3COO^-][H_3O^+]}{[CH_3COOH][1]}\]
Because dividing by 1 does not change the value of the constant, the "1" is usually not written, and Ka is written as:
\[ K_{eq} = K_{a} = \dfrac{[CH_3COO^-][H_3O^+]}{[CH_3COOH]} = 1.75 \times 10^{-5}\]
In more general terms, the dissociation constant for a given acid is expressed as:
\[ K_a = \dfrac{[A^-][H_3O^+]}{[HA]} \label{First}\]
or
\[ K_a = \dfrac{[A][H_3O^+]}{[HA^+]} \label{Second}\]
The first expression applies to a neutral acid such as like HCl or acetic acid, while the second applies to a cationic acid like ammonium (NH4+).
The value of Ka = 1.75 x 10-5 for acetic acid is very small - this means that very little dissociation actually takes place, and there is much more acetic acid in solution at equilibrium than there is acetate ion. Acetic acid is a relatively weak acid, at least when compared to sulfuric acid (Ka = 109) or hydrochloric acid (Ka = 107), both of which undergo essentially complete dissociation in water.
A number like 1.75 x 10- 5 is not very easy either to say or to remember. Chemists have therefore come up with a more convenient term to express relative acidity: the pKa value.
pKa = -log Ka
Doing the math, we find that the pKa of acetic acid is 4.8. The use of pKa values allows us to express the acidity of common compounds and functional groups on a numerical scale of about –10 (very strong acid) to 50 (not acidic at all). Table 7 at the end of the text lists exact or approximate pKa values for different types of protons that you are likely to encounter in your study of organic and biological chemistry. Looking at Table 7, you see that the pKa of carboxylic acids are in the 4-5 range, the pKa of sulfuric acid is –10, and the pKa of water is 14. Alkenes and alkanes, which are not acidic at all, have pKa values above 30. The lower the pKa value, the stronger the acid.
It is important to realize that pKa is not at all the same thing as pH: the former is an inherent property of a compound or functional group, while the latter is the measure of the hydronium ion concentration in a particular aqueous solution:
pH = -log [H3O+]
Any particular acid will always have the same pKa (assuming that we are talking about an aqueous solution at room temperature) but different aqueous solutions of the acid could have different pH values, depending on how much acid is added to how much water.
Our table of pKa values will also allow us to compare the strengths of different bases by comparing the pKavalues of their conjugate acids. The key idea to remember is this: the stronger the conjugate acid, the weaker the conjugate base. Sulfuric acid is the strongest acid on our list with a pKa value of –10, so HSO4- is the weakest conjugate base. You can see that hydroxide ion is a stronger base than ammonia (NH3), because ammonium (NH4+, pKa = 9.2) is a stronger acid than water (pKa = 14.0).
While Table 7 provides the pKa values of only a limited number of compounds, it can be very useful as a starting point for estimating the acidity or basicity of just about any organic molecule. Here is where your familiarity with organic functional groups will come in very handy. What, for example, is the pKaof cyclohexanol? It is not on the table, but as it is an alcohol it is probably somewhere near that of ethanol (pKa = 16). Likewise, we can use Table 7 to predict that para-hydroxyphenyl acetaldehyde, an intermediate compound in the biosynthesis of morphine, has a pKa in the neighborhood of 10, close to that of our reference compound, phenol.
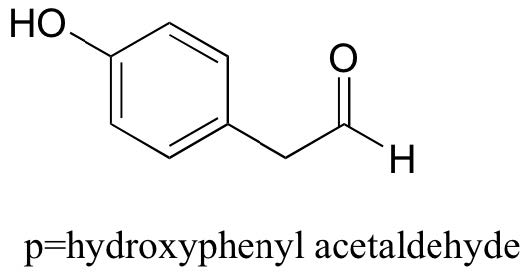
Notice in this example that we need to evaluate the potential acidity at four different locations on the molecule.
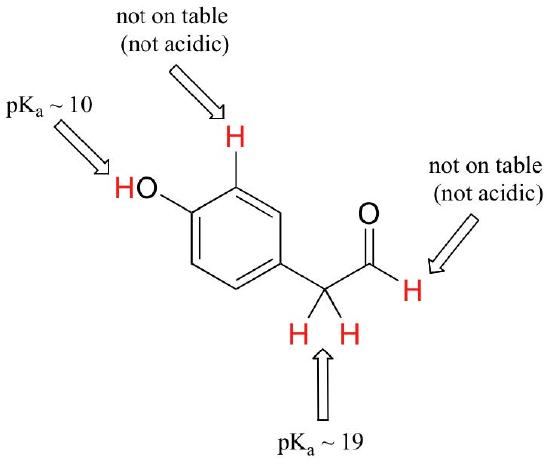
Aldehyde and aromatic protons are not at all acidic (pKavalues are above 40 – not on our table). The two protons on the carbon next to the carbonyl are slightly acidic, with pKa values around 19-20 according to the table. The most acidic proton is on the phenol group, so if the compound were to be subjected to a single molar equivalent of strong base, this is the proton that would be donated.
As you continue your study of organic chemistry, it will be a very good idea to commit to memory the approximate pKa ranges of some important functional groups, including water, alcohols, phenols, ammonium, thiols, phosphates, carboxylic acids and carbons next to carbonyl groups (so-called a-carbons). These are the groups that you are most likely to see acting as acids or bases in biological organic reactions.
A word of caution: when using the pKa table, be absolutely sure that you are considering the correct conjugate acid/base pair. If you are asked to say something about the basicity of ammonia (NH3) compared to that of ethoxide ion (CH3CH2O-), for example, the relevant pKa values to consider are 9.2 (the pKa of ammonium ion) and 16 (the pKa of ethanol). From these numbers, you know that ethoxide is the stronger base. Do not make the mistake of using the pKa value of 38: this is the pKa of ammonia acting as an acid, and tells you how basic the NH2- ion is (very basic!)
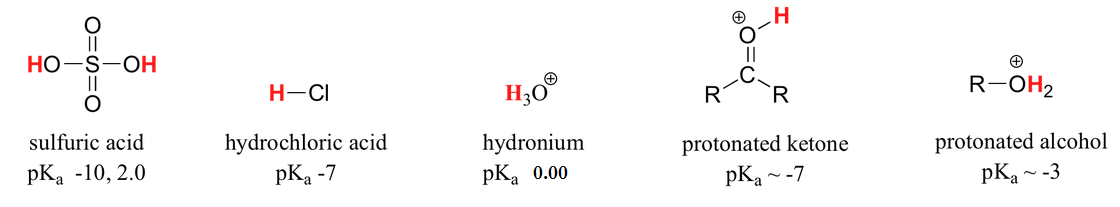

| Example |
|---|
|
Exercise 7.2: Using the pKa table, estimate pKa values for the most acidic group on the compounds below, and draw the structure of the conjugate base that results when this group donates a proton. |