Chapter 7 Solutions
- Page ID
- 1122
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)P7.1:
The interior Asp has a higher pKa (is less acidic). It is in a hydrophobic environment, meaning that that the charged (aspartate) form of the side chain will be highly destabilized relative to the uncharged aspartic acid form.
P7.2:
In all cases the pKa of the amino acid side chain (or of water, for part e) is expected to be lower due to the proximity of the cationic magnesium ion. The positive charge on the metal ion is expected to stabilize the negatively-charged conjugate base form of Glu, Tyr, and water, and to destabilize the positively charged, conjugate acid forms of Lys and His.
P7.3:
a) The base on the right is stronger
b) The base on the left is stronger
c) The base on the left is stronger
d) The base on the right is stronger
e) The base on the left is stronger
f) The base on the right is stronger
g) The base on the right is stronger
h) The base on the right is stronger
i) The base on the left is stronger
j) The base on the left is stronger
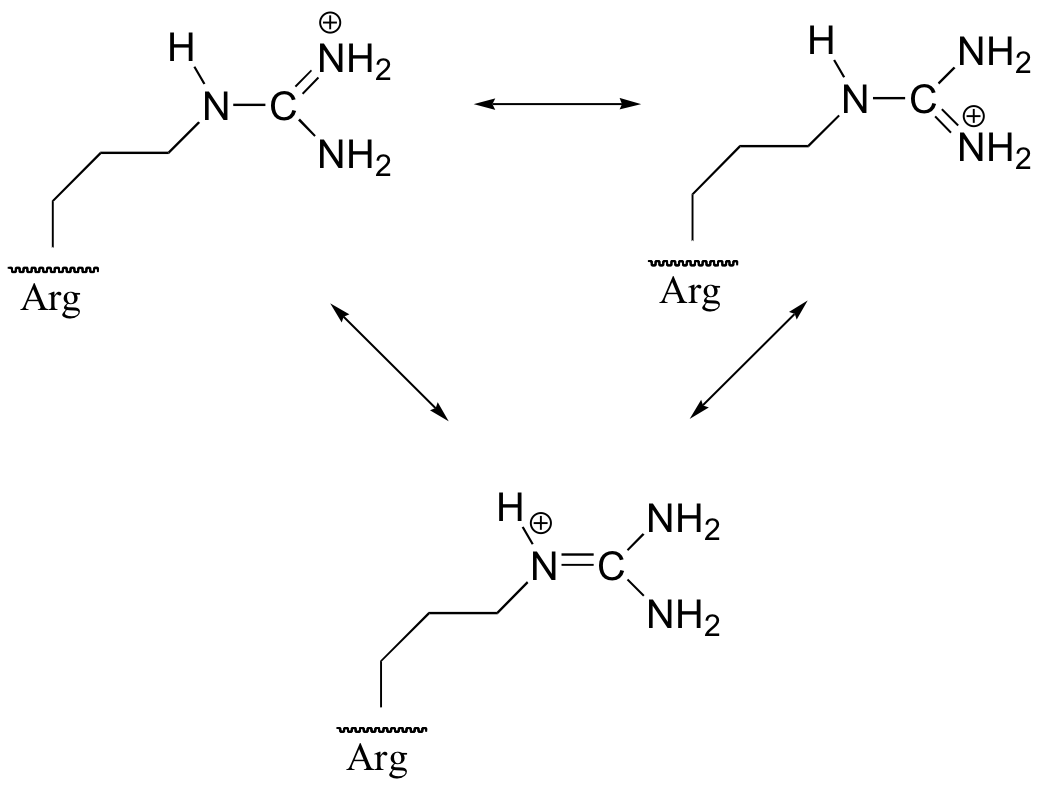
P7.4: The positive charge on the protonated form of arginine can be delocalized by resonance to all three of the nitrogens – this stabilizes the conjugate acid form (ie. makes it a weaker acid). On the protonated form of lysine, by contrast, the positive charge is ‘stuck’ on the single nitrogen (see the structure of lysine in chapter 6). Because the positive charge of of lysine is not stabilized by resonance, lysine is more likely to give up a proton and lose the charge.
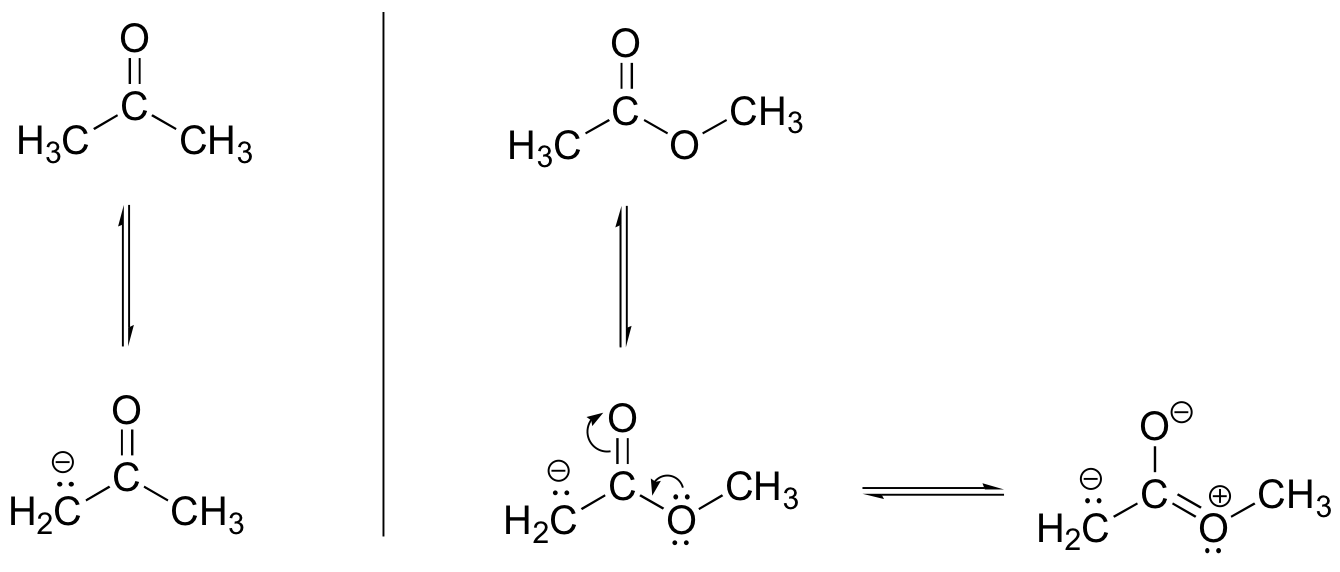
P7.5: The ester oxygen acts as an electron-donating group by resonance. This electron-donating property destabilizes the negative charge on the enolate form, making the a-proton less acidic. This argument also holds true for thioesters.
P7.6:
a) The most acidic proton on tetracycline is indicated below. Notice that the negative charge on the conjugate base can be delocalized to two carbonyl oxygens.
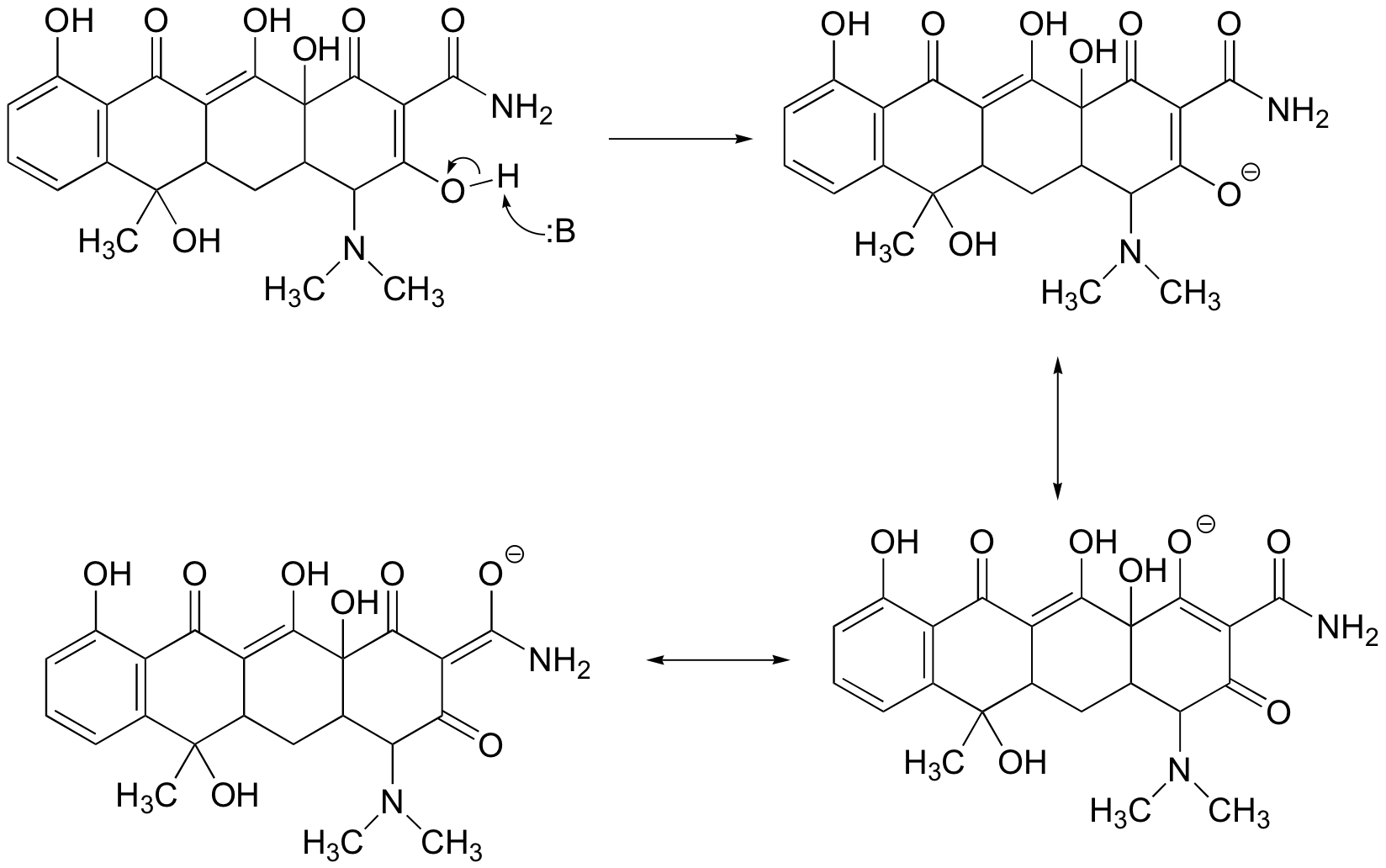
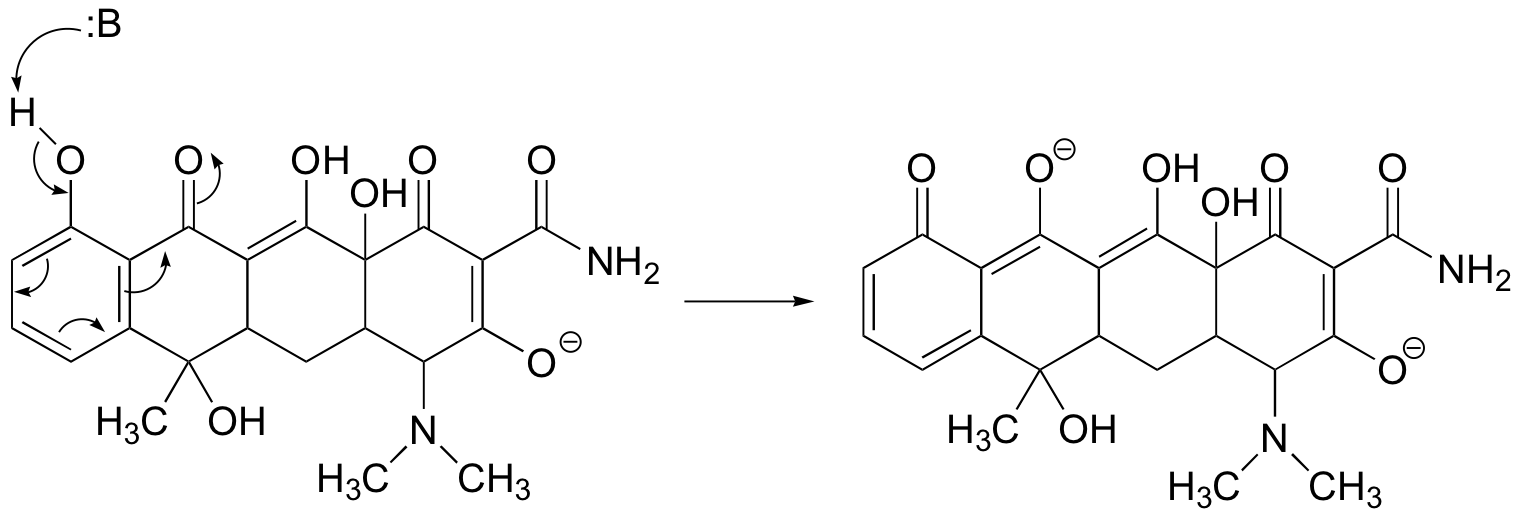
When the second most acidic proton is abstracted by a base, the resulting negative charge can be delocalized to one carbonyl oxygen (in addition to three aromatic carbons). The 2nd conjugate base of tetracycline is shown below (having fully reacted with two molar equivalents of strong base).
P7.7:

fig 5
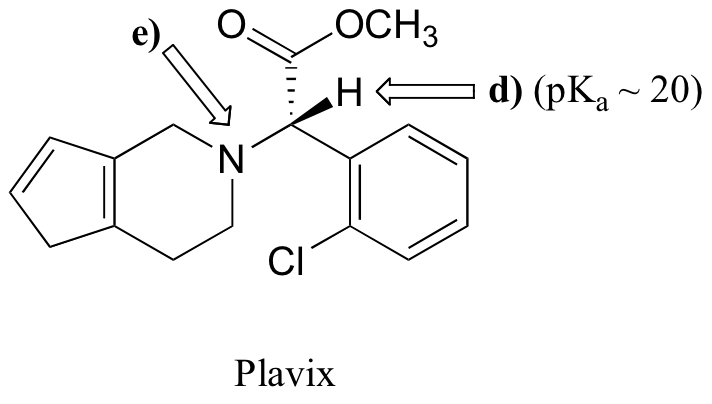
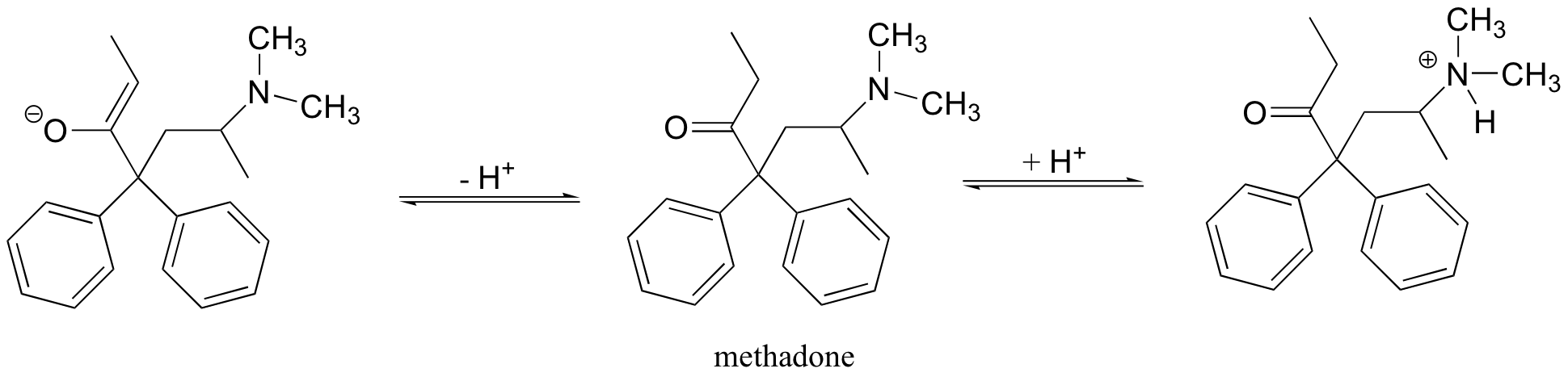
P7.8:
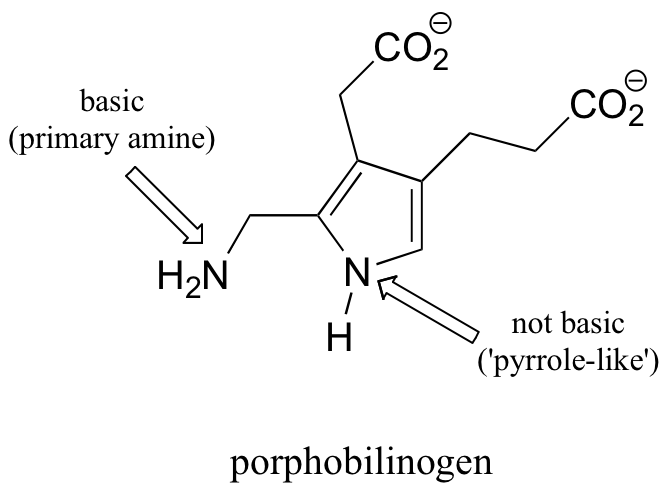
P7.9: One nitrogen is simply a primary amine, and as such is basic. The other nitrogen is ‘pyrrole-like’, meaning that its lone pair is part of an aromatic sextet, and is not available for bonding to another proton.
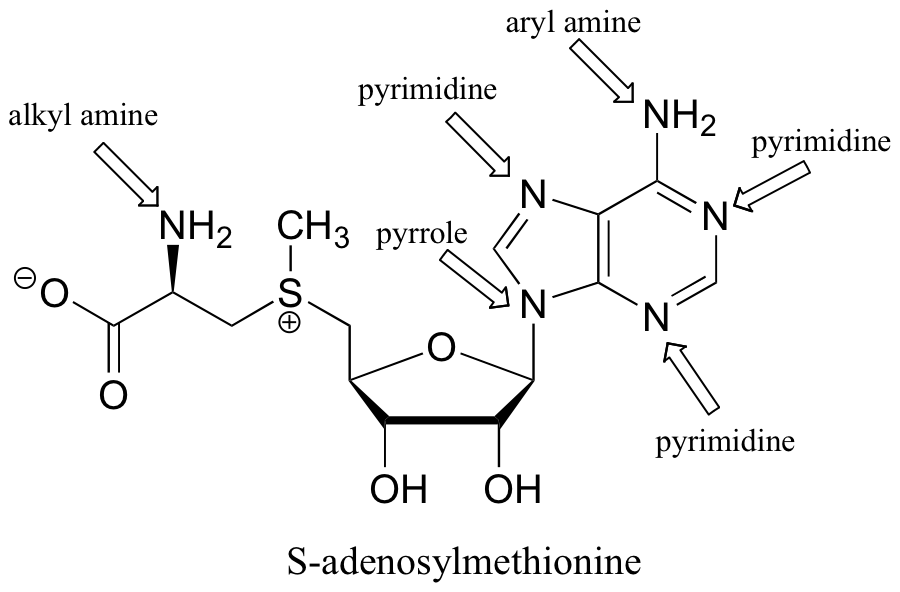
P7.10: The alkyl amine nitrogen is most basic, the ‘pyrrole-like’ nitrogen is least basic.
P7.11:
Proton Ha is more acidic. The negative charge on the conjugate base that results from the abstraction of Ha can be delocalized to both oxygens plus a carbon, whereas the negative charge from abstraction of Hb can be delocalized just to the two oxygens.
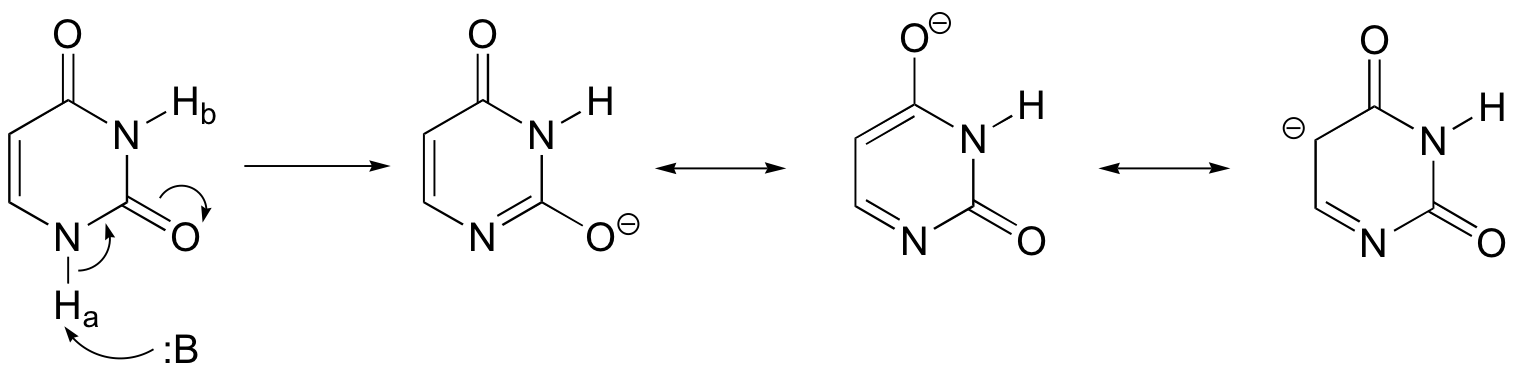
P7.12:
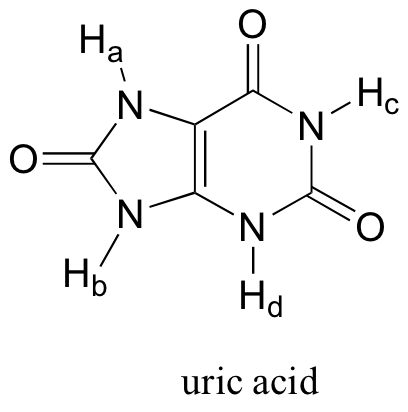
Of the four protons, Ha is the least acidic. The negative charge that results from abstraction of Ha can be delocalized to only one oxygen atom, whereas the charge resulting from abstraction of either Hb, Hc, and Hd can be delocalized to two oxygens in each case.
P7.13: The total charge will be very close to –3.0. At pH = 7.3, the N-terminus proline (pKa = 10.6) will be fully protonated, and will contribute a charge of +1. This is balanced, however, by a negative charge on the terminal glutamate (pKa = 2.2). Three of the seven amino acids in the peptide have ionizable side chains: an aspartate (D) and two glutamates (E). The pKa values for these side chains are 3.7 and 4.3, respectively, so at pH 7 all three will be fully ionized, leading to a total peptide charge of –3.
P7.14: There are three ionizable groups on this peptide: the terminal amino group on Asp (pKa ~ 9.6), the side-chain carboxylate group on Asp (pKa ~ 3.7) and the terminal carboxylate on Ile (pKa ~ 2.4). For each buffer, we can use the Henderson-Hasselbalch equation to determine the charged / uncharged ratio for each group.
a) At pH = 4.0:
Asp (terminal amino) [HA+] / [A] = 10(9.6-4.0) = 105.6 = 4.0 x 105. At this pH the terminal amino group is essentially 100% protonated and positively charged, so this group contributes a charge of +1.
Asp (side chain): [HA] / [A-] = 10(3.7 - 4.0) = 10(-0.3) = 0.50. Approximately 2 out of every 3 side chains is deprotonated and negatively charged, so overall this group contributes a charge of -0.67.
Ile (terminal carboxylate): ): [HA] / [A-] = 10(2.4 - 4.0) = 10(-1.6) = 0.025. Most, but not all of the terminal carboxylates are deprotonated and negatively charged. We can calculate the percentage that are protonated:
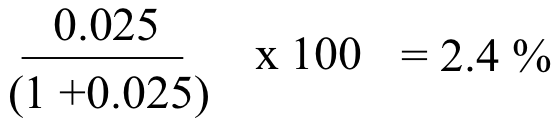
. . .thus about 97.6% are deprotonated and negatively charged. This group contributes an overall charge of -0.98.
In a buffer of pH 4.0, the total charge on the dipeptide will be:
(+1) + (-0.67) + (-0.98) = -0.65.
b) in a buffer with pH = 7.3, the total charge on the dipeptide will be close to -2 (the terminal amino group is 100% protonated, both carboxylate groups are 100% deprotonated)
c) in a buffer with pH = 9.6, the total charge on the dipeptide will be close to -2.5 (in this basic buffer, the terminal amino group is 50% deprotonated, and so only contributes a charge of +0.5).
P7.15:
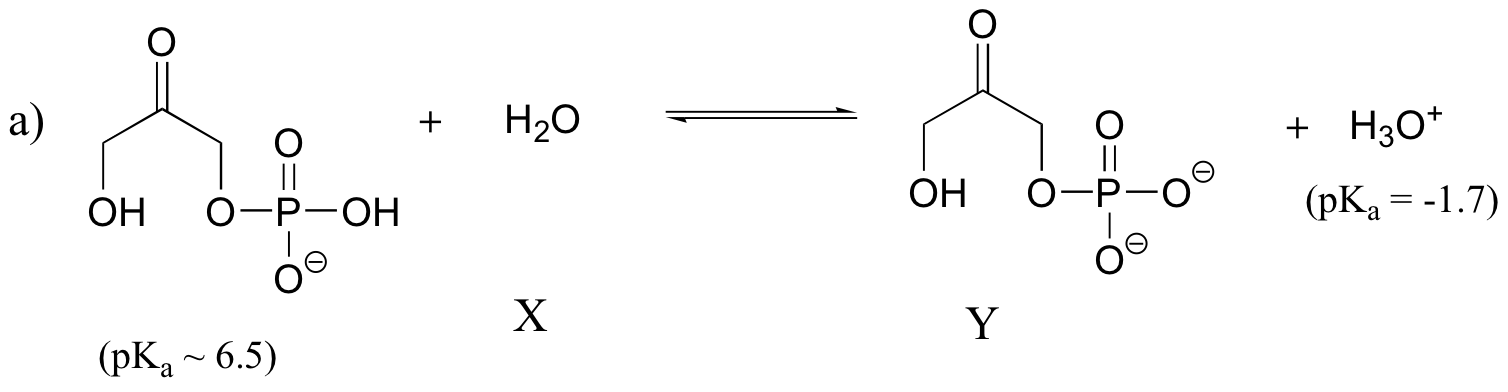
Keq = 10-8.2 = 6.3 x 10-9
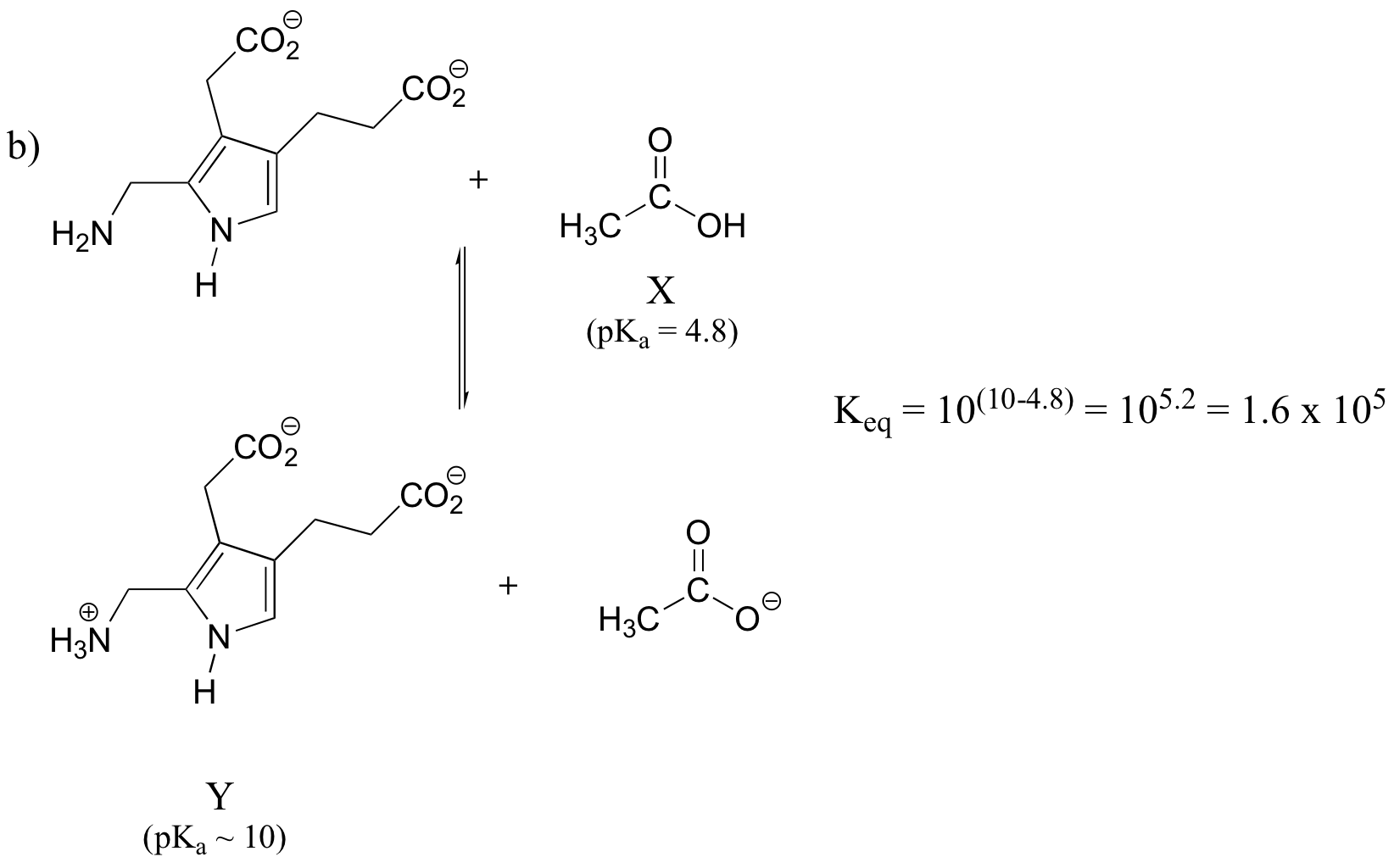
How did we pick the most basic group on the Y species? We have four choices: a primary amine, a 'pyrrole-like' amine, and two carboxylates. We know that pyrrole-like amines are not basic, and we can look at our pKa table to remind ourselves that primary amines are more basic than carboxylates.
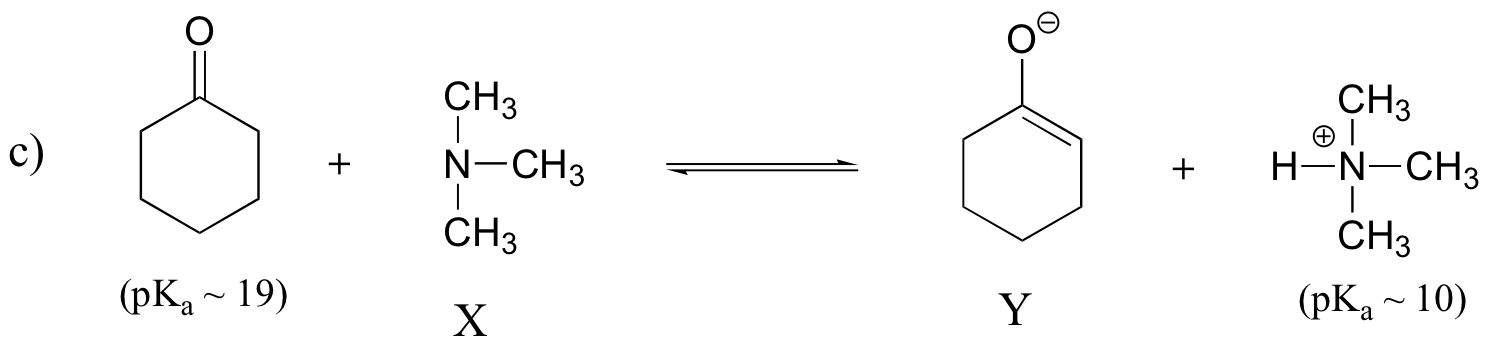
Keq = 10(10-19) = 10-9
P7.16:
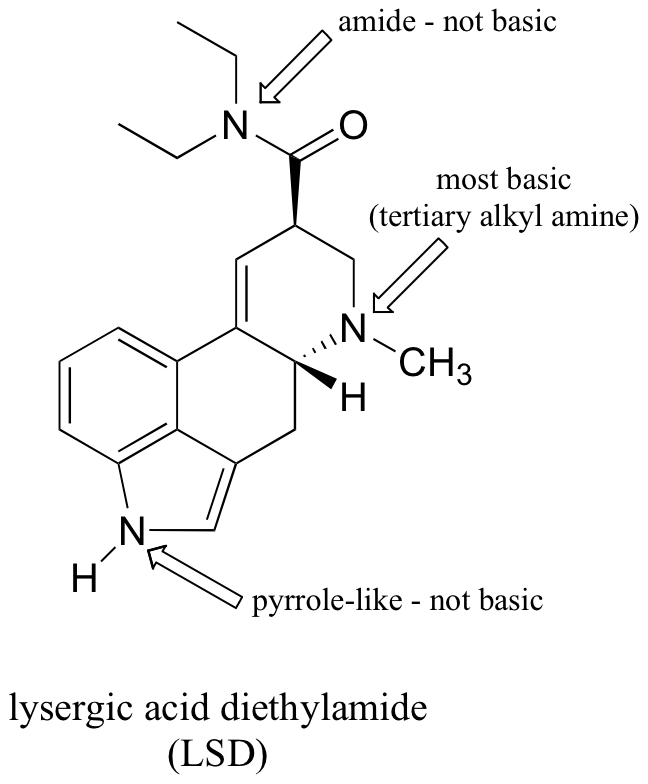
P7.17: Aqueous solutions of 'Tris' and 'HEPES' are very commonly used as buffers in biochemistry and molecular biology laboratories. You make two buffer solutions: One is 50 mM Tris at pH 7.0, the other 50 mM HEPES at pH 7.0. For each solution, calculate the concentration of buffer molecules that are in their charged (ionic) protonation states.
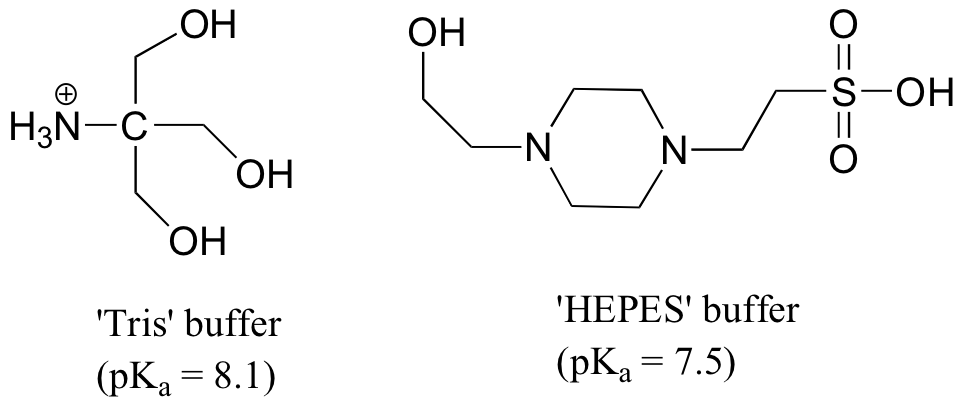
Tris: Using the Henderson-Hasselbalch equation, we find that the ratio [HA+] / [A] at this pH is 10(8.1-7.0) = 101.1 = 12.6. The percentage of HA+ is thus (12.6/13.6)*100 = 93%. The concentration of protonated (positively charged) Tris is (0.93)(50 mM) = 46.5 mM.
HEPES: the most acid proton is on the sulfate group (the negative charge on the conjugate base can be delocalized to two oxygens).
[HA] / [A-] = 100.5 = 3.2. This means 76% is protonated (uncharged) at this pH, and 24% is deprotonated (negatively charged). Thus the concentration of negatively-charged HEPES is (0.24)(50mM) = 12 mM.
Contributors
- Organic Chemistry With a Biological Emphasis, Tim Soderberg (University of Minnesota, Morris)


