7.4: How to Draw Resonance Contributors
- Page ID
- 13866
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Resonance is a mental exercise within the Valence Bond Theory of bonding that describes the delocalization of electrons within molecules. It involves constructing multiple Lewis structures that, when combined, represent the full electronic structure of the molecule. Resonance structures are used when a single Lewis structure cannot fully describe the bonding; the combination of possible resonance structures is defined as a resonance hybrid, which represents the overall delocalization of electrons within the molecule. In general, molecules with multiple resonance structures will be more stable than one with fewer and some resonance structures contribute more to the stability of the molecule than others - formal charges aid in determining this.
Introduction
Resonance is a way of describing delocalized electrons within certain molecules or polyatomic ions where the bonding cannot be expressed by a single Lewis formula. A molecule or ion with such delocalized electrons is represented by several resonance structures. The nuclear skeleton of the Lewis Structure of these resonance structures remains the same, only the electron locations differ. Such is the case for ozone (\(\ce{O3}\)), an allotrope of oxygen with a V-shaped structure and an O–O–O angle of 117.5°. Let's motivate the discussion by building the Lewis structure for ozone.
1. We know that ozone has a V-shaped structure, so one O atom is central:

2. Each O atom has 6 valence electrons, for a total of 18 valence electrons.
3. Assigning one bonding pair of electrons to each oxygen–oxygen bond gives

with 14 electrons left over.
4. If we place three lone pairs of electrons on each terminal oxygen, we obtain

and have 2 electrons left over.
5. At this point, both terminal oxygen atoms have octets of electrons. We therefore place the last 2 electrons on the central atom:

6. The central oxygen has only 6 electrons. We must convert one lone pair on a terminal oxygen atom to a bonding pair of electrons—but which one? Depending on which one we choose, we obtain either
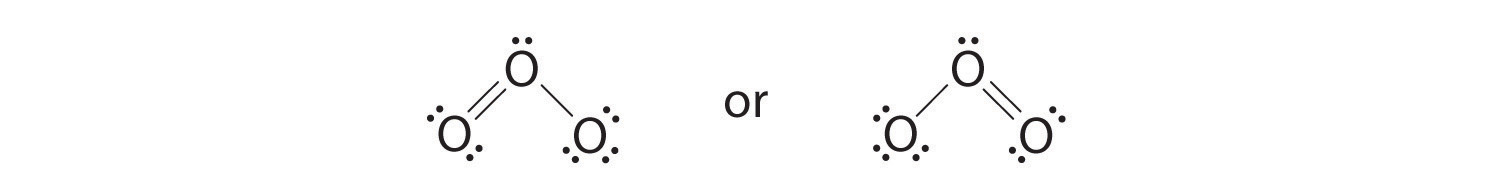
Which is correct? In fact, neither is correct. Both predict one O–O single bond and one O=O double bond. As you will learn, if the bonds were of different types (one single and one double, for example), they would have different lengths. It turns out, however, that both O–O bond distances are identical, 127.2 pm, which is shorter than a typical O–O single bond (148 pm) and longer than the O=O double bond in O2 (120.7 pm).
Equivalent Lewis dot structures, such as those of ozone, are called resonance structures. The position of the atoms is the same in the various resonance structures of a compound, but the position of the electrons is different. Double-headed arrows link the different resonance structures of a compound:

The double-headed arrow indicates that the actual electronic structure is an average of those shown, not that the molecule oscillates between the two structures.
When it is possible to write more than one equivalent resonance structure for a molecule or ion, the actual structure is the average of the resonance structures.
The electrons appear to "shift" between different resonance structures and while not strictly correct as each resonance structure is just a limitation of using the Lewis structure perspective to describe these molecules. A more accurate description of the electron structure of the molecule requires considering multiple resonance structures simultaneously.
- Resonance structures should have the same number of electrons, do not add or subtract any electrons. (check the number of electrons by simply counting them).
- Each resonance structures follows the rules of writing Lewis Structures.
- The hybridization of the structure must stay the same.
- The skeleton of the structure can not be changed (only the electrons move).
- Resonance structures must also have the same number of lone pairs.
Most arrows in chemistry cannot be used interchangeably and care must be given to selecting the correct arrow for the job.
- \(\leftrightarrow\): A double headed arrow on both ends of the arrow between Lewis structures is used to show resonance
- \(\rightleftharpoons\): Double harpoons are used to designate equilibria
- \(\rightharpoonup\): A single harpoon on one end indicates the movement of one electron
- \( \rightarrow \): A double headed arrow on one end is used to indicate the movement of two electrons
Identify the resonance structures for the carbonate ion: \(\ce{CO3^{2-}}\).
Solution
1. Because carbon is the least electronegative element, we place it in the central position:

2. Carbon has 4 valence electrons, each oxygen has 6 valence electrons, and there are 2 more for the −2 charge. This gives 4 + (3 × 6) + 2 = 24 valence electrons.
3. Six electrons are used to form three bonding pairs between the oxygen atoms and the carbon:

4. We divide the remaining 18 electrons equally among the three oxygen atoms by placing three lone pairs on each and indicating the −2 charge:

5. No electrons are left for the central atom.
6. At this point, the carbon atom has only 6 valence electrons, so we must take one lone pair from an oxygen and use it to form a carbon–oxygen double bond. In this case, however, there are three possible choices:
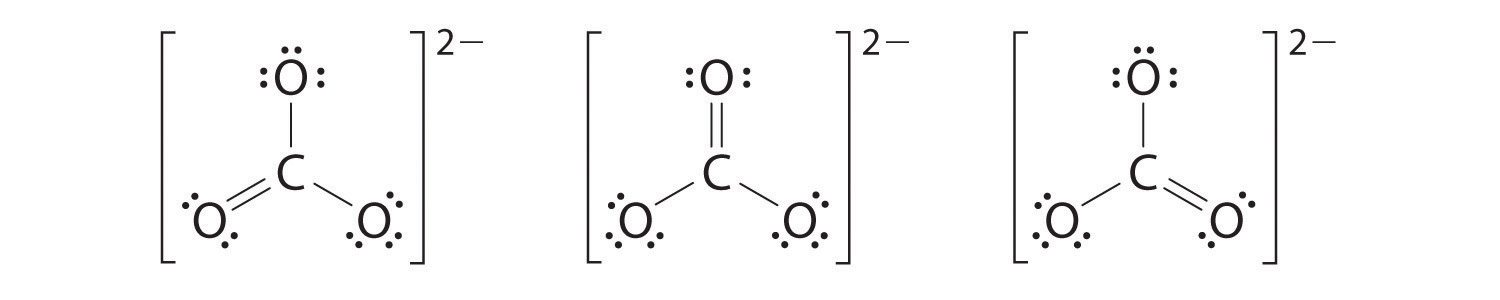
As with ozone, none of these structures describes the bonding exactly. Each predicts one carbon–oxygen double bond and two carbon–oxygen single bonds, but experimentally all C–O bond lengths are identical. We can write resonance structures (in this case, three of them) for the carbonate ion:
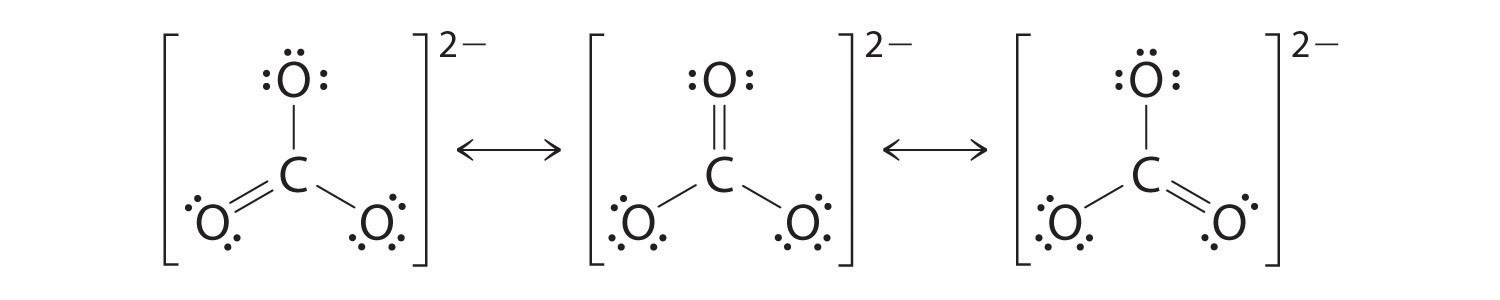
The actual structure is an average of these three resonance structures.
Like ozone, the electronic structure of the carbonate ion cannot be described by a single Lewis electron structure. Unlike O3, though, the actual structure of CO32− is an average of three resonance structures.
Using Formal Charges to Identify viable Resonance Structures
While each resonance structure contributes to the total electronic structure of the molecule, they may not contribute equally. Assigning Formal charges to atoms in the molecules is one mechanism to identify the viability of a resonance structure and determine its relative magnitude among other structures. The formal charge on an atom in a covalent species is the net charge the atom would bear if the electrons in all the bonds to the atom were equally shared. Alternatively the formal charge on an atom in a covalent species is the net charge the atom would bear if all bonds to the atom were nonpolar covalent bonds. To determine the formal charge on a given atom in a covalent species, use the following formula:
\[\text{Formal Charge} = (\text{number of valence electrons in free orbital}) - (\text{number of lone-pair electrons}) - \frac{1}{2} (\text{ number bond pair electrons}) \label{FC}\]
- The greater the number of covalent bonds, the greater the stability since more atoms will have complete octets
- The structure with the least number of formal charges is more stable
- The structure with the least separation of formal charge is more stable
- A structure with a negative charge on the more electronegative atom will be more stable
- Positive charges on the least electronegative atom (most electropositive) is more stable
- Resonance forms that are equivalent have no difference in stability and contribute equally (eg. benzene)
Consider the thiocyanate (\(CNS^-\)) ion.
Solution
1. Find the Lewis Structure of the molecule. (Remember the Lewis Structure rules.)
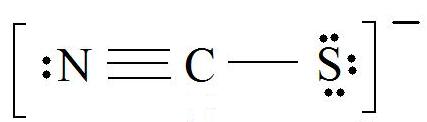
2. Resonance: All elements want an octet, and we can do that in multiple ways by moving the terminal atom's electrons around (bonds too).
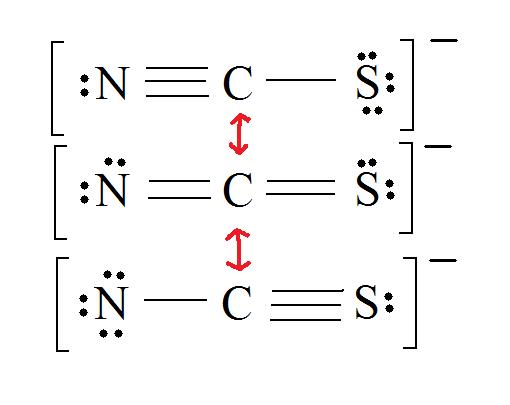
3. Assign Formal Charges via Equation \ref{FC}.
Formal Charge = (number of valence electrons in free orbital) - (number of lone-pair electrons) - ( \( \frac{1}{2} \) number bond pair electrons)
Remember to determine the number of valence electron each atom has before assigning Formal Charges
C = 4 valence e-, N = 5 valence e-, S = 6 valence e-, also add an extra electron for the (-1) charge. The total of valence electrons is 16.

4. Find the most ideal resonance structure. (Note: It is the one with the least formal charges that adds up to zero or to the molecule's overall charge.)


5. Now we have to look at electronegativity for the "Correct" Lewis structure.
The most electronegative atom usually has the negative formal charge, while the least electronegative atom usually has the positive formal charges.

It is useful to combine the resonance structures into a single structure called the Resonance Hybrid that describes the bonding of the molecule. The general approach is described below:
- Draw the Lewis Structure & Resonance for the molecule (using solid lines for bonds).
- Where there can be a double or triple bond, draw a dotted line (-----) for the bond.
- Draw only the lone pairs found in all resonance structures, do not include the lone pairs that are not on all of the resonance structures.
Benzene is a common organic solvent that was previously used in gasoline; it is no longer used for this purpose, however, because it is now known to be a carcinogen. The benzene molecule (\(\ce{C6H6}\)) consists of a regular hexagon of carbon atoms, each of which is also bonded to a hydrogen atom. Use resonance structures to describe the bonding in benzene.
Given: molecular formula and molecular geometry
Asked for: resonance structures
Strategy:
- Draw a structure for benzene illustrating the bonded atoms. Then calculate the number of valence electrons used in this drawing.
- Subtract this number from the total number of valence electrons in benzene and then locate the remaining electrons such that each atom in the structure reaches an octet.
- Draw the resonance structures for benzene.
Solution:
A Each hydrogen atom contributes 1 valence electron, and each carbon atom contributes 4 valence electrons, for a total of (6 × 1) + (6 × 4) = 30 valence electrons. If we place a single bonding electron pair between each pair of carbon atoms and between each carbon and a hydrogen atom, we obtain the following:
Each carbon atom in this structure has only 6 electrons and has a formal charge of +1, but we have used only 24 of the 30 valence electrons.
B If the 6 remaining electrons are uniformly distributed pairwise on alternate carbon atoms, we obtain the following:
Three carbon atoms now have an octet configuration and a formal charge of −1, while three carbon atoms have only 6 electrons and a formal charge of +1. We can convert each lone pair to a bonding electron pair, which gives each atom an octet of electrons and a formal charge of 0, by making three C=C double bonds.
C There are, however, two ways to do this:
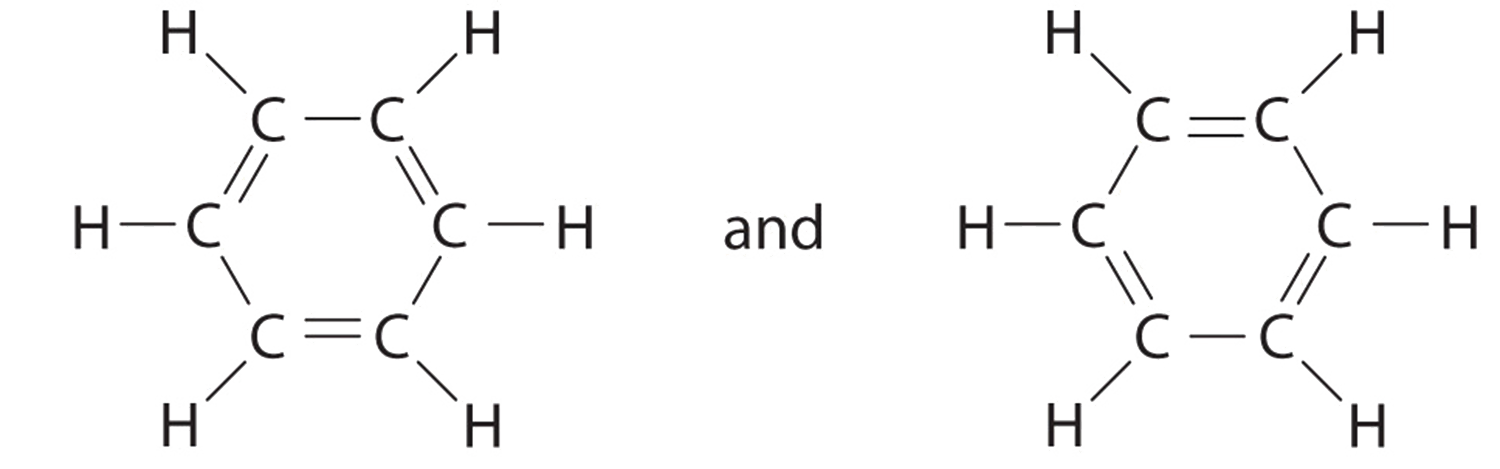
Each structure has alternating double and single bonds, but experimentation shows that each carbon–carbon bond in benzene is identical, with bond lengths (139.9 pm) intermediate between those typically found for a C–C single bond (154 pm) and a C=C double bond (134 pm). We can describe the bonding in benzene using the two resonance structures, but the actual electronic structure is an average of the two. The existence of multiple resonance structures for aromatic hydrocarbons like benzene is often indicated by drawing either a circle or dashed lines inside the hexagon:
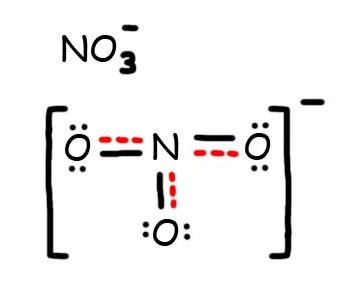
Draw the possible resonance structures for the Nitrate ion \(\ce{NO_3^{-}}\).
Solution
1. Count up the valence electrons: (1*5) + (3*6) + 1(ion) = 24 electrons
2. Draw the bond connectivities:
3. Add octet electrons to the atoms bonded to the center atom:
4. Place any leftover electrons (24-24 = 0) on the center atom:
5. Does the central atom have an octet?
- NO, it has 6 electrons
- Add a multiple bond (first try a double bond) to see if the central atom can achieve an octet:
6. Does the central atom have an octet?
- YES
- Are there possible resonance structures? YES
Note: We would expect that the bond lengths in the \(\ce{NO_3^{-}}\) ion to be somewhat shorter than a single bond.
References
- Petrucci, Ralph H., et al. General Chemistry: Principles and Modern Applications. New Jersey: Pearson Prentice Hall, 2007.
- Ahmad, Wan-Yaacob and Zakaria, Mat B. "Drawing Lewis Structures from Lewis Symbols: A Direct Electron Pairing Approach." Journal of Chemical Education: Journal 77.3.
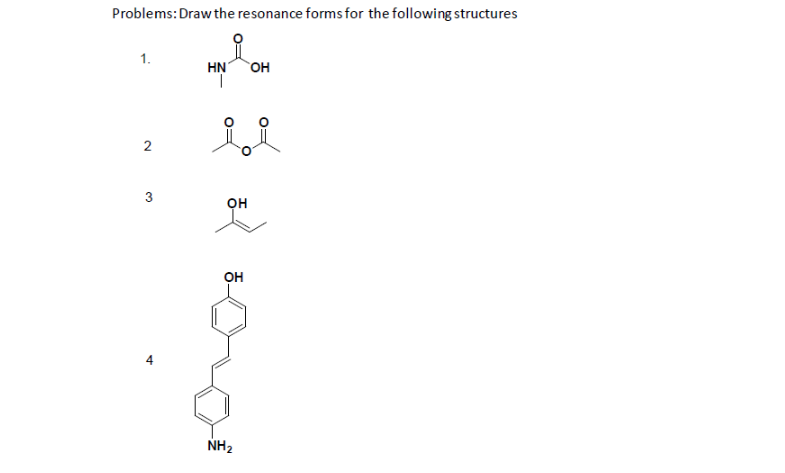
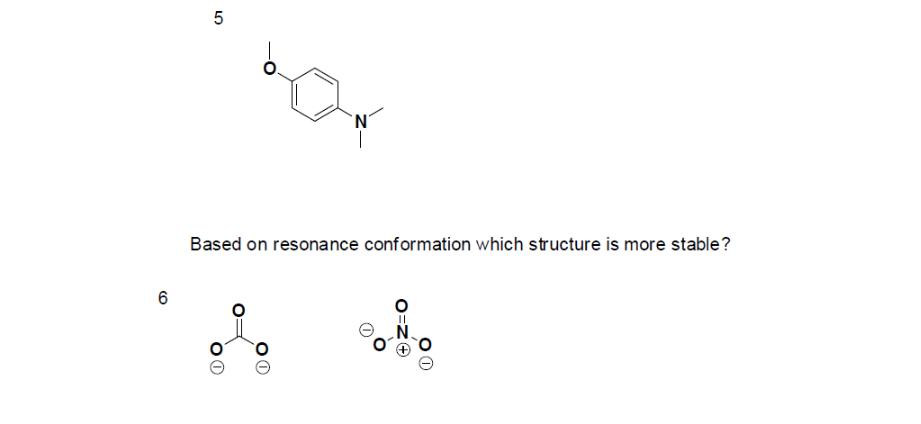
Problems
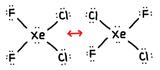
- True or False, The picture below is a resonance structure?
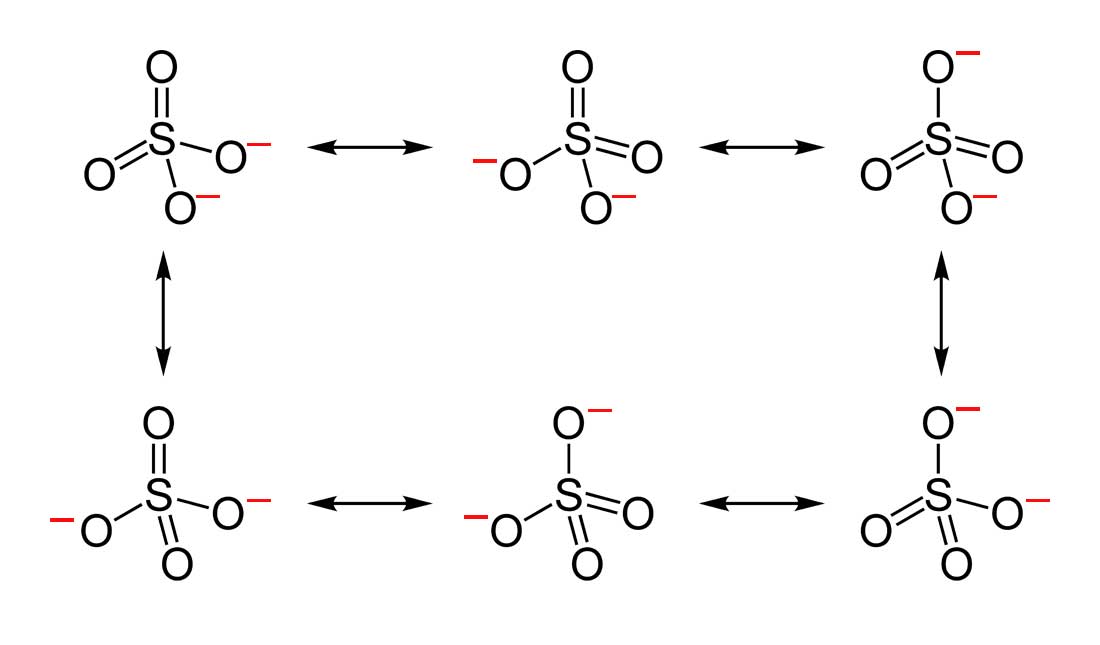
- Draw the Lewis Dot Structure for SO42- and all possible resonance structures. Which of the following resonance structure is not favored among the Lewis Structures? Explain why. Assign Formal Charges.
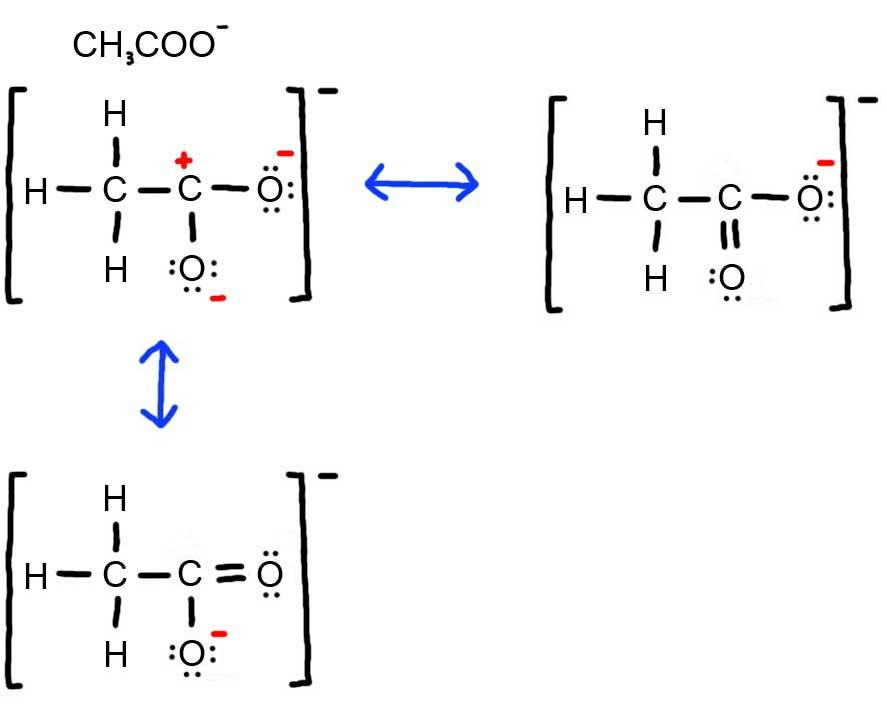
- Draw the Lewis Dot Structure for CH3COO- and all possible resonance structures. Assign Formal Charges. Choose the most favorable Lewis Structure.
- Draw the Lewis Dot Structure for HPO32- and all possible resonance structures. Assign Formal Charges.
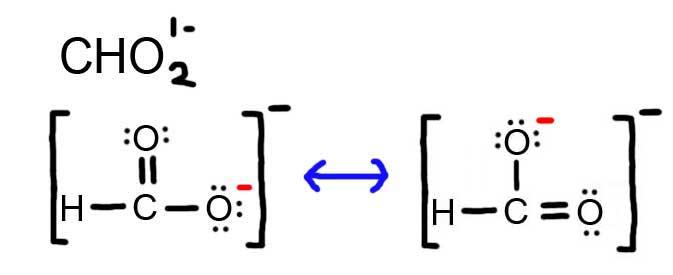
- Draw the Lewis Dot Structure for CHO21- and all possible resonance structures. Assign Formal Charges.
- Draw the Resonance Hybrid Structure for PO43-.
- Draw the Resonance Hybrid Structure for NO3-.
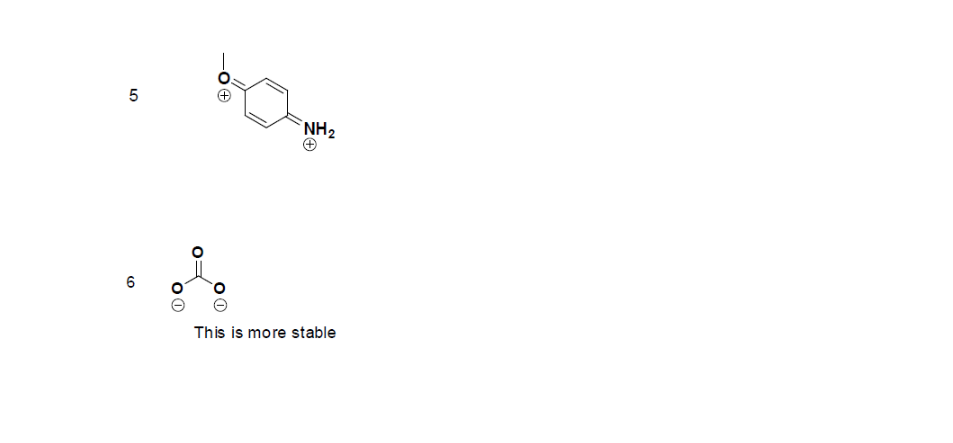
Answers
1. False, because the electrons were not moved around, only the atoms (this violates the Resonance Structure Rules).
2. Below are the all Lewis dot structure with formal charges (in red) for Sulfate (SO42-). There isn't a most favorable resonance of the Sulfate ion because they are all identical in charge and there is no change in Electronegativity between the Oxygen atoms.
3. Below is the resonance for CH3COO-, formal charges are displayed in red. The Lewis Structure with the most formal charges is not desirable, because we want the Lewis Structure with the least formal charge.
4. The resonance for HPO32-, and the formal charges (in red).
5. The resonance for CHO21-, and the formal charges (in red).
6. The resonance hybrid for PO43-, hybrid bonds are in red.

7. The resonance hybrid for NO3-, hybrid bonds are in red.
Contributors and Attributions
- Sharon Wei (UCD), Liza Chu (UCD)