1.14: Summary: Hybridization, Bond Lengths, Bond Strengths, and Bond Angles
- Page ID
- 17867
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Bond order is the number of chemical bonds between a pair of atoms and indicates the stability of a bond. For example, in diatomic nitrogen, N≡N, the bond order is 3; in acetylene, H−C≡C−H, the carbon-carbon bond order is also 3, and the C−H bond order is 1. Bond order and bond length indicate the type and strength of covalent bonds between atoms. Bond order and length are inversely proportional to each other: when bond order is increased, bond length is decreased.
Introduction
Chemistry deals with the way in which subatomic particles bond together to form atoms. Chemistry also focuses on the way in which atoms bond together to form molecules. In the atomic structure, electrons surround the atomic nucleus in regions called orbitals. Each orbital shell can hold a certain number of electrons. When the nearest orbital shell is full, new electrons start to gather in the next orbital shell out from the nucleus, and continue until that shell is also full. The collection of electrons continues in ever widening orbital shells as larger atoms have more electrons than smaller atoms. When two atoms bond to form a molecule, their electrons bond them together by mixing into openings in each others' orbital shells. As with the collection of electrons by the atom, the formation of bonds by the molecule starts at the nearest available orbital shell opening and expand outward.
Bond Order
Bond order is the number of bonding pairs of electrons between two atoms. In a covalent bond between two atoms, a single bond has a bond order of one, a double bond has a bond order of two, a triple bond has a bond order of three, and so on. To determine the bond order between two covalently bonded atoms, follow these steps:
- Draw the Lewis structure.
- Determine the type of bonds between the two atoms.
- 0: No bond
- 1: Single bond
- 2: double bond
- 3: triple bond
If the bond order is zero, the molecule cannot form. The higher bond orders indicate greater stability for the new molecule. In molecules that have resonance bonding, the bond order does not need to be an integer.
Determine the bond order for cyanide, CN-.
Solution
1) Draw the Lewis structure.
2) Determine the type of bond between the two atoms.
Because there are 3 dashes, the bond is a triple bond. A triple bond corresponds to a bond order of 3.
Determine the bond order for hydrogen gas, H2.
Solution
1) Draw the Lewis structure.
![]()
2) Determine the type of bond between the two atoms.
There is only one pair of shared electrons (or dash), indicating is a single bond, with a bond order of 1.
Polyatomic molecules
If there are more than two atoms in the molecule, follow these steps to determine the bond order:
- Draw the Lewis structure.
- Count the total number of bonds.
- Count the number of bond groups between individual atoms.
- Divide the number of bonds between atoms by the total number of bond groups in the molecule.
Determine the bond order for nitrate, \(NO_3^-\).
Solution
1) Draw the Lewis structure.
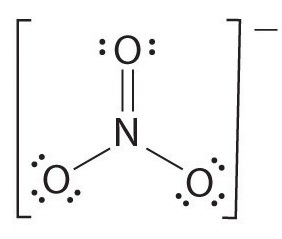
2) Count the total number of bonds.
4
The total number of bonds is 4.
3) Count the number of bond groups between individual atoms.
3
The number of bond groups between individual atoms is 3.
4) Divide the number of bonds between individual atoms by the total number of bonds.
\[\dfrac{4}{3}= 1.33 \]
The bond order is 1.33
Determine the bond order for nitronium ion: \(NO_2^+\).
Solution
1) Draw the Lewis Structure.
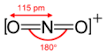
2) Count the total number of bonds.
4
The total number of bonds is 4.
3) Count the number of bond groups between individual atoms.
2
The number of bond groups between atoms is 2.
4) Divide the bond groups between individual atoms by the total number of bonds.
\[\frac{4}{2} = 2\]
The bond order is 2.
A high bond order indicates more attraction between electrons. A higher bond order also means that the atoms are held together more tightly. With a lower bond order, there is less attraction between electrons and this causes the atoms to be held together more loosely. Bond order also indicates the stability of the bond. The higher the bond order, the more electrons holding the atoms together, and therefore the greater the stability.
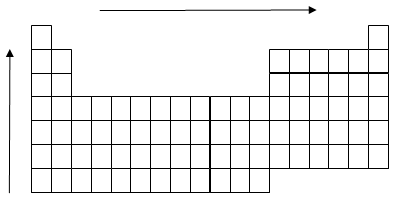
Trends in the Periodic Table
Bond order increases across a period and decreases down a group.
Bond Length
Bond length is defined as the distance between the centers of two covalently bonded atoms. The length of the bond is determined by the number of bonded electrons (the bond order). The higher the bond order, the stronger the pull between the two atoms and the shorter the bond length. Generally, the length of the bond between two atoms is approximately the sum of the covalent radii of the two atoms. Bond length is reported in picometers. Therefore, bond length increases in the following order: triple bond < double bond < single bond.
To find the bond length, follow these steps:
- Draw the Lewis structure.
- Look up the chart below for the radii for the corresponding bond.
- Find the sum of the two radii.
Determine the carbon-to-chlorine bond length in CCl4.
Solution
Using Table A3, a C single bond has a length of 75 picometers and that a Cl single bond has a length of 99 picometers. When added together, the bond length of a C-Cl bond is approximately 174 picometers.
Determine the carbon-oxygen bond length in CO2.
Solution
Using Table A3, we see that a C double bond has a length of 67 picometers and that an O double bond has a length of 57 picometers. When added together, the bond length of a C=O bond is approximately 124 picometers.
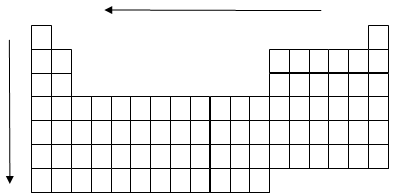
Trends in the Periodic Table
Because the bond length is proportional to the atomic radius, the bond length trends in the periodic table follow the same trends as atomic radii: bond length decreases across a period and increases down a group.
Problems
- What is the bond order of \(O_2\)?
- What is the bond order of \(NO_3^-\)?
- What is the carbon-nitrogen bond length in \(HCN\)?
- Is the carbon-to-oxygen bond length greater in \(CO_2\) or \(CO\)?
- What is the nitrogen-fluoride bond length in \(NF_3\)?
Solutions
1. First, write the Lewis structure for \(O_2\).
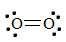
There is a double bond between the two oxygen atoms; therefore, the bond order of the molecule is 2.
2. The Lewis structure for NO3- is given below:
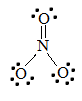
To find the bond order of this molecule, take the average of the bond orders. N=O has a bond order of two, and both N-O bonds have a bond order of one. Adding these together and dividing by the number of bonds (3) reveals that the bond order of nitrate is 1.33.
3. To find the carbon-nitrogen bond length in HCN, draw the Lewis structure of HCN.
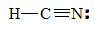
The bond between carbon and nitrogen is a triple bond, and a triple bond between carbon and nitrogen has a bond length of approximately 60 + 54 =114 pm.
4. From the Lewis structures for CO2 and CO, there is a double bond between the carbon and oxygen in CO2 and a triple bond between the carbon and oxygen in CO.

Referring to the table above, a double bond between carbon and oxygen has a bond length of approximately 67 + 57 = 124 pm and a triple bond between carbon and oxygen has a bond length of approximately 60 + 53 =113 pm. Therefore, the bond length is greater in CO2.
Another method makes use of the fact that the more electron bonds between the atoms, the tighter the electrons are pulling the atoms together. Therefore, the bond length is greater in CO2.
5. To find the nitrogen-to-fluorine bond length in NF3, draw the Lewis structure.
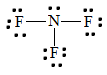
The bond between fluorine and nitrogen is a single bond. From the table above, a single bond between fluorine and nitrogen has a bond length of approximately 64 + 71 =135 pm.
References
- Campbell, Neil A., Brad Williamson, and Robin J. Heyden. Biology: Exploring Life. Boston, Massachusetts: Pearson Prentice Hall, 2006.
- Petrucci, Ralph H., Harwood, William S., Herring, F. G., and Madura Jeffrey D. General Chemistry: Principles & Modern Applications. 9th Ed. New Jersey: Pearson Education, Inc., 2007. Print.
- Cordero, Beatriz, Verónica Gómez, Ana E. Platero-Prats, Marc Revés, Jorge Echeverría, Eduard Cremades, Flavia Barragán and Santiago Alvarez. Dalton's Transactions." Covalent radii revisited 2008:
- Pekka Pyykkö and Michiko Atsumi, Chem. Eur. J. Molecular Double-Bond Covalent Radii for Elements Li–E112 2009
Contributors and Attributions
- Wikihow.com
- Anonymous

