5.7: Spin-Spin Splitting in Proton NMR Spectra

Objectives

After completing this section, you should be able to

1. understand what spin-spin splitting is and what information it tells you
2. explain the spin-spin splitting pattern observed in the ¹H NMR spectrum of a simple organic compound.
3. interpret the splitting pattern of a given ¹H NMR spectrum.
4. determine the structure of a relatively simple organic compound, given its ¹H NMR spectrum and other relevant information.
5. use coupling constants to determine which groups of protons are coupling with one another in a ¹H NMR spectrum.
6. predict the splitting pattern which should be observed in the ¹H NMR spectrum of a given organic compound.

Key Terms

Make certain that you can define, and use in context, the key terms below.

• coupling constant
• multiplet
• quartet
• triplet
• doublet

From what we have learned about ¹H NMR spectra so far, we might predict that the spectrum of 1-chloroethane, CH₃CH₂Cl, would consist of two peaks—one, at about 0.9 δ, expected for CH₃ and one shifted downfield because of the presence of an additional electronegative chlorine atom on the second carbon. However, when we look at the spectrum (below) it appears to be much more complex. True, we see absorptions in the regions we predicted, but instead of the single peak we have seen thus far, these absorptions appear as a group of three peaks (a triplet) and a group of four peaks (a quartet). This complication is in fact very useful to the organic chemist, and adds greatly to the power of NMR spectroscopy as a tool for the elucidation of chemical structures. The split peaks (multiplets) arise because the magnetic field experienced by the protons of one group is influenced by the spin arrangements of the protons in an adjacent group.

The source of spin-spin coupling

The ¹H-NMR spectra that we have seen so far (of methyl acetate and para-xylene) are somewhat unusual in the sense that in both of these molecules, each set of protons generates a single NMR signal. In fact, the ¹H-NMR spectra of most organic molecules contain proton signals that are split into two or more sub-peaks. This splitting behavior actually provides us with more information about our sample molecule.

Consider the spectrum for 1,1,2-trichloroethane. In this and in many spectra to follow, enlargements of individual signals will be shown so that the signal splitting patterns are recognizable.

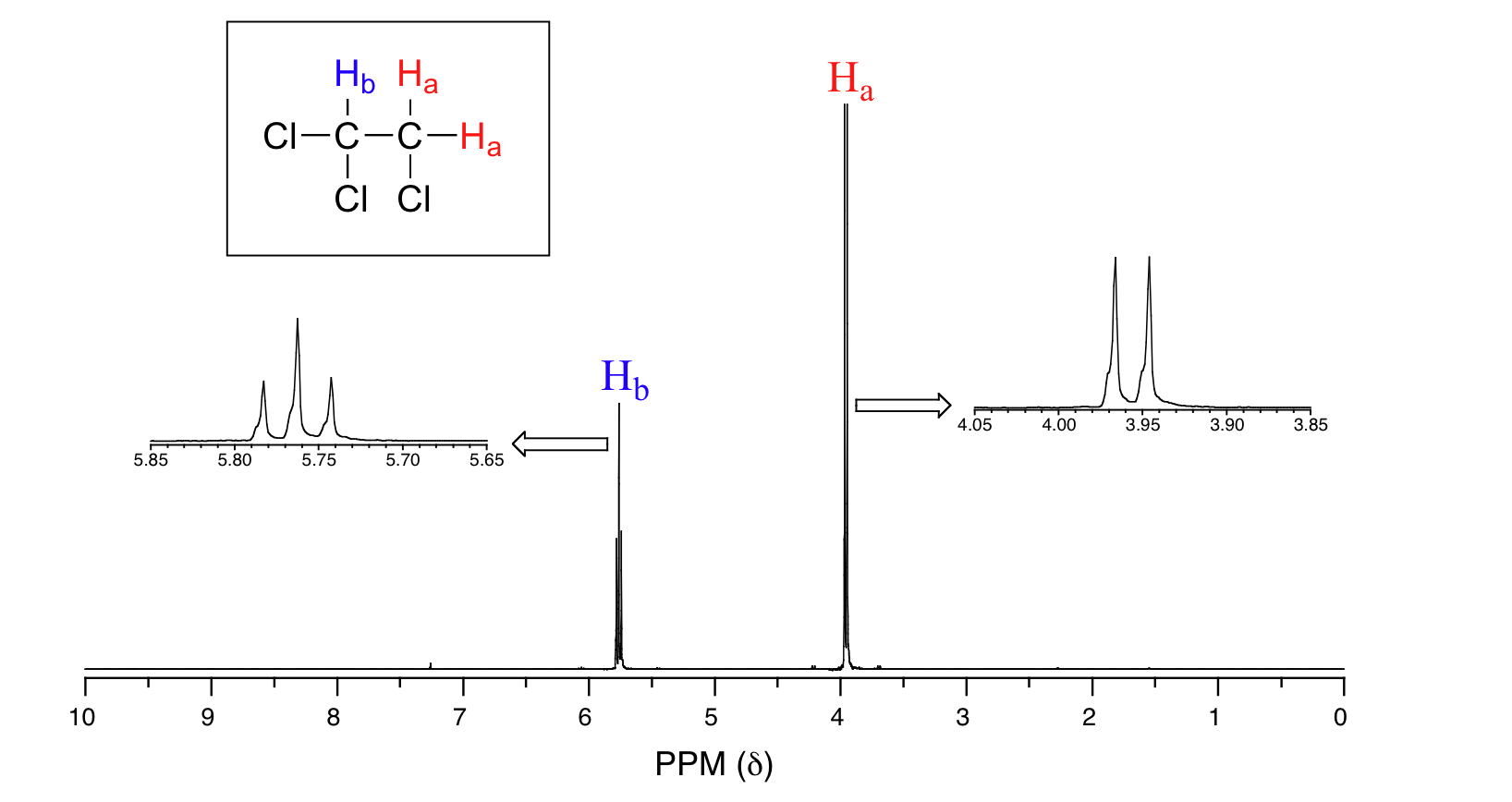
The signal at 3.96 ppm, corresponding to the two H_a protons, is split into two subpeaks of equal height (and area) – this is referred to as a doublet. The two H_b protons at 5.76 ppm, on the other hand, is split into three sub-peaks, with the middle peak higher than the two outside peaks - if we were to integrate each subpeak, we would see that the area under the middle peak is twice that of each of the outside peaks. This is called a triplet.

The source of signal splitting is a phenomenon called spin-spin coupling, a term that describes the magnetic interactions between neighboring, non-equivalent NMR-active nuclei. In our 1,1,2--trichloroethane example, the H_a and H_b protons are spin-coupled to each other. Here's how it works, looking first at the H_b signal. The magnetic environment experienced by H_b is influenced by the fields of both neighboring H_a protons, which we will call H_a1 and H_a2. There are four possibilities here, each of which is equally probable. First, the magnetic fields of both H_a1 and H_a2 could be aligned with B₀, which would deshield H_b, shifting its NMR signal slightly downfield. Second, both the H_a1 and H_a2 magnetic fields could be aligned opposed to B₀, which would shield H_b, shifting its resonance signal slightly upfield due to being more shielded. Third and fourth, H_a1 could be with B₀ and H_a2 opposed, or H_a1 opposed to B₀ and H_a2 with B₀. In each of the last two cases, the shielding effect of one H_a proton would cancel the deshielding effect of the other, and the chemical shift of H_b would be unchanged. These ideas an be illustrated by a splitting diagram, as shown below.

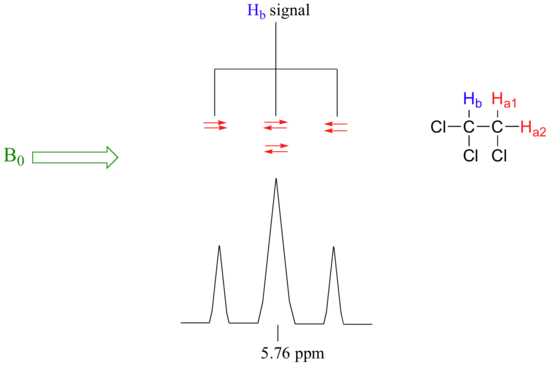
So in the end, the signal for H_b is a triplet, with the middle peak twice as large as the two outer peaks because there are two ways that H_a1 and H_a2 can cancel each other out.

The H_a hydrogens give rise to a doublet signal at 3.96 ppm – notice that the two peaks are equal in height to one another. This splitting pattern results from the spin-coupling effect of the one H_b hydrogen next door, and can be explained by an analysis similar to that which we used to explain the triplet pattern above. The proton could be aligned with the magnetic field, which would deshield H_a or it could oppose the magnetic field, which would shield H_a.

Example \(\PageIndex{1}\)

Now, consider the spectrum for ethyl acetate:

Explain the splitting patterns of H_a, H_b, and H_c in ethyl acetate.

Solution

We see an unsplit singlet peak at 1.83 ppm that corresponds to the acetyl (H_a) hydrogens. This signal is unsplit because there are no hydrogens on the adjacent carbon. The signal at 1.055 ppm for the H_c hydrogens is split into a triplet by the two H_b hydrogens next door. The explanation here is the same as the explanation for the triplet peak we saw previously for 1,1,2-trichloroethane.

The H_b hydrogens give rise to a quartet signal at 3.91 ppm – notice that the two middle peaks are taller then the two outside peaks. This splitting pattern results from the spin-coupling effect of the three H_c hydrogens next door, and can be explained by an analysis similar to that which we used to explain the doublet and triplet patterns previously discussed.

Instead of drawing a splitting diagram for every molecule, there is a recognizable pattern which is usually referred to as the n + 1 rule: if a set of hydrogens has n neighboring, non-equivalent hydrogens, it will be split into n + 1 subpeaks. This is very useful information if we are trying to determine the structure of an unknown molecule: if we see a triplet signal, we know that the corresponding hydrogen or set of hydrogens has two neighboring hydrogens. When we begin to determine structures of unknown compounds using ¹H-NMR spectral data, it will become more apparent how this kind of information can be used.

Three important points need to be emphasized here. First, signal splitting only occurs between non-equivalent hydrogens – in other words, H_a1 in 1,1,2-trichloroethane is not split by H_a2, and vice-versa.

Second, splitting occurs primarily between hydrogens that are separated by three bonds. This is why the H_a hydrogens in ethyl acetate form a singlet– the nearest hydrogen neighbors are five bonds away (count the bonds between hydrogen to hydrogen), too far for coupling to occur.

Occasionally we will see four-bond and even 5-bond splitting, but in these cases the magnetic influence of one set of hydrogens on the other set is much more subtle than what we typically see in three-bond splitting (more complex coupling interactions is provided in section 5.8).

Finally, splitting is most noticeable with hydrogens bonded to carbon. Hydrogens that are bonded to heteroatoms (alcohol or amino hydrogens, for example) are coupled weakly - or not at all - to their neighbors. This has to do with the fact that these protons exchange rapidly with solvent or other sample molecules, which is greatly enhanced by even traces of acid or base (see mechanism with ethanol below). Remember, NMR is like a camera that takes photographs of a rapidly moving object with a slow shutter speed - the result is a blurred image. This blurred image here creates a broader singlet for exchanging protons, even if there are neighboring hydrogens. 

To see the splitting of exchangeable protons, the NMR experiment needs to be carried out as low temperatures. 

Multiplicity in Proton NMR

The number of lines in a peak is always one more (n+1) than the number of hydrogens on the neighboring carbon. This table summarizes coupling patterns that arise when protons have different numbers of neighbors.

# of lines	ratio of lines	term for peak	# of neighbors
1	-	singlet	0
2	1:1	doublet	1
3	1:2:1	triplet	2
4	1:3:3:1	quartet	3
5	1:4:6:4:1	quintet	4
6	1:5:10:10:5:1	sextet	5
7	1:6:15:20:15:6:1	septet	6
8	1:7:21:35:35:21:7:1	octet	7
9	1:8:28:56:70:56:28:8:1	nonet	8

Coupling constants

Chemists quantify the spin-spin coupling effect using something called the coupling constant, which is abbreviated with the capital letter J. The coupling constant is simply the difference, expressed in Hz (not ppm), between two adjacent sub-peaks in a split signal. For our triplet in the 1,1,2-trichloroethane spectrum, for example, the three subpeaks are separated by 6.1 Hz, and thus we write ³J_a-b = 6.1 Hz.

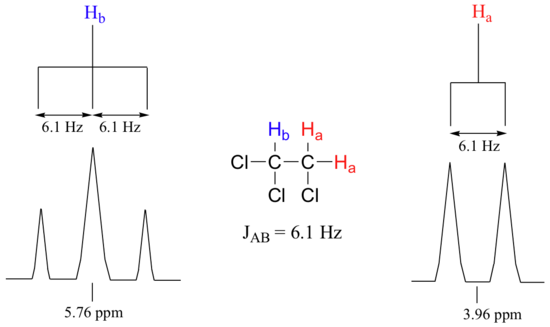
The superscript 3 tells us that this is a three-bond coupling interaction, and the a-b subscript tells us that we are talking about coupling between H_a and H_b. Unlike the chemical shift value, the coupling constant, expressed in Hz, is the same regardless of the applied field strength of the NMR magnet. This is because the strength of the magnetic moment of a neighboring proton, which is the source of the spin-spin coupling phenomenon, does not depend on the applied field strength. Also, the coupling constant ³J_a-b quantifies the magnetic interaction between the H_a and H_b hydrogen sets, and this interaction is of the same magnitude in either direction. In other words, H_a influences H_b to the same extent that H_b influences H_a. When looking at more complex NMR spectra (Section 5.8), this idea of reciprocal coupling constants can be very helpful in identifying the coupling relationships between proton sets.

Similar types of bonds lead to similar coupling constants and this has resulted in a range for particular types of hydrogens interacting through a particular bond. For example, coupling constants between proton sets on neighboring sp³-hybridized carbons (3 bonds) is typically in the region of 6-8 Hz. The table below lists typical three-bond coupling constant values for different types of bonds. Remember, chemically equivalent protons do not couple with one another to give spin-spin splitting.

Type of bond	Image of type of bond	Coupling constant (Hz)
Standard three bond coupling		6-8
Vinylic geminal coupling		0-3
Vinylic cis coupling		6-15
Vinylic trans coupling		11-18
Benzylic ortho coupling		6-10
Benzylic meta coupling*		0-4
Aldehydic proton coupling		2-3

*Actually 4-bond coupling.

Exercise

Exercise \(\PageIndex{1}\)

Predict the splitting patterns of the following molecules:

a) 

b) 

Answer

a) There are three types of protons, so there will be three peaks. The methyl directly attached to the oxygen will be a singlet. The methylene will be split into a quartet by the neighboring methyl group. The other methyl group will be split into a triplet by the neighboring -CH₂-.

b) This molecule is symmetrical, which leads to two types of hydrogens and therefore two peaks. The methylene will be split into a triplet by the two neighboring hydrogens on either side. The -CH- peak will be split into a triplet as well due to the neighboring -CH₂-.

Exercise \(\PageIndex{2}\)

How many proton signals would you expect to see in the ¹H-NMR spectrum of the structure shown below? For each of the proton signals, predict the splitting pattern. Assume that you see only 3-bond coupling.

Answer

Because of the symmetry in the molecule, there are only four proton signals.

OH proton = singlet

H_a = singlet

H_b = doublet

H_c = doublet

 

Exercise \(\PageIndex{3}\)

The following spectrum is for C₄H₁₀O. Determine the structure. The ratio of integrals from left to right is 2:3.

Answer

The total number of hydrogens is 2+3 = 5. All the hydrogens are not accounted for since we need a total of 10 hydrogens. This means there is symmetry in the molecule. Ten is divisible by five. If we multiply each in the 2:3 ratio, then we get 4:6, which does add to 10.

Typically, integrations of 3 or multiples of 3 are methyl groups. The peak at 1.14 ppm is a methyl group with two neighbors, since the peak is split into a triplet. n +1 = 3, n = 2, n = number of neighbors. The first fragment is a -CH₂-CH₃. There are two of these fragments, since there are actually 6 total methyl protons. 

The peak at 3.43 ppm integrates to 4 and is a quartet. The integration indicates it is a methylene group and since it is a quartet, it must have three neighbors. So far, the fragment would be -CH₂-CH₃. It is also very far downfield for a proton just bonded to other carbons with hydrogens, which would typically be around 1.2-1.7 ppm (see the table in Section 5.5). This means it must be attached to an electron withdrawing group. The electron withdrawing group in this molecule is the -O-. Our final fragment is CH₃-CH₂-O-. 

If we look at all of our fragments, we can begin to put them together. Let's take the two fragments (-CH₂-CH₃ and -O-CH₂-CH₃), each makes one more bond. If you connect them, then you would get CH₃-CH₂-O-CH₂-CH₃. The molecule is symmetrical with two types of protons with teh 4:6 (or 2:3) ratio and correct splitting pattern. This spectrum correlates to diethyl ether.

Contributors and Attributions

• Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)

• Prof. Steven Farmer (Sonoma State University)

• Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

• Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)