8.4: Electrophiles
- Page ID
- 106339
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Next, we turn to electrophiles. In the vast majority of the nucleophilic substitution reactions you will see in this and other organic chemistry texts, the electrophilic atom is a carbon bonded to an electronegative atom, usually oxygen, nitrogen, sulfur, or a halogen. The concept of electrophilicity is relatively simple: an electron-poor atom is an attractive target for something that is electron-rich, i.e. a nucleophile. However, we must also consider the effect of steric hindrance on electrophilicity.
Steric hindrance at the electrophile
One of the most important factors to consider when looking at the electrophile in a nucleophilic substitution reaction is steric hindrance. Consider two hypothetical \(S_N2\) reactions: one in which the electrophile is a methyl carbon and another in which it is tertiary carbon.
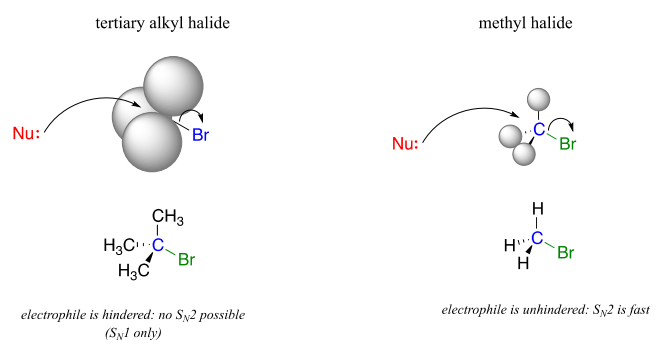
Because the three substituents on the methyl electrophile are hydrogen atoms, the nucleophile has a relatively clear path for backside attack, and the \(S_N2\) reaction will take place readily. However, backside attack on the tertiary carbon electrophile is blocked by the bulky methyl groups, preventing access to the site of electrophilicity.
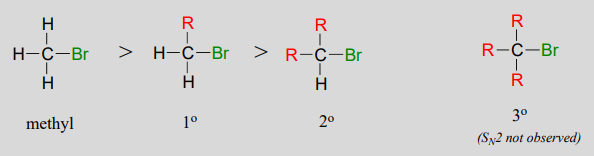
\(S_N2\) reactions occur at methyl, primary, and secondary carbon electrophiles. The degree of steric hindrance determines relative rates of reaction: unhindered methyl electrophiles react fastest, and more hindered secondary carbon electrophiles react slowest, assuming all other reactions conditions are identical. \(S_N2\) reactions do not occur to an appreciable extent at tertiary carbon electrophiles.
Which would be expected to react more rapidly in an \(S_N2\) reaction with an azide ion (\(N_3^-\)) nucleophile in acetone solvent: 1-bromo-2,2-dimethylbutane or 1-bromo-3-methylbutane?
What about the \(S_N1\) pathway? Steric hindrance around the electrophilic carbon is not a significant factor in slowing down an \(S_N1\) reaction. This makes perfect sense from a geometric point of view: the limitations imposed by sterics are significant in an \(S_N2\) displacement because the electrophile being attacked is an sp3-hybridized tetrahedral carbon with relatively ‘tight’ angles of \(109.5^{\circ}\). Remember that in an \(S_N1\) mechanism, the leaving group leaves first, and then the nucleophile attacks an \(sp^2\)-hybridized carbocation intermediate, which has trigonal planar geometry with ‘open’ \(120^{\circ}\) angles.
artwork needed
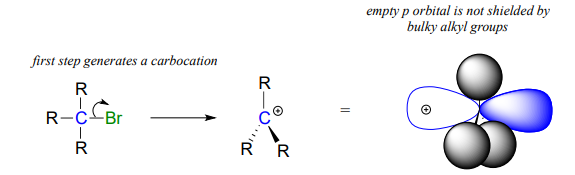
With this open geometry, the empty p orbital of the carbocation is no longer significantly shielded from the approaching nucleophile by the bulky alkyl groups, and is an 'easy target' for a nucleophile: this step is fast, and is not the rate-determining step for an \(S_N1\) reaction.
Carbocation stability
What, then, are the characteristics of an electrophile that favor an \(S_N1\) reaction pathway as opposed to an \(S_N2\) pathway? We know that the rate-limiting step of an \(S_N1\) reaction is the first step: loss of the leaving group and formation of the carbocation intermediate. Accordingly, the rate of an \(S_N1\) reaction depends to a large extent on the stability of the carbocation intermediate.
The critical question now becomes:
What stabilizes a carbocation?
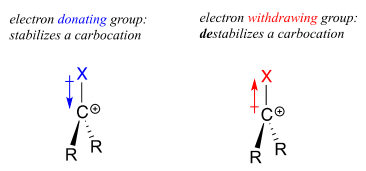
Think back to Chapter 7, when we were learning how to evaluate the strength of an acid. The critical question there was: “how stable is the conjugate base that results when this acid donates its proton”? In many cases, this conjugate base was an anion – a center of excess electron density. Anything that can draw some of this electron density away– in other words, any electron withdrawing group – will stabilize the anion.
Conversely, a carbocation is stabilized by an electron donating group, and destabilized by an electron withdrawing group.
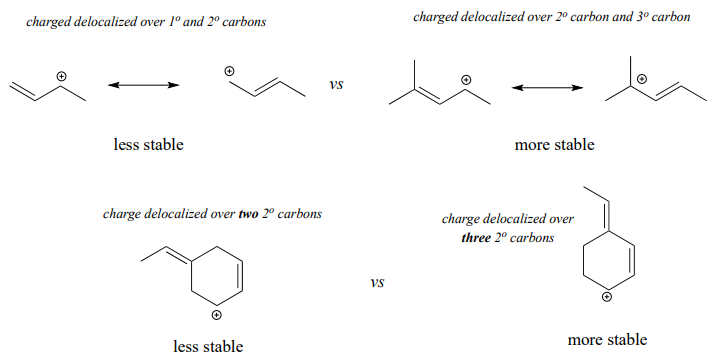
A positively charged species such as a carbocation is electron-poor, and thus anything which donates electron density to the center of electron poverty will help to stabilize it. Alkyl groups, because of the electrons in their carbon-carbon and carbon-hydrogen bonds, are weak electron-donating groups, and will stabilize nearby carbocations. What this means is that, in general, more substituted carbocations are more stable: a tert-butyl carbocation, for example, is more stable than an isopropyl carbocation. Primary carbocations are highly unstable and not often observed as reaction intermediates; methyl cations are even less stable.
More substituted carbocations are more stable:
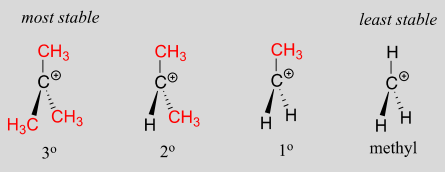
Another way to explain this trend in carbocation stability involves the phenomenon of hyperconjugation, in which the empty \(p\) orbital of a carbocation is stabilized by overlap with a \(\sigma\) bond on an adjacent carbon. This overlap effectively spreads the positive charge over a larger area. The figure below shows the empty \(p\) orbital of a secondary carbocation being stabilized by hyperconjugation with an adjacent \(C-H \) \(\sigma \) bond.
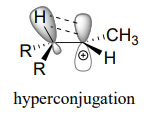
Hyperconjugation is not possible with a methyl cation as there is no adjacent \(\sigma\) bond available to overlap the empty \(p\) orbital. As the degree of substitution on a carbocation increases, so does the capacity for stabilizing hyperconjugation interactions.
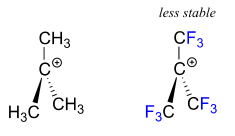
The presence of an electron-withdrawing group - such as a fluorine atom - will significantly destabilize a carbocation through the inductive effect.
Carbonyl groups are electron-withdrawing by inductive effects, due to the polarity of the \(C=O\) double bond. It is possible to demonstrate in the laboratory (we'll see how in problem 14.x) that carbocation A below is more stable than carbocation B, even though A is a primary carbocation and B is secondary.
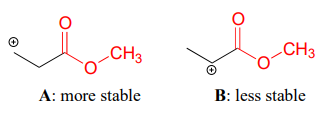
The positive charge in cation B is closer to the electron withdrawing carbonyl substitution, and as we learned in section 7.3, the inductive effect of an electron withdrawing group decreases with distance.
Stabilization of a carbocation can also occur through resonance effects. Recall from section 7.4 that the negative charge on a phenolate ion is stabilized by resonance, because the charge can be delocalized to three of the carbons on the aromatic ring.
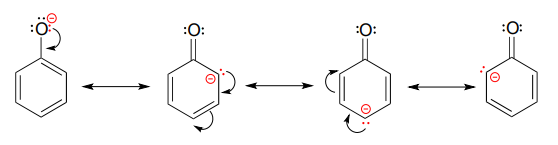
A positive charge is also stabilized when it can be delocalized over more than one atom. Consider a benzylic carbocation, where the positively-charged carbon is bonded directly to an aromatic ring. A benzylic carbocation is stabilized by the resonance electron-donating effect of the aromatic ring. Three additional resonance structures can be drawn for the carbocation in which the positive charge is located on one of three aromatic carbons:
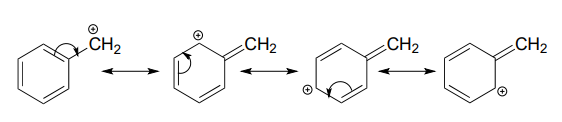
Fill in the missing numbers in this statement: The conjugated \(p\) system in the benzylic carbocation above is composed of ______ \(p\) orbitals overlapping to share ______ \(\pi \) electrons.
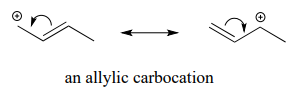
Allylic carbocations, where the positively charged carbon is adjacent to a double bond, are stabilized by resonance delocalization of the posive charge.
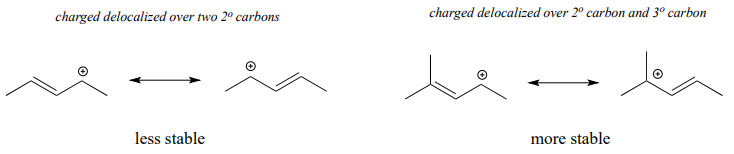
Often, we must consider more than one factor when predicting carbocation stability. For example, the carbocation on the right in the figure below is more stable than the carbocation on the left. Both are allylic with the charge delocalized over two carbons, but on the more stable carbocation, one of the carbons is tertiary.
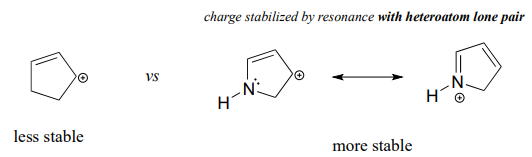
Because heteroatoms such as oxygen and nitrogen are more electronegative than carbon, you might expect that they would be carbocation-destabilizing electron withdrawing groups. In fact, the opposite is often true: if the oxygen or nitrogen atom is in the right position, the overall effect can be carbocation stabilization. Although these heteroatoms are indeed electron withdrawing groups by induction, they can be electron donating groups by resonance, and, as we learned earlier (section 7.3) in the context of acid-base chemistry, resonance effects are in general more powerful than inductive effects when the two operate in opposite directions.
Consider the two pairs of carbocation species below:
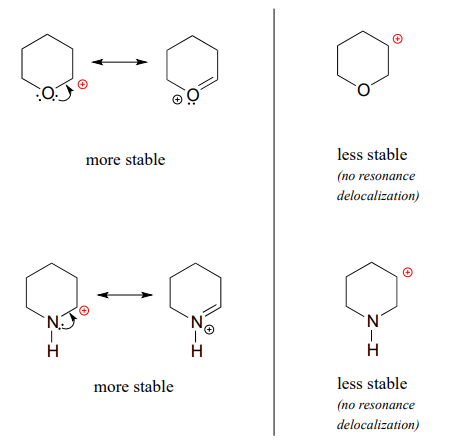
In the more stable carbocations, the heteroatom acts as an electron donating group by resonance: in effect, the lone pair on the heteroatom is available to delocalize the positive charge. Note also that every atom in the major resonance contributor has a complete octet of valence electrons.
Rank the following carbocations from most to least stable:
Finally, vinylic carbocations, in which the positive charge resides on a double-bonded carbon, are highly unstable.
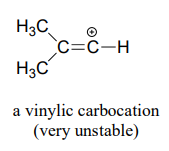
Explain why vinylic carbocations are unstable. (Hint: )
- Hint
-
Think about hybridization and electronegativity.
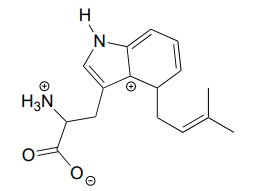
The carbocation below is an intermediate species in a reaction that is part of the biosynthesis of a hallucinogenic compound in a fungus. Draw a resonance contributor that shows how it is stabilized by resonance with the nitrogen atom.
For the most part, carbocations - even 'relatively stable' carbocations such as those that are tertiary and/or benzylic - are still highly reactive, transient intermediate species in organic reactions, which briefly form and then react again right away. However, there are some unusual examples of carbocation species that are so stable that they can be put in a jar and stored on the shelf as a salt. Crystal violet is the common name for the chloride salt of the carbocation whose structure is shown below. Notice the structural possibilities for extensive resonance delocalization of the positive charge, and the presence of three electron-donating amine groups.
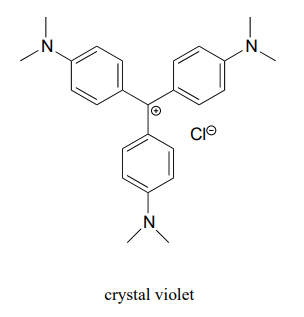
- Draw a resonance structure of the crystal violet cation in which the positive charge is delocalized to one of the nitrogen atoms.
- Notice that crystal violet is deeply colored. Explain why you could have predicted this from looking at its chemical structure.
- The conjugated system of crystal violet consists of how many overlapping p orbitals sharing how many p electrons?
- More substituted carbocations are more stable than less substituted carbocation (eg. tertiary carbocations are more stable than secondary carbocations).
- Nearby electronegative atoms can decrease carbocation stability by the inductive effect.
- Allylic and benzylic carbocations are stabilized by resonance delocalization of the positive charge .
- Delocalization of the positive charge by resonance with the lone pair electrons on a heteroatom contributes to carbocation stability.
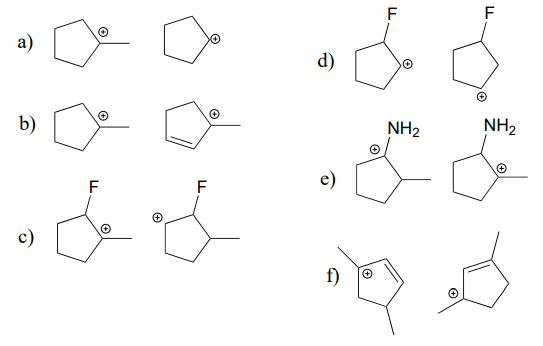
Below are three examples illustrating how we can make predictions about relative carbocation stability:
State which carbocation in each pair below is more stable, or if they are expected to be approximately equal. Explain your reasoning.
Now, back to our discussion of the electrophile in an \(S_N1\) reaction:
An \(S_N1\) reaction requires a stabilized carbocation intermediate. The more stable the relevant carbocation intermediate, the more favored the \(S_N1\) reaction pathway.
\(S_N1\) reactions in general do not occur at methyl or primary carbon electrophiles: the carbocation intermediates involved would be too unstable and the rate-determining (carbocation-generating) step would have a very high energy barrier. Substitution on these electrophiles will occur through the \(S_N2\) pathway.
The \(S_N1\) reaction pathway is possible, however, with secondary and tertiary carbon electrophiles, or with any other carbon electrophile in which departure of the leaving group generates a carbocation which is stabilized by resonance.
For example: a primary alkyl bromide would not be expected to undergo nucleophilic substitution by the \(S_N1 \)pathway. An allylic primary alkyl bromide, on the other hand, would generate a relatively stable allylic carbocation and thus the \(S_N1\) pathway is possible.
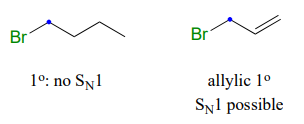
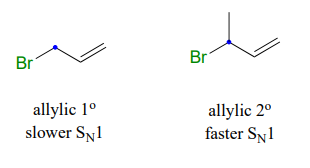
An allylic secondary alkyl bromide would undergo \(S_N1\) substitution more rapidly than the allylic primary alkyl bromide, because the relevant carbocation is more substituted and thus more stable.
\(sp^2\)-hybridized carbons
Nucleophilic substitution generally does not occur at \(sp^2\)-hybridized carbons, either by the \(S_N2\) or \(S_N1\) pathway.
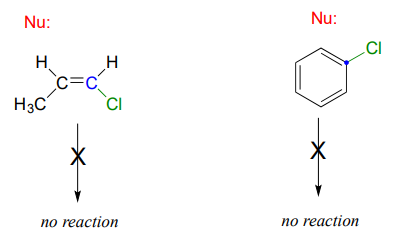
Bonds on \(sp^2\)-hybridized carbons are inherently shorter and stronger than bonds on \(sp^3\)-hybridized carbons, meaning that it is harder to break the bond between an \(sp^2\) carbon and a potential leaving group (such as the chlorine atom in the figure above). In addition, steric considerations play a part here: in order to attack from behind the leaving group in an \(S_N2\)-like fashion, the nucleophile would need to approach in the plane of the carbon-carbon double bond.
Substitution by an \(S_N1\) pathway is equally unlikely because of the inherent instability of a vinylic (double-bonded) carbocation.


