8.9: The E2 Reaction

Kinetics and Mechanism

The conditions used for substitution reactions by the \(\text{S}_\text{N}2\) mechanism very often lead to elimination. The reaction of 2-bromopropane with sodium ethoxide in ethanol provides a good example:

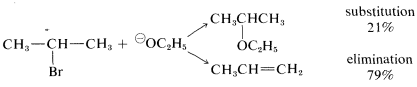
Elimination to give propene competes with substitution to give ethyl isopropyl ether. Furthermore, the rate of elimination, like the rate of substitution, is proportional to the concentrations of 2-bromopropane and ethoxide ion. Thus elimination here is a second-order reaction (it may be helpful to review Section 8-4 at this point):

rate of substitution \(= k_S \left[ R Br \right] \left[ \overset{\ominus}{O} C_2H_5 \right]\)

rate of elimination \(= k_E \left[ R Br \right] \left[ \overset{\ominus}{O} C_2H_5 \right]\)

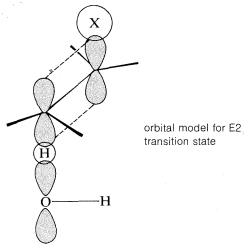
As to the mechanism of this kind of elimination, the attacking base, \(^\ominus OC_2H_5\), removes a proton from the \(\beta\) carbon more or less simultaneously with the formation of the double bond and the loss of bromide ion from the neighboring carbon:

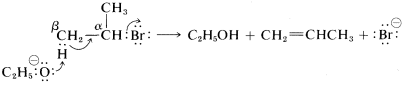
The abbreviation for this mechanism is \(\text{E}2\), \(\text{E}\) for elimination and \(2\) for bimolecular, there being two reactants involved in the transition state.

Structural Effects

Structural influences on \(\text{E}2\) reactions have been studied in some detail. Like the competing \(\text{S}_\text{N}2\) process, a good leaving group is necessary and of these, the most commonly used are the halides, \(Cl\), \(Br\), and \(I\); sulfonate esters, \(RS \left( O_2 \right) O-\); and -onium ions such as ammonium, \(\overset{\oplus}{N} R_4\), and sulfonium, \(\overset{\oplus}{S} R_3\):

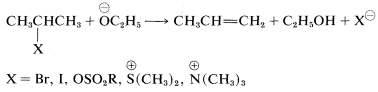
Rather strong bases generally are required to bring about the \(\text{E}2\) reaction. The effectiveness of a series of bases generally parallels their base strengths, and the order \(\overset{\ominus}{N} H_2\) \(>\) \(\overset{\ominus}{O} C_2H_5\) \(>\) \(\overset{\ominus}{O} H\) \(>\) \(\overset{\ominus}{O} CCH_3\) is observed for \(\text{E}2\) reactions. This fact is important in planning practical syntheses, because the \(\text{E}2\) reaction tends to predominate with strongly basic, slightly polarizable reagents such as amide ion, \(\overset{\ominus}{N} H_2\), or ethoxide ion, \(\overset{\ominus}{O} C_2H_5\). In contrast, \(\text{S}_\text{N}2\) reactions tend to be favored with weakly basic nucleophiles such as iodide ion or ethanoate ion (unless dipolar aprotic solvents are used, which may markedly change the reactivity of anionic nucleophiles).

As for the alkyl group, there are two important structural effects to notice. First, at least one \(C-H\) bond adjacent (\(\beta\)) to the leaving group is required. Second, the ease of \(\text{E}2\) elimination follows the order tertiary \(R\) \(>\) secondary \(R\) \(>\) primary \(R\). Unlike \(\text{S}_\text{N}2\) reactions, which are not observed for tertiary alkyl compounds because of steric hindrance to the approach of the nucleophile to carbon, the related \(\text{E}2\) reaction usually occurs readily with tertiary \(RX\) compounds. The reason is that little or no steric hindrance is likely for the approach of a base to a hydrogen unless the base is exceptionally bulky:

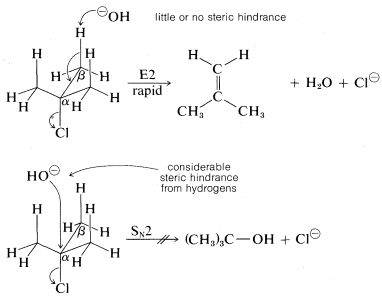
The reactivity order also appears to correlate with the \(C-X\) bond energy, inasmuch as the tertiary alkyl halides both are more reactive and have weaker carbon-halogen bonds than either primary or secondary halides (see Table 4-6). In fact, elimination of \(HX\) from haloalkenes or haloarenes with relatively strong \(C-X\) bonds, such as chloroethene or chlorobenzene, is much less facile than for haloalkanes. Nonetheless, elimination does occur under the right conditions and constitutes one of the most useful general methods for the synthesis of alkynes. For example,

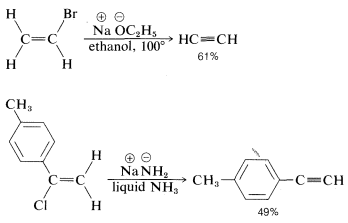
The conditions and reagents used for \(\text{E}2\) and \(\text{S}_\text{N}2\) reactions are similar enough that it is difficult to have one occur without the other. However, \(\text{E}2\) elimination is favored over \(\text{S}_\text{N}2\) substitution by (a) strongly basic nucleophiles, (b) bulky nucleophiles, and (c) increasing alkyl substitution at the \(\alpha\) carbon. It also is observed that increasing the reaction temperature generally leads to an increase in elimination at the expense of substitution. In fact, surprisingly good yields of alkene or alkyne can be obtained by adding a halogen compound directly to molten or very hot \(KOH\) with no solvent present, whereupon the product is formed rapidly and distills immediately from the hot reaction mixture:

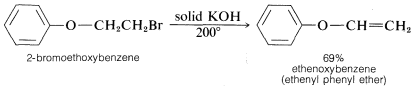
Orientation Effects in Elimination Reactions

With halides having unsymmetrical \(R\) groups, such as 2-chloro-2-methylbutane, it is possible to form two or more different alkenes, the proportion depending on the relative rates at which the different \(\beta\) hydrogens are removed. Most \(\text{E}2\) eliminations of alkyl halides with common bases, such as \(HO^\ominus\), \(C_2H_5O^\ominus\), and \(NH_2^\ominus\), tend to give mixtures of alkenes with a preference for the most stable alkene, which usually is the one with the fewest hydrogens or most alkyl groups attached to the carbons of the double bond. Thus

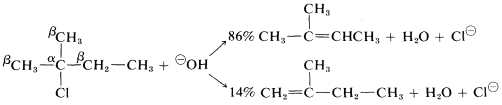
However, the precise distribution of alkenes formed is found to vary enough with the nature of the leaving group, or the base used, so either product will predominated with some combination of reagents or conditions. For example, a change in the base alone can be decisive:

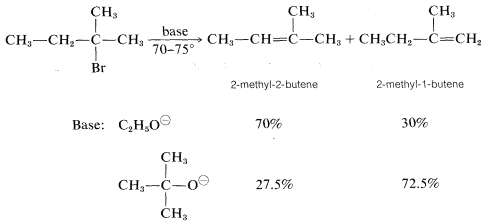
Stereochemistry of \(\text{E}2\) Reactions

The \(\text{E}2\) reaction occurs most easily if the molecule undergoing reaction can assume a conformation, \(2\), in which the leaving groups, \(H\) and \(X\), are trans to each other and the atoms \(H-C_\beta-C_\alpha-X\) lie in one plane. Elimination then proceeds from opposite sides of the incipient double bond to give an alkene of structure \(3\). We shall call this mode of elimination antarafacial to distinguish

Figure 8-6: Schematic representation of antarafacial (literally "opposite-face") and suprafacial (literally "above-face") elimination or addition of a reagent \(X-Y\) to ethene

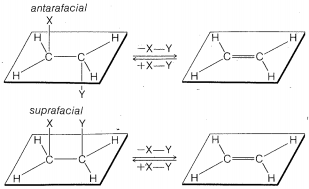
it from another possible mode of elimination that is called suprafacial. (See Figure 8-6).\(^8\)

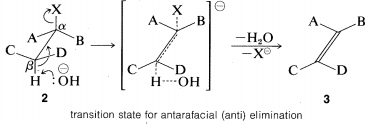
The transition state for conversion of \(2\) to \(3\) is particularly reasonable because it combines some of the geometry of both the reactants and the products and therefore gives the best overlap of the reacting orbitals necessary for the formation of the \(\pi\) bond. This is shown more explicitly below.\(^9\)

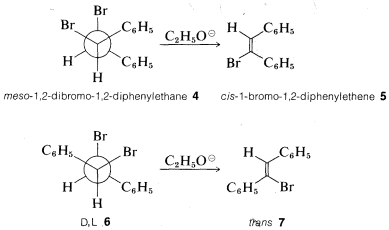
As an illustration of the stereospecificity of eliminations, the meso compound \(4\) gives the cis-alkene \(5\), whereas the \(D,L\) isomers \(6\) give the trans-alkene \(7\) with ethoxide. Both reactions clearly proceed by antarafacial elimination:

When antarafacial elimination is rendered difficult by the inability of the reacting groups to acquire the desired trans arrangement, then suprafacial elimination can occur, although less readily. An example is chlorocyclopentane, in which \(H\) and \(X\) cannot assume a trans configuration without very considerable strain but which does undergo suprafacial elimination at a reasonable rate:

Figure 8-6. At the risk of annoying those who often rightly dislike complicated names for simple processes, we have chosen to adopt the proposal of R. B. Woodward and R. Hoffman, that elimination (or addition) which involves a same-side cleavage (or formation) of bonds be called suprafacial and the opposite-side cleavage (or formation) of bonds be called antarafacial. The alternative of using syn for suprafacial and anti for antarafacial would be simpler and easier to remember, but the terms syn and anti already are used for configurations, which is exactly what we want to avoid. The problem with the terms cis elimination (or addition) and trans elimination (or addition) is that they do not necessarily lead to products that, by other conventions, are understood to be cis and trans products, respectively, For example, to say that "trans elimination leads to cis product" is a needless confusion. It is much clearer to say that "antarafacial elimination gives the cis product" - and now there is no confusion of the mode of elimination with whatever stereochemical convention identifies the product.

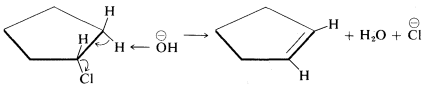
\(^9\)Persuasive arguments have been made that many \(\text{E}2\) reactions proceed by the sequence

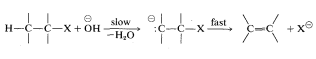
If this is so, antarafacial elimination still is predicted to be favored.

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."