8.8: Structural and Solvent Effects in \(S_N\) Reactions
- Page ID
- 22217
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We shall consider first the relationship between the structures of alkyl derivatives and their reaction rates toward a given nucleophile. This will be followed by a discussion of the relative reactivities of various nucleophiles toward a given alkyl derivative. Finally, we shall comment in more detail on the role of the solvent in \(\text{S}_\text{N}\) reactions.
Structure of the Alkyl Group, \(R\), in \(\text{S}_\text{N}2\) Reactions
The rates of \(\text{S}_\text{N}2\)-displacement reactions of simple alkyl derivatives, \(RX\), follow the order primary \(R\) \(>\) secondary \(R\) \(\gg\) tertiary \(R\). In practical syntheses involving \(\text{S}_\text{N}2\) reactions, the primary compounds generally work very well, secondary isomers are fair, and the tertiary isomers are almost completely impractical. Steric hindrance appears to be particularly important in determining \(\text{S}_\text{N}2\) reaction rates, and the slowness of tertiary halides seems best accounted for by steric hindrance to the back-side approach of an attacking nucleophile by the alkyl groups on the reacting carbon. Pertinent data, which show how alkyl groups affect \(\text{S}_\text{N}2\) reactivity toward iodide ion, are given in Table 8-1. Not only do alkyl groups suppress reactivity when on the same carbon as the leaving group \(X\), as in tert-butyl bromide, but they also have retarding effects when located one carbon away from the leaving group. This is evident in the data of Table 8-1 for 1-bromo-2,2-dimethylpropane (neopentyl bromide), which is very unreactive in \(\text{S}_\text{N}2\) reactions. Scale models indicate the retardation to be the result of steric hindrance by the methyl groups located on the adjacent \(\beta\) carbon to the approaching nucleophile:

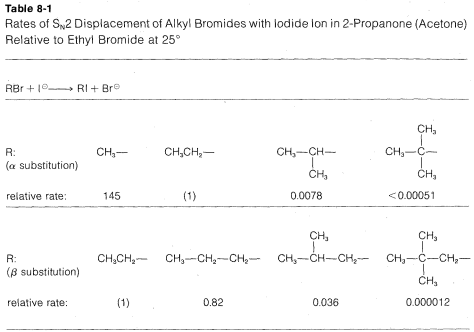
In addition to steric effects, other structural effects of \(R\) influence the \(\text{S}_\text{N}2\) reactivity of \(RX\). A double bond \(\beta\) to the halogen,\(^6\) as in 2-propenyl, phenylmethyl (benzyl), and 2-oxopropyl chlorides enhances the reactivity of the compounds toward nucleophiles. Thus the relative reactivities toward \(I^\ominus\) in 2-propanone are
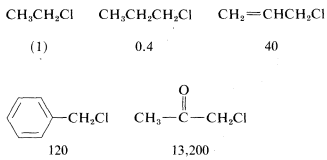
Possible reasons for these high reactivities will be discussed later (Section 14-3B).
Structure of the Alkyl Group, \(R\), in \(\text{S}_\text{N}1\) Reactions
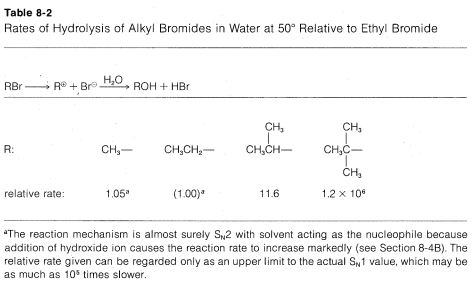
The rates of \(\text{S}_\text{N}1\) reactions of simple alkyl derivatives follow the order tertiary \(R\) \(\gg\) secondary \(R\) \(>\) primary \(R\), which is exactly opposite that of \(\text{S}_\text{N}2\) reactions. This is evident from the data in Table 8-2, which lists the relative rates of hydrolysis of some alkyl bromides; only the secondary and tertiary bromides react at measurable rates, and the tertiary bromide reacts some \(10^5\) times faster than the secondary bromide.
Why do tertiary alkyl compounds ionize so much more rapidly than either secondary or primary compounds? The reason is that tertiary alkyl cations are more stable than either secondary or primary cations and therefore are formed more easily. You will appreciate this better by looking at the energy diagram of Figure 8-4, which shows the profile of energy changes for hydrolysis of an alkyl compound, \(RX\), by the \(\text{S}_\text{N}1\) mechanism. The rate of
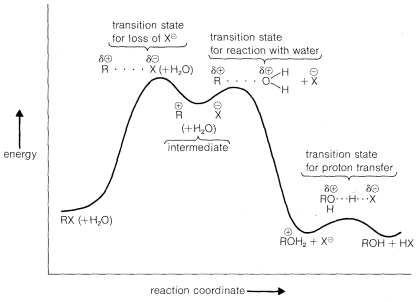
reaction is determined by the ionization step, or by the energy of the transition state relative to that of the reactants. Actually, the energy of the transition state is only slightly higher than the energy of the ionic intermediates \(R^\oplus X^\ominus\). Thus to a first approximation, we can say that the rate of ionization of \(RX\) will depend on the energies of the ions formed. Now if we compare the rates for a series of compounds, \(RX\), all having the same leaving group, \(X\), but differing only in the structure of \(R\), their relative rates of ionization will correspond to the relative stabilities of \(R^\oplus\). The lower energy of \(R^\oplus\), the faster will be the rate of ionization. Therefore the experimental results suggest that the sequence of carbocation stabilities is tertiary \(R^\oplus\) \(\gg\) secondary \(R^\oplus\) \(\gg\) primary \(R^\oplus\).
Just why this sequence is observed is a more difficult question to answer. Notice in the following stability sequence that alkyl cations are more stable the more alkyl groups there are on the positive carbon:

The simplest explanation for why this is so is that alkyl groups are more polarizable than hydrogens. In this case, more polarizable means the electrons of the alkyl groups tend to move more readily toward the positive carbon than do those of the hydrogens. Such movements of electrons transfer part of the charge on the cationic carbon to the alkyl groups, thereby spreading the charge over a greater volume. This constitutes electron delocalization, which results in enhanced stability (see Section 6-5A).
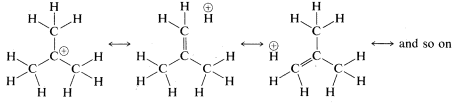
An alternative way of explaining how the cationic charge is spread over the alkyl groups of a tertiary cation, such as the tert-butyl cation, is to write the cation as a hybrid of the following structures:
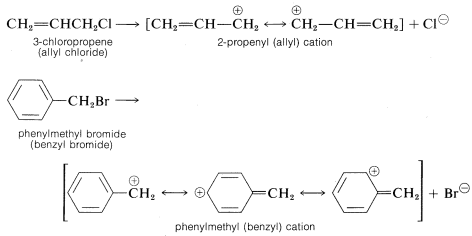
Other organohalogen compounds besides secondary and tertiary alkyl compounds can react by \(\text{S}_\text{N}1\) mechanisms provided they have the ability to form reasonably stabilized carbon cations. Examples include 2-propenyl (allylic) and phenylmethyl (benzylic) compounds, which on ionization give cations that have delocalized electrons (see Section 6-6):
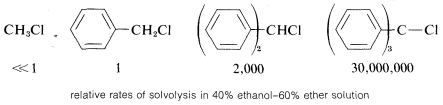
In general, the more stabilized the carbon cation from an alkyl halide, the more reactive the compound will be in \(\text{S}_\text{N}1\)-type reactions. This is especially apparent in the reactivities of compounds with phenyl groups on the reacting carbon. As the number of phenyl groups increases from zero to three, the \(\text{S}_\text{N}1\) reactivity of the chlorides increases by more than \(10^7\) because of increasing stabilization of the carbon cation by the phenyl groups:
In contrast, compounds such as chlorobenzene and chloroethene, in which the halogen is attached directly to a multiply bonded carbon atom, do not exhibit \(\text{S}_\text{N}1\)-type reactions. Evidently then, unsaturated carbon cations such as phenyl or ethenyl are appreciably less stable (more difficult to form) than tert-alkyl cations:

Reasons for this will be considered in Section 14-4B.
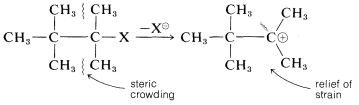
Steric hindrance is relatively unimportant in \(\text{S}_\text{N}1\) reactions because the rate is independent of the nucleophile. In fact, steric acceleration is possible in the solvolysis of highly branched alkyl halides through relief of steric compression between the alkyl groups in the halide by formation of a planar cation:
Along with the effect \(R\) has on the rate at which an alkyl compound \(RX\) reacts by an \(\text{S}_\text{N}1\) mechanism, the group \(R\) also affects the nature of the products obtained. The intermediate alkyl cations \(R^\oplus\) may react in various ways to give products of substitution, elimination, and rearrangement. Elimination pathways are discussed more fully starting in Section 8-8, and rearrangement of carbon cations in Section 8-9B.
The Leaving Group
The reactivity of a given alkyl derivative, \(RX\), in either \(\text{S}_\text{N}1\) or \(\text{S}_\text{N}2\) reactions, is influenced strongly by the leaving group, \(X\). The choice of leaving group is therefore an important consideration in any synthesis involving \(\text{S}_\text{N}\) reactions.
From the foregoing discussion of structural effects in the \(R\) group on \(\text{S}_\text{N}\) reactivity, particularly in \(\text{S}_\text{N}1\) reactions, we might expect the stability of \(:X\) as an ion or neutral molecule to play a major role in determining how good or poor \(X\) is as a leaving group. The stability of \(:X\) is indeed important - the problem is that there are several factors that contribute to the stavility and hence the lability of the leaving group.
For the purpose of initially identifying good and poor leaving groups, consider development of a practical synthesis of diethyl ether. One route is by way of \(\text{S}_\text{N}2\) displacement using an ethyl compound, \(CH_3CH_2X\), and ethoxide ion:
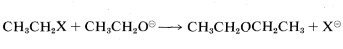
Many \(CH_3CH_2X\) compounds have \(X\) groups that are quite unsatisfactory in this reaction. They include compounds such as ethane, propane, ethanol, ethyl methyl ether, ethylamine, and ethyl ethanoate; the respective groups, \(H^\ominus\), \(CH_3^\ominus\), \(HO^\ominus\), \(CH_3O^\ominus\), \(NH_2^\ominus\), and \(CH_3CO_2^\ominus\) all can be classified as very poor leaving groups. The more reactive ethyl derivatives (see Table 8-3) include the halides, particularly ethyl iodide, and sulfonic acid derivatives; the corresponding anions \(Cl^\ominus\), \(Br^\ominus\), \(I^\ominus\), and \(RS \left( O_2 \right) O^\ominus\) therefore are moderate to good leaving groups. Table 8-3 includes pertinent data for the rates of ether formation from various alkyl compounds and illustrates that the relative abilities of groups to leave are about the same in \(\text{S}_\text{N}1\) reactions as they are in \(\text{S}_\text{N}2\) reactions.
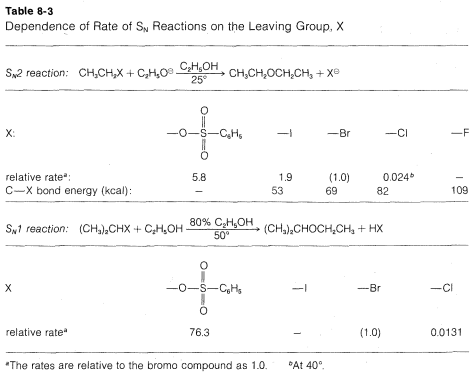
Why are groups such as \(I^\ominus\) and \(RSO_3^\ominus\) good leaving groups, whereas others such as \(H^\ominus\), \(HO^\ominus\) and \(NH_2^\ominus\) are poor? The simplest correlation is with the strength of \(HX\) as an acid. This is very reasonable because the ease of loss of \(X^\ominus\), as from \(\left( CH_3 \right) C-X\) in an \(\text{S}_\text{N}1\) reaction, would be expected to be related, to some degree at least, to the ease of ionization of \(H-X\) to \(H^\oplus\) and \(X^\ominus\). Therefore the stronger \(HX\) is as an acid, the better \(X\) will be as a leaving group. Thus \(HF\) is a relatively weak acid and \(F^\ominus\) is not a very good leaving group; \(H-I\) is a very strong acid and \(I^\ominus\) is a good leaving group. The usual order of reactivity of alkyl halides, \(R-I\) \(>\) \(R-Br\) \(>\) \(R-Cl\) \(>\) \(R-F\) (when \(R\) is the same group throughout), is in accord with the acid strengths of the halogen acids. SImilarly, \(CF_3CO_2-\) is a much better leaving group than \(CH_3CO_2-\), and we find that trifluoroethanoic acid, \(CF_3CO_2H\) is a several thousand times stronger acid than ethanoic acid, \(CH_3CO_2H\). For the same reason, \(CF_3SO_3^\ominus\) is a better leaving group than \(CH_3XO_3^\ominus\).
This correlation can be extended easily to groups that leave as neutral \(X:\). For example, \(ROH_2^\oplus \rightarrow R^\oplus + H_2O\) occurs far more readily than \(ROH \rightarrow R^\oplus + OH^\ominus\) and we know that \(H_3O^\oplus\) is a stronger acid (or better proton donor) than \(H_2O\).
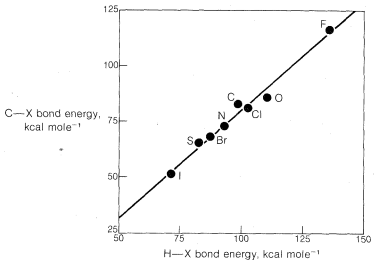
The relationship between \(X^\ominus\) as a leaving group and \(HX\) as an acid is very useful because much information is available on acid strengths. However, it is not a very fundamental explanation unless we can explain why some acids are strong acids and others are weak acids. One factor is the strength of the \(H-X\) bond, but here we need to remember that the usual bond strengths are for dissociation to radicals or atoms, not ions, and for the gas, not for solutions. If we write the steps relating the bond-dissociation energy to the energy of ionic dissociation in solution, we see that for variations in \(X\), in addition to the bond energy, the electron affinity of \(X \cdot\), the solvation energy of \(X^\ominus\), and the solvation energy of \(HX\), also will be contributing factors.

Enhancement of Leaving Group Abilities by Electrophilic Catalysis
In general, a leaving group that leaves as a neutral molecule is a much better leaving group than one that leaves as an anion. Alcohols, \(ROH\), are particularly unreactive in \(\text{S}_\text{N}\) reactions because \(OH^\ominus\) is a very poor leaving group. However, if a strong acid is present, the reactivity of the alcohol is enhanced greatly. The acid functions by donating a proton to the oxygen of the alcohol, thereby transforming the hydroxyl function into \(ROH_2^\oplus\), which has a much better leaving group, \(H_2O\), in place of \(OH^\ominus\). The \(\text{S}_\text{N}\) reactions of ethers and esters are acid-catalyzed for the same reason.
Heavy-metal salts, particularly those of silver, mercury, and copper, catalyze \(\text{S}_\text{N}1\) reactions of alkyl halides in much the same way that acids catalyze the \(\text{S}_\text{N}\) reactions of alcohols. A heavy-metal ion functions by complexing with the unshared electrons of the halide, thereby making the leaving group a metal halide rather than a halide ion. This acceleration of the rates of halide reactions is the basis for a qualitative test for alkyl halides with silver nitrate in ethanol solution:
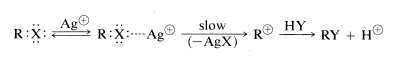
Silver halide precipitates at a rate that depends upon the structure of the alkyl group, tertiary \(>\) secondary \(>\) primary. Tertiary halides usually react immediately at room temperature, whereas primary halides require heating. That complexes actually are formed between organic halides and silver ion is indicated by an increase in water solubility in the presence of silver ion for those halides that are slow in forming carboncations.
The Nucleophilic Reagent
The nucleophilicty of a particular reagent (\(:Y\), \(:Y^\ominus\), or \(H \ddot{Y}\)) can be defined as its ability to donate an electron pair to another atom (see Section 8-1). In fact, the \(\text{S}_\text{N}2\) reactivity of a reagent toward a methyl derivative can be taken to measure its nucleophilicty toward carbon. The relative reaction rates of some nucleophiles toward methyl bromide are listed in order of increasing nucleophilicity in Table 8-4, together with their basicities as measured by \(K_b\). Important generalizations can be made from these data provided that one recognizes that they may apply only to hydroxylic solvents.
1. For the atoms representing any one group (column) of the periodic table, nucleophilicty increases with increasing atomic number: \(I^\ominus\) \(>\) \(Br^\ominus\) \(>\)
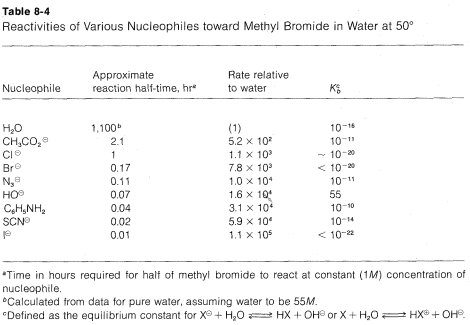
\(Cl^\ominus\) \(>\) \(F^\ominus\); \(HS^\ominus\) \(>\) \(HO^\ominus\); \(PH_3\) \(>\) \(NH_3\). Thus, other things being equal, larger atoms are better nucleophiles.
2. For nucleophiles having the same atomic number of the entering atom (e.g., oxygen nucleophiles), there is usually a good correlation between the basicity of the reagent and its nucleophilicity. Thus a weak base such as \(CH_3CO_2^\ominus\) is a poorer nucleophile than a strong base such as \(^\ominus OH\). The poorer \(X^\ominus\) is as a leaving group, the better it is as an entering group.
3. For nucleophiles of different atomic numbers, nucleophilicity usually does not parallel basicity. For example, for the halogens the reactivity sequence \(I^\ominus\) \(>\) \(Br^\ominus\) \(>\) \(Cl^\ominus\) is opposite to the sequence for basicity \(Cl^\ominus\) \(>\) \(Br^\ominus\) \(>\) \(I^\ominus\). Similarly, sulfur anions such as \(HS^\ominus\) are better nucleophiles but weaker bases than corresponding oxyanions such as \(HO^\ominus\).
4. A number of nucleophilic agents, which are very reactive in \(\text{S}_\text{N}2\) reactions, are of the type \(X-Y\), where both atoms have unshared electron pairs. Examples include \(HOO^\ominus\), \(H_2NO^\ominus\), \(ClO^\ominus\), and \(H_2NNH_2\), all of which are more reactive than the closely related nucleophiles \(HO^\ominus\) and \(NH_3\).
Why is the correlation between basicity and nucleophilcity so poor for atoms of different atomic number? it is now clear from much research that the dominant effect is associated with differences in the solvation energies of the ions, as defined for halide ions by the following equations:
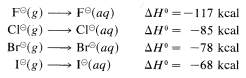
The solvation energies of small ions with concentrated charge always are greater than those of large ions with diffuse charge.
When an ion participates in a nucleophilic attack on carbon, it must slough off some of the solvent molecules that stabilize it in solution. Otherwise, the ion cannot get close enough to the carbon, to which it will become attached, to begin forming a bond. Sloughing off solvent molecules will be less favorable for a small ion than a large ion. Consequently, we expect \(Cl^\ominus\) to be less reactive than \(I^\ominus\).
Strong evidence for solvation effects on reactivity is provided by the fact that chloride ion is more reactive than iodide in solvents that have low solvation energies for anions (see Section 8-7F). Furthermore, in the gas phase where solvation effects are absent, \(F^\ominus\) is more reactive than any of the other halide ions toward chloromethane:
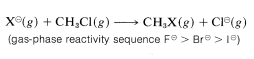
It should be recognized that \(\text{S}_\text{N}\) reactions may be reversible when both the leaving group \(X\) and the entering group \(Y\) are good entering and leaving groups, respectively. In such circumstances, the position of the equilibrium often can be changed by suitably adjusting the reaction conditions. Thus \(48\%\) aqueous hydrogen bromide can convert alcohols to alkyl bromides (Equation 8-6, forward direction), whereas the reverse reaction (hydrolysis) is achieved by high water concentration:

The Nature of the Solvent
The rates of \(\text{S}_\text{N}\) reactions are sensitive to the nature and composition of the solvent. This is easy to understand for \(\text{S}_\text{N}1\) reactions because the ionizing power of a solvent is crucial to the ease of formation of ions \(\overset{\oplus}{R}\) and \(\overset{\ominus}{X}\) from \(RX\).
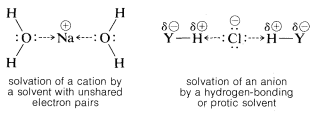
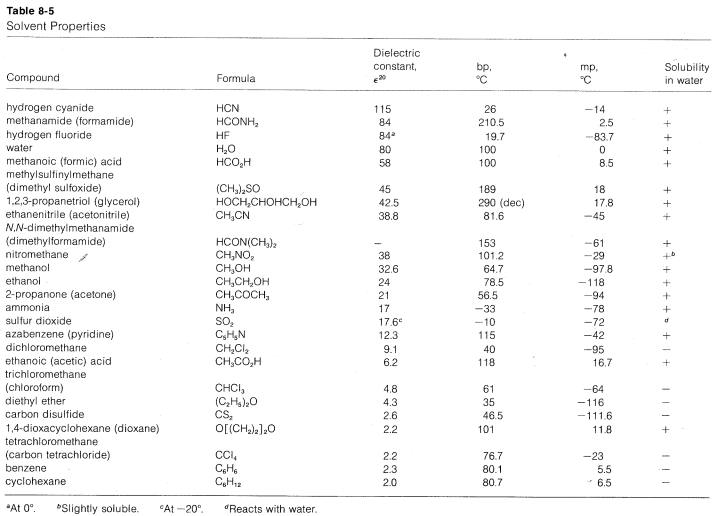
Actually, two factors are relevant in regard to the ionizing ability of solvents. First, a high dielectric constant increases ionizing power by making it easier to separate ions. This is because the force between charged particles varies inversely with the dielectric constant of the medium.\(^7\) Thus water, with a dielectric constant of 80, is 40 times more effective than a hydrocarbon with a dielectric constant of 2. Second, and usually more important, is the ability of the solvent to solvate the separated ions. Cations are solvated most effectively by compounds of elements in the first row of the periodic table that have unshared electron pairs. Examples are ammonia, water, alcohols, carboxylic acids, sulfur dioxide, and methylsulfinylmethane [dimethyl sulfoxide, \(\left( CH_3 \right)_2 SO\)]. Anoins are solvated most efficiently by solvents having hydrogen attached to a strongly elecronegative element \(Y\) so the \(H-Y\) bond is strongly polarized as \(\overset{\delta \oplus}{H} \: \cdot \: \cdot \: \cdot \: \overset{\delta \ominus}{Y}\). Such solvents usually are called protic solvents. Protic solvents form hydrogen bonds to the leaving group, which assist ionization in much the same way that silver ion catalyzes ionization of alkyl halides (Section 8-7D). We can represent solvation by the following structural formulas, but it must be recognized that the number of solvent molecules involved in close interacitons can be as large as four or six, or as small as one:
The most effective ionizing solvents are those that effectively solvate both anions and cations. Water strikes an excellent compromise with regard to the structural features that make up ionizing power, that is, dielectric constant and solvating ability. From this, we expect tert-butyl chloride to ionize much more readily in water than in ether, because ethers can solvate only cations effectively, whereas water can solvate both anions and cations. The fact is that \(\text{S}_\text{N}1\) ionizations usually are so difficult that \(\text{S}_\text{N}1\) reactions seldom occur in solvents that cannot effectively solvate both anions and cations, even if the dielectric constant of the solvent is high. Solvation by hydrogen bonding is especially helpful in assisting ionization. Solvents that cannot provide such hydrogen bonding [e.g., \(CH_3OCH_3\), \(\left( CH_3 \right)_3 N\), \(CH_3NO_2\), \(CH_3CN\), \(\left( CH_3 \right)_2 SO\)] generally are poor for \(\text{S}_\text{N}1\) reactions. These solvents are called aprotic solvents. An important exception is liquid sulfur dioxide, \(SO_2\), which promotes \(\text{S}_\text{N}1\) ionization by having a high dielectric constant and being able to solvate both anions and cations.
A list of protic and aprotic solvents, their dielectric constants, boiling points, and melting points is given in Table 8-5. This table will be useful in selecting solvents for nucleophilic substitution reactions.
With regard to \(\text{S}_\text{N}2\) reactions, the solvent can affect profoundly the reactivity of a given nucleophile. Thus anions such as \(Cl^\ominus\) and \(CN^\ominus\), which are weakly nucleophilic in hydroxylic solvents and in poor ionizing solvents such as 2-propanone (acetone), become very significantly nucleophilic in polar aprotic sovlents such as \(\left( CH_3 \right)_2 SO\). The reason is that for salts such as \(NaCl\) and \(NaCN\) the aprotic solvent preferentially solvates the cation, leaving the anion relatively bare. This dissociation of the anion from the cation together with its poor solvation makes the anion abnormally reactive as a nucleophile.
\(^6\)The Greek letters \(\alpha\), \(\beta\), \(\gamma\) are used here not as nomenclature, but to designated the positions along a carbon chain from a functional group, \(X\): \(C_\omega \cdots C_\delta-C_\gamma-C_\beta-C_\alpha-X\) (also see Section 7-10).
\(^7\)Specifically, electrostatic force \(= q_1 q_2/r_{12}^2 \epsilon\) in which \(q_1\) and \(q_2\) are the charges, \(r_{12}\) is the distance between the charges, and \(\epsilon\) is the dielectric constant of the medium; \(\epsilon = 1\) for a vacuum.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


