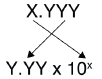14.9: The pH and pOH Scales - Ways to Express Acidity and Basicity
- Page ID
- 47568
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Define pH and pOH.
- Determine the pH of acidic and basic solutions.
- Determine the hydronium ion concentration and pOH from pH.
As we have seen, \([H_3O^+]\) and \([OH^−]\) values can be markedly different from one aqueous solution to another. So chemists defined a new scale that succinctly indicates the concentrations of either of these two ions.
\(pH\) is a logarithmic function of \([H_3O^+]\):
\[pH = −\log[H_3O^+] \label{pH} \]
\(pH\) is usually (but not always) between 0 and 14. Knowing the dependence of \(pH\) on \([H_3O^+]\), we can summarize as follows:
- If pH < 7, then the solution is acidic.
- If pH = 7, then the solution is neutral.
- If pH > 7, then the solution is basic.
This is known as the \(pH\) scale. The pH scale is the range of values from 0 to 14 that describes the acidity or basicity of a solution. You can use \(pH\) to make a quick determination whether a given aqueous solution is acidic, basic, or neutral. Figure \(\PageIndex{1}\) illustrates this relationship, along with some examples of various solutions. Because hydrogen ion concentrations are generally less than one (for example \(1.3 \times 10^{-3}\,M\)), the log of the number will be a negative number. To make pH even easier to work with, pH is defined as the negative log of \([H_3O^+]\), which will give a positive value for pH.
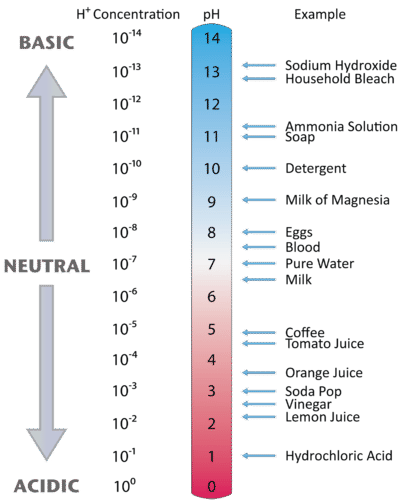
Label each solution as acidic, basic, or neutral based only on the stated \(pH\).
- milk of magnesia, pH = 10.5
- pure water, pH = 7
- wine, pH = 3.0
Answer
- With a pH greater than 7, milk of magnesia is basic. (Milk of magnesia is largely Mg(OH)2.)
- Pure water, with a pH of 7, is neutral.
- With a pH of less than 7, wine is acidic.
Identify each substance as acidic, basic, or neutral based only on the stated \(pH\).
- human blood with \(pH\) = 7.4
- household ammonia with \(pH\) = 11.0
- cherries with \(pH\) = 3.6
- Answer a
- basic
- Answer b
- basic
- Answer c
- acidic
Calculating pH from Hydronium Concentration
The pH of solutions can be determined by using logarithms as illustrated in the next example for stomach acid. Stomach acid is a solution of \(HCl\) with a hydronium ion concentration of \(1.2 \times 10^{−3}\; M\), what is the \(pH\) of the solution?
\[ \begin{align} \mathrm{pH} &= \mathrm{-\log [H_3O^+]} \nonumber \\ &=-\log(1.2 \times 10^{−3}) \nonumber \\ &=−(−2.92)=2.92 \nonumber \end{align} \nonumber \]
To get the log value on your calculator, enter the number (in this case, the hydronium ion concentration) first, then press the LOG key.
If the number is 1.0 x 10-5 (for [H3O+] = 1.0 x 10-5 M) you should get an answer of "-5".
If you get a different answer, or an error, try pressing the LOG key before you enter the number.
Find the pH, given the \([H_3O^+]\) of the following:
- 1 ×10-3 M
- 2.5 ×10-11 M
- 4.7 ×10-9 M
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given:
Find: ? pH |
| Plan the problem. |
Need to use the expression for pH (Equation \ref{pH}). pH = - log [H3O+] |
| Calculate. |
Now substitute the known quantity into the equation and solve.
The other issue that concerns us here is significant figures. Because the number(s) before the decimal point in a logarithm relate to the power on 10, the number of digits after the decimal point is what determines the number of significant figures in the final answer:
|
Find the pH, given [H3O+] of the following:
- 5.8 ×10-4 M
- 1.0×10-7
- Answer a
- 3.22
- Answer b
- 7.00
Calculating Hydronium Concentration from pH
Sometimes you need to work "backwards"—you know the pH of a solution and need to find \([H_3O^+]\), or even the concentration of the acid solution. How do you do that? To convert pH into \([H_3O^+]\) we solve Equation \ref{pH} for \([H_3O^+]\). This involves taking the antilog (or inverse log) of the negative value of pH .
\[[\ce{H3O^{+}}] = \text{antilog} (-pH) \nonumber \]
or
\[[\ce{H_3O^+}] = 10^{-pH} \label{ph1} \]
As mentioned above, different calculators work slightly differently—make sure you can do the following calculations using your calculator.
We have a solution with a pH = 8.3. What is [H3O+] ?
With some calculators you will do things in the following order:
- Enter 8.3 as a negative number (use the key with both the +/- signs, not the subtraction key).
- Use your calculator's 2nd or Shift or INV (inverse) key to type in the symbol found above the LOG key. The shifted function should be 10x.
- You should get the answer 5.0 × 10-9.
Other calculators require you to enter keys in the order they appear in the equation.
- Use the Shift or second function to key in the 10x function.
- Use the +/- key to type in a negative number, then type in 8.3.
- You should get the answer 5.0 × 10-9.
If neither of these methods work, try rearranging the order in which you type in the keys. Don't give up—you must master your calculator!
Find the hydronium ion concentration in a solution with a pH of 12.6. Is this solution an acid or a base? How do you know?
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: pH = 12.6 Find: [H3O+] = ? M |
| Plan the problem. |
Need to use the expression for [H3O+] (Equation \ref{ph1}). [H3O+] = antilog (-pH) or [H3O+] = 10-pH |
| Calculate. |
Now substitute the known quantity into the equation and solve. [H3O+] = antilog (12.60) = 2.5 x 10-13 M (2 significant figures since 4.7 has 12.60 2 decimal places) or [H3O+] = 10-12.60 = 2.5 x 10-13 M (2 significant figures since 4.7 has 12.60 2 decimal places) The other issue that concerns us here is significant figures. Because the number(s) before the decimal point in a logarithm relate to the power on 10, the number of digits after the decimal point is what determines the number of significant figures in the final answer:
|
If moist soil has a pH of 7.84, what is [H3O+] of the soil solution?
- Answer
- 1.5 x 10-8 M
The pOH scale
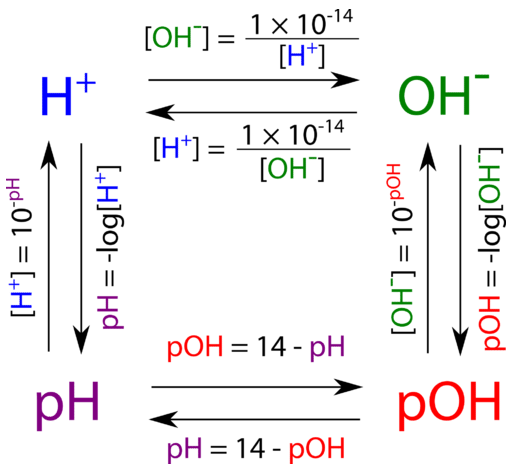
As with the hydrogen-ion concentration, the concentration of the hydroxide ion can be expressed logarithmically by the pOH. The pOH of a solution is the negative logarithm of the hydroxide-ion concentration.
\[\text{pOH} = -\text{log} \left[ \ce{OH^-} \right] \nonumber \]
The relation between the hydronium and hydroxide ion concentrations expressed as p-functions is easily derived from the \(K_w\) expression:
\[K_\ce{w}=\ce{[H_3O^+][OH^- ]} \label{\(\PageIndex{6}\)} \]
\[-\log K_\ce{w}=\mathrm{-\log([H_3O^+][OH^−])=-\log[H_3O^+] + -\log[OH^-]}\label{\(\PageIndex{7}\)} \]
\[\mathrm{p\mathit{K}_w=pH + pOH} \label{\(\PageIndex{8}\)} \]
At 25 °C, the value of \(K_w\) is \(1.0 \times 10^{−14}\), and so:
\[\mathrm{14.00=pH + pOH} \label{\(\PageIndex{9}\)} \]
The hydronium ion molarity in pure water (or any neutral solution) is \( 1.0 \times 10^{-7}\; M\) at 25 °C. The pH and pOH of a neutral solution at this temperature are therefore:
\[\mathrm{pH=-\log[H_3O^+]=-\log(1.0\times 10^{−7}) = 7.00} \label{\(\PageIndex{1}\)0} \]
\[\mathrm{pOH=-\log[OH^−]=-\log(1.0\times 10^{−7}) = 7.00} \label{\(\PageIndex{1}\)1} \]
And so, at this temperature, acidic solutions are those with hydronium ion molarities greater than \( 1.0 \times 10^{-7}\; M\) and hydroxide ion molarities less than \( 1.0 \times 10^{-7}\; M\) (corresponding to pH values less than 7.00 and pOH values greater than 7.00). Basic solutions are those with hydronium ion molarities less than \( 1.0 \times 10^{-7}\; M\) and hydroxide ion molarities greater than \( 1.0 \times 10^{-7}\; M\) (corresponding to pH values greater than 7.00 and pOH values less than 7.00).
Find the pOH of a solution with a pH of 4.42.
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: pH =4.42 Find: ? pOH |
| Plan the problem. |
Need to use the expression pOH = 14 - pH |
| Calculate. |
Now substitute the known quantity into the equation and solve. pOH=14−4.42=9.58 |
| Think about your result. | The pH is that of an acidic solution, and the resulting pOH is the difference after subtracting from 14. The answer has two significant figures because the given pH has two decimal places. |
The pH of a solution is 8.22. What is the pOH?
- Answer
- 5.78
The diagram below shows all of the interrelationships between [H3O+][H3O+], [OH−][OH−], pH, and pOH.
Contributions & Attributions
Peggy Lawson (Oxbow Prairie Heights School). Funded by Saskatchewan Educational Technology Consortium.
- Template:OpenStax