14.8: Water - Acid and Base in One
- Page ID
- 47566
- Describe the autoionization of water.
- Calculate the concentrations of \(\ce{H3O^{+}}\) and \(\ce{OH^{−}}\) in aqueous solutions, knowing the other concentration.
We have already seen that \(\ce{H2O}\) can act as an acid or a base:
\[\color{blue}{\underbrace{\ce{NH3}}_{\text{base}}} + \color{red}{\underbrace{\ce{H2O}}_{\text{acid}}} \color{black} \ce{<=> NH4^{+} + OH^{−}} \nonumber \]
where \(\ce{H2O}\) acts as an \(\color{red}{\text{acid}}\) (in red).
\[\color{red}{\underbrace{\ce{HCl}}_{\text{acid}}} + \color{blue}{\underbrace{\ce{H2O}}_{\text{base}}} \color{black} \ce{-> H3O^{+} + Cl^{−}} \nonumber \]
where \(\ce{H2O}\) acts as an \(\color{blue}{\text{base}}\) (in blue).
It may not surprise you to learn, then, that within any given sample of water, some \(\ce{H2O}\) molecules are acting as acids, and other \(\ce{H2O}\) molecules are acting as bases. The chemical equation is as follows:
\[\color{red}{\underbrace{\ce{H2O}}_{\text{acid}}} + \color{blue}{\underbrace{\ce{H2O}}_{\text{base}}} \color{black} \ce{<=> H3O^{+} + OH^{−}} \label{Auto} \]
This occurs only to a very small degree: only about 6 in 108 \(\ce{H2O}\) molecules are participating in this process, which is called the autoionization of water.
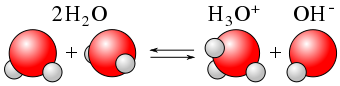
At this level, the concentration of both \(\ce{H3O^{+}(aq)}\) and \(\ce{OH^{−}(aq)}\) in a sample of pure \(\ce{H2O}\) is about \(1.0 \times 10^{−7}\, M\) (at room temperature). If we use square brackets—[ ]—around a dissolved species to imply the molar concentration of that species, we have
\[\color{red}{\ce{[H3O^{+}]}} \color{black}{ = } \color{blue}{\ce{[OH^{-}]}} \color{black} = 1.0 \times 10^{-7} \label{eq5} \]
for any sample of pure water because H2O can act as both an acid and a base. The product of these two concentrations is \(1.0\times 10^{−14}\):
\[\color{red}{\ce{[H3O^{+}]}} \color{black}{\times} \color{blue}{\ce{[OH^{-}]}} \color{black} = (1.0 \times 10^{-7})( 1.0 \times 10^{-7}) = 1.0 \times 10^{-14} \nonumber \]
- For acids, the concentration of \(\ce{H3O^{+}(aq)}\) (i.e., \(\ce{[H3O^{+}]}\)) is greater than \(1.0 \times 10^{−7}\, M\).
- For bases the concentration of \(\ce{OH^{−}(aq)}\) (i.e., \(\ce{[OH^{−}]}\)) is greater than \(1.0 \times 10^{−7}\, M\).
However, the product of the two concentrations—\(\ce{[H3O^{+}][OH^{−}]}\)—is always equal to \(1.0 \times 10^{−14}\), no matter whether the aqueous solution is an acid, a base, or neutral:
\[\color{red}{\ce{[H_3O^+]}} \color{blue}{\ce{[OH^{-}]}} \color{black} = 1.0 \times 10^{-14} \nonumber \]
This value of the product of concentrations is so important for aqueous solutions that it is called the autoionization constant of water and is denoted \(K_w\):
\[K_w = \color{red}{\ce{[H_3O^+]}} \color{blue}{\ce{[OH^{-}]}} \color{black} = 1.0 \times 10^{-14} \label{eq10} \]
This means that if you know \(\ce{[H3O^{+}]}\) for a solution, you can calculate what \(\ce{[OH^{−}]}\)) has to be for the product to equal \(1.0 \times 10^{−14}\); or if you know \(\ce{[OH^{−}]}\)), you can calculate \(\ce{[H3O^{+}]}\). This also implies that as one concentration goes up, the other must go down to compensate so that their product always equals the value of \(K_w\).
The degree of autoionization of water (Equation \ref{Auto})—and hence the value of \(K_w\)—changes with temperature, so Equations \ref{eq5} - \ref{eq10} are accurate only at room temperature.
What is \(\ce{[OH^{−}]}\)) of an aqueous solution if \(\ce{[H3O^{+}]}\) is \(1.0 \times 10^{−4} M\)?
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: \(\ce{[H3O^{+}]} =1.0 \times 10^{−4}\, M\) Find: [OH−] = ? M |
| List other known quantities. | none |
| Plan the problem. |
Using the expression for \(K_w\), (Equation \ref{eq10}), rearrange the equation algebraically to solve for [OH−]. \[\left [ \ce{OH^{-}} \right ]=\dfrac{1.0\times 10^{-14}}{\left [ H_3O^+ \right ]} \nonumber \] |
| Calculate. |
Now substitute the known quantities into the equation and solve. \[\left [\ce{ OH^{-}} \right ]=\dfrac{1.0\times 10^{-14}}{1.0\times 10^{-4}}=1.0\times 10^{-10}M\nonumber \] It is assumed that the concentration unit is molarity, so \(\ce{[OH^{−}]}\) is 1.0 × 10−10 M. |
| Think about your result. | The concentration of the acid is high (> 1 x 10-7 M), so \(\ce{[OH^{−}]}\) should be low. |
What is \(\ce{[OH^{−}]}\) in a 0.00032 M solution of H2SO4?
- Hint
-
Assume both protons ionize from the molecule...although this is not the case.
- Answer
- \(3.1 \times 10^{−11}\, M\)
When you have a solution of a particular acid or base, you need to look at the formula of the acid or base to determine the number of H3O+ or OH− ions in the formula unit because \(\ce{[H_3O^{+}]}\) or \(\ce{[OH^{−}]}\)) may not be the same as the concentration of the acid or base itself.
What is \(\ce{[H_3O^{+}]}\) in a 0.0044 M solution of \(\ce{Ca(OH)_2}\)?
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: \([\ce{Ca(OH)_2}] =0.0044 \,M\) Find: \(\ce{[H_3O^{+}]}\) = ? M |
| List other known quantities. |
We begin by determining \(\ce{[OH^{−}]}\). The concentration of the solute is 0.0044 M, but because \(\ce{Ca(OH)_2}\) is a strong base, there are two OH− ions in solution for every formula unit dissolved, so the actual \(\ce{[OH^{−}]}\) is two times this: \[\ce{[OH^{−}] = 2 \times 0.0044\, M = 0.0088 \,M.} \nonumber \] |
| Plan the problem. |
Use the expression for \(K_w\) (Equation \ref{eq10}) and rearrange the equation algebraically to solve for \(\ce{[H_3O^{+}]}\). \[\left [ H_3O^{+} \right ]=\dfrac{1.0\times 10^{-14}}{\left [ OH^{-} \right ]} \nonumber \] |
| Calculate. |
Now substitute the known quantities into the equation and solve. \[\left [ H_3O^{+} \right ]=\dfrac{1.0\times 10^{-14}}{(0.0088)}=1.1\times 10^{-12}M \nonumber \] \(\ce{[H_3O^{+}]}\) has decreased significantly in this basic solution. |
| Think about your result. | The concentration of the base is high (> 1 x 10-7 M) so \(\ce{[H_3O^+}]}\) should be low. |
What is \(\ce{[H_3O^{+}]}\) of an aqueous solution if \(\ce{[OH^{−}]}\) is \(1.0 \times 10^{−9}\, M\)?
- Answer
- 1.0 × 10−5 M
In any aqueous solution, the product of \(\ce{[H_3O^{+}]}\) and \(\ce{[OH^{−}]}\) equals \(1.0 \times 10^{−14}\) (at room temperature).

