9.4: The Bohr Model - Atoms with Orbits
- Page ID
- 47516
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Define an energy level in terms of the Bohr model.
- Discuss how the Bohr model can be used to explain atomic spectra.
Electric light bulbs contain a very thin wire in them that emits light when heated. The wire is called a filament. The particular wire used in light bulbs is made of tungsten. A wire made of any metal would emit light under these circumstances, but tungsten was chosen because the light it emits contains virtually every frequency and therefore, the light emitted by tungsten appears white. A wire made of some other element would emit light of some color that was not convenient for our uses. Every element emits light when energized by heating or passing electric current through it. Elements in solid form begin to glow when they are heated sufficiently, and elements in gaseous form emit light when electricity passes through them. This is the source of light emitted by neon signs and is also the source of light in a fire.

Each Element Has a Unique Spectrum
The light frequencies emitted by atoms are mixed together by our eyes so that we see a blended color. Several physicists, including Angstrom in 1868 and Balmer in 1875, passed the light from energized atoms through glass prisms in such a way that the light was spread out so they could see the individual frequencies that made up the light. The emission spectrum (or atomic spectrum) of a chemical element is the unique pattern of light obtained when the element is subjected to heat or electricity.

When hydrogen gas is placed into a tube and electric current passed through it, the color of emitted light is pink. But when the color is spread out, we see that the hydrogen spectrum is composed of four individual frequencies. The pink color of the tube is the result of our eyes blending the four colors. Every atom has its own characteristic spectrum; no two atomic spectra are alike. The image below shows the emission spectrum of iron. Because each element has a unique emission spectrum, elements can be defined using them.

You may have heard or read about scientists discussing what elements are present in the sun or some more distant star, and after hearing that, wondered how scientists could know what elements were present in a place no one has ever been. Scientists determine what elements are present in distant stars by analyzing the light that comes from stars and finding the atomic spectrum of elements in that light. If the exact four lines that compose hydrogen's atomic spectrum are present in the light emitted from the star, that element contains hydrogen.
Bohr's Model of the Atom
By 1913, the concept of the atom had evolved from Dalton's indivisible spheres idea, to J. J. Thomson's plum pudding model, and then to Rutherford's nuclear atom theory. Rutherford, in addition to carrying out the brilliant experiment that demonstrated the presence of the atomic nucleus, also proposed that the electrons circled the nucleus in a planetary type motion. The solar system or planetary model of the atom was attractive to scientists because it was similar to something with which they were already familiar, namely the solar system.

Unfortunately, there was a serious flaw in the planetary model. It was already known that when a charged particle (such as an electron) moves in a curved path, it gives off some form of light and loses energy in doing so. This is, after all, how we produce TV signals. If the electron circling the nucleus in an atom loses energy, it would necessarily have to move closer to the nucleus as it loses energy, and would eventually crash into the nucleus. Furthermore, Rutherford's model was unable to describe how electrons give off light forming each element's unique atomic spectrum. These difficulties cast a shadow on the planetary model and indicated that, eventually, it would have to be replaced.
In 1913, the Danish physicist Niels Bohr proposed a model of the electron cloud of an atom in which electrons orbit the nucleus and were able to produce atomic spectra. Understanding Bohr's model requires some knowledge of electromagnetic radiation (or light).
Energy Levels
Bohr's key idea in his model of the atom is that electrons occupy definite orbitals that require the electron to have a specific amount of energy. In order for an electron to be in the electron cloud of an atom, it must be in one of the allowable orbitals and it must have the precise energy required for that orbit. Orbits closer to the nucleus would require smaller amounts of energy for an electron, and orbits farther from the nucleus would require the electron to have a greater amount of energy. The possible orbits are known as energy levels. One of the weaknesses of Bohr's model was that he could not offer a reason why only certain energy levels or orbits were allowed.
Bohr hypothesized that the only way electrons could gain or lose energy would be to move from one energy level to another, thus gaining or losing precise amounts of energy. The energy levels are quantized, meaning that only specific amounts are possible. It would be like a ladder that had rungs only at certain heights. The only way you can be on that ladder is to be on one of the rungs, and the only way you could move up or down would be to move to one of the other rungs. Suppose we had such a ladder with 10 rungs. Other rules for the ladder are that only one person can be on a rung in the normal state, and the ladder occupants must be on the lowest rung available. If the ladder had five people on it, they would be on the lowest five rungs. In this situation, no person could move down because all of the lower rungs are full. Bohr worked out rules for the maximum number of electrons that could be in each energy level in his model, and required that an atom in its normal state (ground state) had all electrons in the lowest energy levels available. Under these circumstances, no electron could lose energy because no electron could move down to a lower energy level. In this way, Bohr's model explained why electrons circling the nucleus did not emit energy and spiral into the nucleus.
Bohr's Model and Atomic Spectra
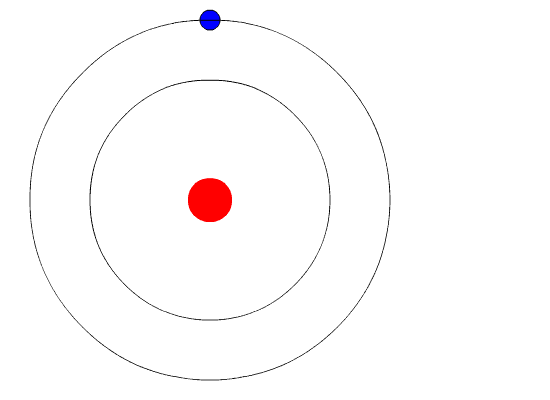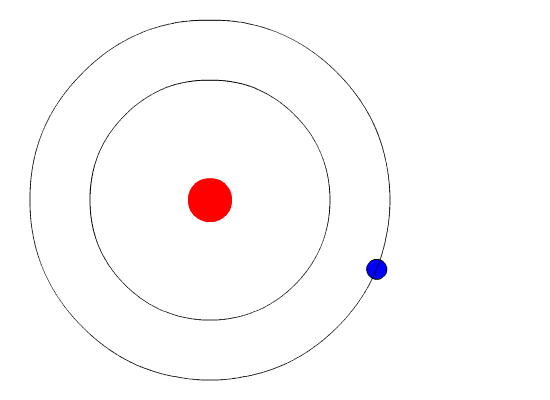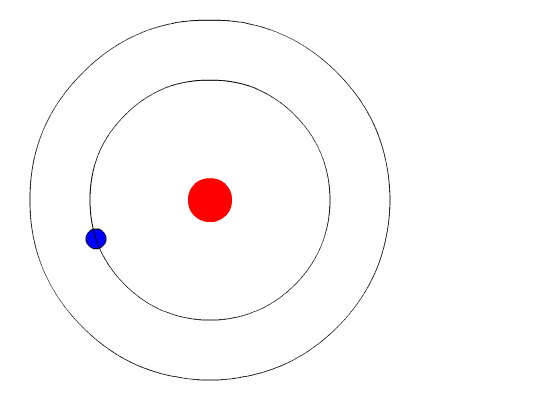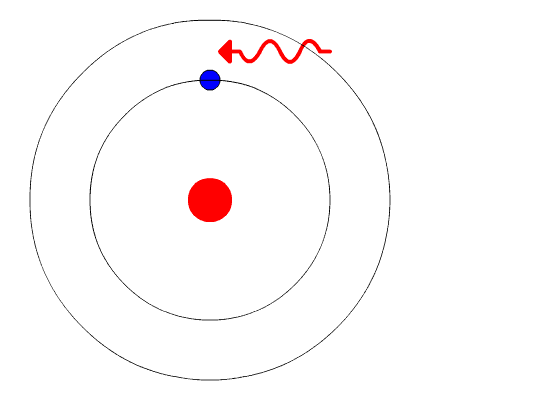
The evidence used to support Bohr's model came from the atomic spectra. He suggested that an atomic spectrum is made by the electrons in an atom moving energy levels. The electrons typically have the lowest energy possible, called the ground state. If the electrons are given energy (through heat, electricity, light, etc.) the electrons in an atom could absorb energy by jumping to a higher energy level, or excited state. The electrons then give off the energy in the form of a piece of light—called a photon—that they had absorbed, to fall back to a lower energy level. The energy emitted by electrons dropping back to lower energy levels will always be precise amounts of energy, because the differences in energy levels are precise. This explains why you see specific lines of light when looking at an atomic spectrum—each line of light matches a specific "step down" that an electron can take in that atom. This also explains why each element produces a different atomic spectrum. Because each element has different acceptable energy levels for its electrons, the possible steps each element's electrons can take differ from all other elements.
Summary
- Bohr's model suggests each atom has a set of unchangeable energy levels, and electrons in the electron cloud of that atom must be in one of those energy levels.
- Bohr's model suggests that the atomic spectra of atoms is produced by electrons gaining energy from some source, jumping up to a higher energy level, then immediately dropping back to a lower energy level and emitting the energy difference between the two energy levels.
- The existence of the atomic spectra is support for Bohr's model of the atom.
- Bohr's model was only successful in calculating energy levels for the hydrogen atom.
Vocabulary
- Emission spectrum (or atomic spectrum) - The unique pattern of light given off by an element when it is given energy.
- Energy levels - Possible orbits that an electron can have in the electron cloud of an atom.
- Ground state - To be in the lowest energy level possible.
- Excited state - To be in a higher energy level.
- Photon - A piece of electromagnetic radiation, or light, with a specific amount of energy.
- Quantized - To have a specific amount.

