3.2: Confirmations

Learning Objectives

• Draw sawhorse projections and Newman projections of simple organic compounds.
• Name, predict relative stability, and energy barriers to interconversion of conformations of simple organic compounds, including ethane, butane, and cyclohexane.
• Draw chair conformations of cyclohexane, substituted cyclohexanes, and their flipped forms, and predict the stability of the bulky groups at the axial and equatorial positions.

Representing orientation of groups connected to a \(\ce{C-C}\) bond

There are multiple ways of visualizing the orientation of atoms along a \(\ce{C-C}\) bond, including sawhorse projection, Newman projection, and Fisher projection.

Sawhorse projection and Newman projection of a molecule

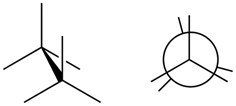
• Sawhorse projection looks at the \(\ce{C-C}\) bond from an oblique angle, as shown in Figure \(\PageIndex{1}\).
• Newman projection looks from front to back with the front atom represented as a dot with bonds originating from the dot and the back atom is represented as a wheel with bonds shown as lines originating from the wheel, as illustrated in Figure \(\PageIndex{1}\).

Model showing viewpoints by arrows

Sawhorse projection

Newman projection

Figure \(\PageIndex{1}\): Model with the viewpoints indicated by arrows, sawhorse projection, and Newman projection of butane (\(\ce{CH3CH2CH2CH3}\). (Copyright; Public domain)

The relative orientation of groups connected to the two \(\ce{C's}\) of \(\ce{C-C}\) bond is quantitatively shown by the dihedral angle.

Dihedral angle or torsion angel

Dihedral angle or torsion angle is the clockwise angle between half-planes through two sets of three atoms, e.g., the half-planes defined by \(\ce{R-C-C}\) and \(\ce{R'-C-C}\) in Figure \(\PageIndex{2}\), having two atoms in common \(\ce{C-C}\) in this case).

Figure \(\PageIndex{2}\): Dihedral angle \(\alpha\) between the half-planes defined by \(\ce{R-C-C}\) and\( \ce{R'-C-C}\) in a hydrocarbon \(\ce{RCH2CH2R'}\) molecule (Copyright; Д.Ильин: vectorization, Public domain via Wikimedia commons)

Conformational isomers

The torsion angle changes due to free rotation around the single bond. However, the rotation is not completely free; there are energy barriers. Therefore, as the torsion angle gradually changes from 0^o to 360^o, the relative potential energy of the molecule goes through local minima to local maxima, often at intervals of 60^o.

Conformations

• Conformations are the different arrangements of atoms in a molecule resulting from rotation around a single bond.
  • Eclipsed conformation is a conformation in which two substituents on adjacent atoms are at 0^o torsion angle and the
  • Staggered conformation is the confirmation in which the two substituents on adjacent atoms are at 60^o torsion angle, as illustrated in Figure \(\PageIndex{3}\).

Eclipsed conformation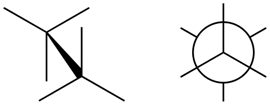

Staggered conformation

Figure \(\PageIndex{3}\): Eclipsed conformation in sawhorse projection (left) and Newman projection (right) and the corresponding staggered conformation (Copyright; Jovianeye, Public domain via Wikimedia commons).

Conformations of ethane

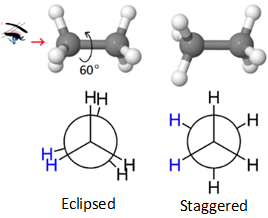The eclipsed and staggered conformations of ethane are shown in the figure on the right. The eclipsed conformation of ethane is higher energy (unstable) relative to staggered confirmation by 12.5 kJ/mol. The eclipsed conformation changes to staggered, and vice versa, after every 60^o rotation around the \(\ce{C-C}\) bond as illustrated in Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\): Newman projections of ethane conformations for rotation around C-C bond & their relative energy differences (not total energies) vs. torsional/dihedral angle curve, where the conformation A is staggered, and B is eclipsed. (Copyright; Keministi, Public domain via Wikimedia commons)

Factors in stabilizing or destabilizing conformations

Factors that contribute to the stabilization or destabilization of the conformation are the following.

1. Destabilization due to electrostatic repulsion between the same charge dipoles in close proximity in eclipsed conformation,
2. destabilization due to steric repulsion, i.e., physical repulsion of the groups due to space requirement in close proximity in eclipsed conformation, and
3. stabilization due to hyperconjugation, i.e., an overlap of a \(\sigma\)-bond on one atom with an antibonding orbital on the neighboring atom in staggered conformation.

These factors are illustrated in Figure \(\PageIndex{5}\) for the case of ethane.

Figure \(\PageIndex{5}\): Illustrates the contributions of steric and electrostatic interactions as well as hyperconjugation to the energy barrier of rotation in ethane (Copyright; UMMedChemStudent, CC BY-SA 3.0, via Wikimedia Commons)

Conformations of butane

The most stable conformation of butane (\(\ce{CH3CH2CH2CH3}\)) for a view of C2-C3 bond is illustrated on the right. This staggered conformation with the bulky (\(\ce{-CH3}\) groups in this case) fathers apart is given a special name,'anti' and labeled A in the relative energy vs. tortion angle curve shown in Figure \(\PageIndex{6}\).

Figure \(\PageIndex{6}\): Newman projections of butane conformations for rotation around C2-C3 bond and their relative energy differences (not total energies) vs. torsional/dihedral angle curve. A: antiperiplanar, anti or trans, B: gauche, C: eclipsed, D: synperiplanar or cis. (Copyright; aKeministi, Public domain via Wikimedia commons)

A 60^o rotation converts the anti-conformation to eclipsed conformation, labeled C in the figure, which is 16 kJ/mol higher energy relative to the anti-confirmation. A further 60^o rotation converts the eclipsed conformation to another staggered conformation called gauche-conformation, labeled B, at a local energy minimum but 3.8 kJ/mol higher than anti-conformation. The gauche-conformation has the bulky (\(\ce{-CH3}\) in this case) groups at 60^o torsion angle where they are close enough to cause some steric repulsion between each other. Another 60^o rotation converts the gauche-conformation to an eclipsed conformation called cis, labeled D, in which the bulky (\(\ce{-CH3}\) in this case) groups are eclipsing each other. This cis-conformation is 3 kJ/mol higher in energy than the other eclipsed confirmation (labeled B) and it is the highest energy conformation of butane. These conformations keep repeating at an interval of 60^o torsion angle as illustrated in Figure \(\PageIndex{6}\).

Conformational isomers

• Conformations corresponding to local minima on the potential energy curve, e.g., anti- and gauche-conformations in the case of butane, are called conformational isomers, conformers, or rotamers.
• The conformations corresponding to the local maxima on the energy curve, e.g., eclipsed conformations in the case of butane, are the transition states between the conformational isomers.

Energy cost of eclipsing and gauche interaction of \(\ce{-H}\) and \(\ce{-CH3}\) groups

It can be calculated form Figure \(\PageIndex{4}\) and Figure \(\PageIndex{6}\) that each

• \(\ce{-H}\) to \(\ce{-H}\) eclipsing costs 4 kJ/mol,
• \(\ce{-H}\) to \(\ce{-CH3}\) eclipsing costs 6 kJ/mol,
• \(\ce{-CH3}\) to \(\ce{-CH3}\) eclipsing costs 11 kJ/mol, and
• \(\ce{-CH3}\) to \(\ce{-CH3}\) gauche interaction costs 3.8 kJ/mol.

Conformations and strains in cycloalkanes

If a cycloalkane is in a planar conformation, i.e., all the \(\ce{C's}\) in the chain be in the same plane, there will be two kinds of strain:

1. angle strain, i.e., the strain caused by bending the bond angles from the ideal tetrahedal bond angles of 109.5^o, and
2. eclipsing strains between a pair of \(\ce{H}\) on each \(\ce{C}\) with pairs of \(\ce{H's}\) on the two neighboring carbons.

Cyclopropane has a planar ring with bond angles reduced to 60^o and three pairs of eclipsing \(\ce{H's}\), resulting in an overall ring strain of ~120 kJ/mol.

A planar cyclobutane would have bond angles reduced to 90^o and four pairs of eclipsing \(\ce{H's}\), but it changes to a puckered confirmation that increases angle strain a little but significantly reduces the eclipsing strain, resulting in an overall ring strain ~110 kJ/mol.

A planar cyclopentane would have bond angles of 108^o, i.e., close to the regular value of 109.5^o, but five pairs of eclipsing \(\ce{H's}\). Cyclopentane is puckered, increasing angle strain slightly but significantly reducing the eclipsing strain, resulting in an overall strain of ~25 kJ/mol. Four of the \(\ce{C's}\) of cyclopentane are almost in one plane and the fifth is raised, giving it an envelope shape, also called envelop conformation. Cyclopentane is one of the most common ring structures found in nature due to its low angle strain. For example, ribose -a sugar that is a component of DNA monomers, and fructose or fruit sugar are five-membered rings.

Cyclohexane acquires a bent conformation that looks like a chair -called chair conformation, in which all bond angles are close to the tetrahedral value of 109.5^o and all \(\ce{H's}\) are staggered with no ring strain. Cyclohexane is the most common ring structure due to its zero ring strain. For example, glucose -the most common monosaccharide (sugar) is six-membered rings. Starch, a carbohydrate component of food, and cellulose, a major component of wood, are made of glucose units. The conformations of cyclopropane, cyclobutane, cyclopentane, and cyclohexane are illustrated below.

Cyclopropane, Ring strain ~120 kJ/mol

Cyclobutane Ring strain ~110 kJ/mol

Cyclopentane Ring strain ~25 kJ/mol

Cyclohexane No ring strain

Medium-size rings (7-13 \(\ce{C's}\)) can pucker/bend to minimize angle strain but some transannular strain, i.e., steric repulsion between groups attached to non-adjacent ring atoms, appear between groups on some \(\ce{C's}\) with other groups at a distance across the ring. For example, the figure on the right highlights the transannular strain between some \(\ce{H's}\) with a red triangle in the lowest energy conformation of cyclodecane (Copyright; Chem540f09grp4, Public domain, via Wikimedia Commons). In larger rings (14 or more \(\ce{C's}\)), there is little or no ring strain. The order of strain in cyclic hydrocarbons is the following: cyclopropane > cyclobutane > cyclopentane > cyclohexane < cycloheptane <cyclooctane.

Conformations of cyclohexane

Cyclohexane which is the most common cyclic structure, exists primarily in a chair conformation in which all bonds are 111^o, i.e., very close to tetrahedral value 109.5^o, and all six pairs of \(\ce{H's}\) are staggered as shown in Figure \(\PageIndex{7}\).

Model of chair conformation

Edge-on view of chair conformation

Newman projection

Figure \(\PageIndex{7}\): Cyclohexane: a model of chair conformation, edge-on view, and Newman projection from the left side of the edge-one view showing staggered conformation. (Copyright; model: public domain, edge-one view: Roland.chem, Public domain, via Wikimedia Commons, and Newman projection: Chem Sim 2001, Public domain, via Wikimedia Commons)

Drawing chair conformation of cyclohexane

Follow the following 5 steps to draw the chair form of a cyclohexane ring.

1. Draw two parallel lines slanting down, separated by about half their length, and the bottom line starting from about the middle of the first as shown in Figure \(\PageIndex{8}\).
2. Start a line from the lower end of the bottom line making a wide V shape, and extend it to about parallel to the top of the top line. Draw a line parallel to the first one in this step, starting from the top of the top line and extending to about the bottom of the bottom line. Figure \(\PageIndex{8}\) shows these two lines in blue.
3. Connect the top of the right side line of step 2 to the bottom end of the top line of step 1 and do the same to the other line of step 2. These are shown in red in Figure \(\PageIndex{8}\). The chair skeleton of the cyclohexane ring is complete at this stage.
4. Draw lines starting from the corners of the ring, going upwards from the corners pointing up, and going downwards from the corners pointing down. These bonds are approximately parallel to the axis of the ring called axial bonds, shown in green in Figure \(\PageIndex{8}\).
5. Draw lines starting from the corners making a big V-shape to the axial bond and approximately parallel to the bond one bond away in the ring. These are approximately along the equator of the ring and called equatorial bonds, shown in black, blue, and red, corresponding to the color of the bonds one bond away to which they are drawn parallel in Figure \(\PageIndex{8}\).

Figure \(\PageIndex{8}\): Illustration of steps to draw chair conformation of cyclohexane (right) and its flipped form (right). (Copyrights; Public domain)

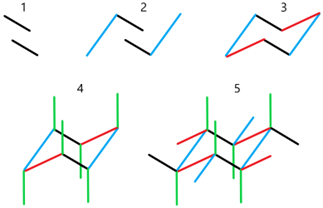
There are two chair conformations. They are flipped form of each other. To draw the flipped form of the first, follow the same five steps but start with two parallel lines slanting upwards, as illustrated in Figure \(\PageIndex{8}\).

Ring flipping in cyclohexane

There is limited rotation around \(\ce{C-C}\) in a cyclohexane chain that allows flipping of the cyclohexane ring that converts all the axial bonds into equatorial and all the equatorial bonds to axial as illustrated by animation and drawing in Figure \(\PageIndex{9}\).

Figure \(\PageIndex{9}\): Animation of cyclohexane ring flipping (left) and sketch showing all axial bonds become equatorial and voice versa upon flipping the ring. (Copyrights; animation: Cleanthis, Public domain, via Wikimedia Commons, and the sketch: Naturwiki, Public domain, via Wikimedia Commons)

The ring flipping goes through twist boat conformation and half-chair and boat transition states with higher energy conformations as shown in Figure \(\PageIndex{10}\). The two chair conformations are of equal energy in the case of cyclohexane and predominant in the mixture due to their low energy. For every 10,000 molecules in chair conformations, there is no more than one molecule in the twist boat conformation.

Figure \(\PageIndex{10}\):Cyclohexane chair flip (ring inversion) reaction plotted against their energy differences. Inversion happens quickly & constantly at room temperature. A1 & A2: chair; B1 & B2: twist-boat; C: boat; and D1 & D2: half-chair. (Copyright; Keministi, Public domain via Wikimedia commons)

Conformations of monosubstituted cyclohexanes

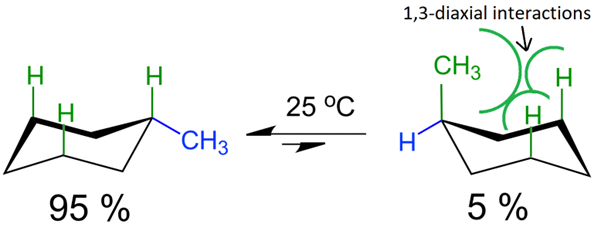
Two chair conformations of cyclohexane are of equal energy. When one of the \(\ce{H}\) is replaced with a bulky group like \(\ce{-CH3}\) group, the bulky group is at an equatorial position in one and at an axial position in the other chair conformation and the two are not the same energy. The bulky group at the axial position has steric repulsion with the other two axial \(\ce{H's}\) on the same face of the ring, called 1,3-diaxial interaction, as illustrated in Fig. 11. Therefore, the chair conformation with the bulky group at equatorial position is more stable and more predominant at equilibrium than its flipped form with the bulky group at axial position. This effect depends on the size of the group; the larger the group the stronger the effect.

Figure \(\PageIndex{11}\): Illustration of the equilibrium between axial and equatorial methylcyclohexanes with an illustration of the destabilizing steric repulsion in the axial methylcyclohexane, sketch (left) and model (right) with the steric strain area highlighted by circles and indicated by arrows. (Copyright; Public domain)

Preference of equatorial groups over axial groups in nature

Six-membered rings are the most common. Among them, those with all or most of the bulky groups in equatorial positions are significantly more common because of the stability of the equatorial relative to the axial bulky groups. For example, several six-membered ring monosaccharides (sugars) have the most bulky groups in equatorial positions. Glucose with all the bulky groups at the equatorial positions is the most common among them. Glucose units combine through an equatorial group to form a polymer called cellulose, the major component of wood. Starch is also a polymer of glucose but with one connecting bond axial. This changing connecting bond from equatorial to axial changes cellulose, a hard structural material, to starch, a carbohydrate. Wood can survive centuries, but starch would get rotten and decompose in a few days if left out in the open. The structures of glucose, starch, and cellulose are shown in Figure \(\PageIndex{12}\).

Glucose

Starch

Cellulose

Figure \(\PageIndex{12}\): Structure of glucose, starch, and cellulose. (Copyright; glucose: Yikrazuul, Public domain, via Wikimedia Commons, Starch, and cellulose: NEUROtiker, Public domain, via Wikimedia Commons)

Fused ring systems also exist in nature; most have six- and five-membered rings. For example, the basic skeleton of steroid hormones is three six-membered rings designated A, B, and C, and one five-membered ring designated D, fused, as shown in Fig 13. The \(\ce{C-C}\) bond shared between the two fused rings is the bridge. The two \(\ce{C's}\) at the ends of the bridge are bridgehead \(\ce{C's}\). Each bridgehead \(\ce{C}\) has two \(\ce{C-C}\) bonds, one in each of the fused rings. Trans ring fusion has all four bonds, from the bridgehead \(\ce{C's}\) into the two fused rings, equatorial and cis ring fusion has one of the four bonds axial. Steroid hormones always have trans-fused rings B, C, and D, as shown in Fig. 13. Ring A may be cis-fused, as in example 5\(\beta\) in Figure \(\PageIndex{1}\), but in a majority of cases, it is also trans-fused as in example 5\(\alpha\) in Figure \(\PageIndex{1}\). This is because the cis fusion with one axial \(\ce{C-C}\) bond at the ring connection is associated with steric strain.

Figure \(\PageIndex{1}\): Steroid 5\(\alpha\) and 5\(\beta\) stereoisomers. (Copyright; Leprof 7272, CC BY-SA 3.0, via Wikimedia Commons)