4.7: Stoichiometric calculations

Conversion factors from a chemical equation

Stoichiometry pronounced as “stɔɪkiˈɒmɪtri” is the calculation of the amount of reactants and products in a chemical reaction. It is based on the fact that a balanced chemical equation is also a set of mole-to-mole equalities between the reactants and the products. Each equality gives two conversion factors that allow calculating the mole of one substance from the given mole of any other substance in the equation.

Fig. 4.6.1 lists the chemical equation for photosynthesis reaction, the mole-to-mole equalities from the equation, and the two conversion factors from each of the equality, as an example. The conversion factors are used to calculate the unknown quantity in the mole from the known quantity in the mole of any other reactant or product in the same chemical equation, as explained in the following examples.

Figure \(\PageIndex{1}\): Balanced chemical equation of the photosynthesis reaction, mol-to-mol equalities, and conversion factors derived from the equation.

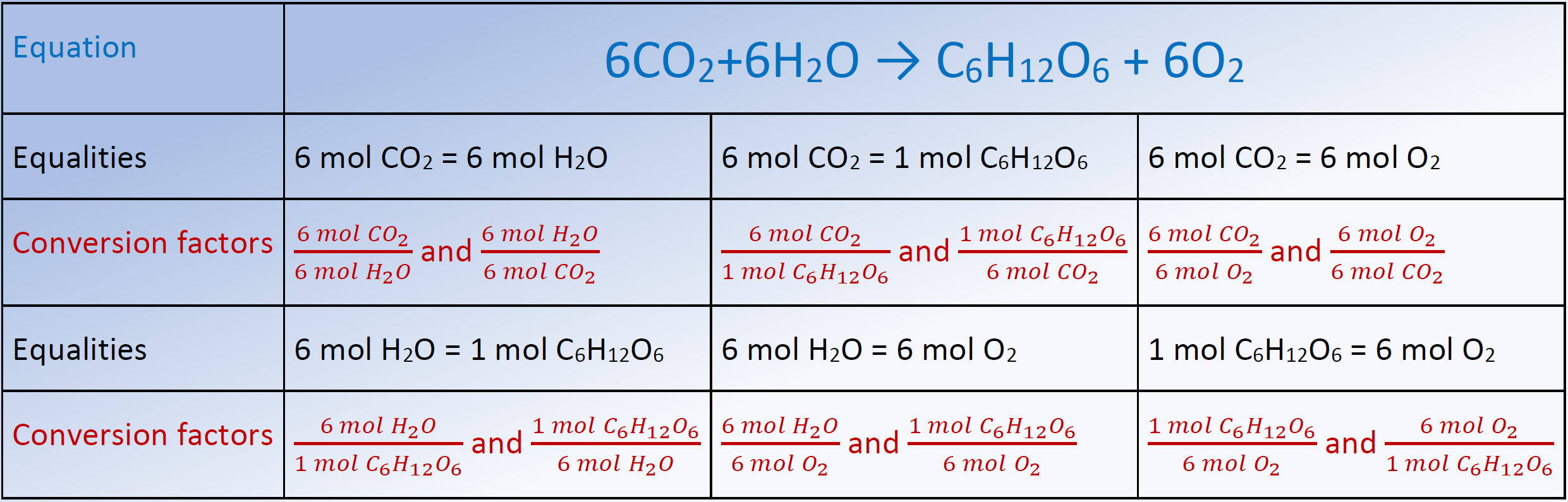
Mole-to-mole conversion from a chemical equation

Calculation of the mole of the desired substance from the given mole of any reactant or product needs one conversion factor. The steps are:

1. write the given quantity and the desired quantity,
2. write the balanced chemical equation,
3. write the equality between the given and the desired substances,
4. right the conversion factor that has the given substance in the denominator and the desired substance in the numerator,
5. multiply the given quantity with the conversion factor. Double-check to make sure that it cancels the given substance and leaves the desired substance in the answer.

Example \(\PageIndex{1}\)

Calculate the moles of glucose produced from 3.0 moles of carbon dioxide in the photosynthesis reaction?

Solution

i. Given: 3.0 mole CO₂, Desired: ? moles of C₆H₁₂O₆

ii. Chemical equation: \(\ce{6CO2 + 6H2O -> C6H12O6 + 6O2}\)

iii. The desired equality: 6 mol CO₂ = 1 mol C₆H₁₂O₆,

iv. Desired conversion factor: \(\frac{1 \mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}{6 \mathrm{~mol} \mathrm{~CO_2}}\)

v. Calculations:\[3.0 \cancel{\mathrm {~mol~CO_2}} \times \frac{1 \mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}{6 \cancel{\mathrm{~mol} \mathrm{~CO_2}}}=0.50 \mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}\nonumber\]

Example \(\PageIndex{2}\)

Magnesium reacts with HCl by this reaction: \(\ce{Mg(s) + 2HCl(aq) -> MgCl2(aq) + H2(g)^}\). Calculate the moles of Mg needed to produce 3 moles of H₂?

Solution

i. Given: 3 mol of H₂. Desired: ? Moles of Mg.

ii. The chemical equation is given.

iii. The desired equality: 1 mol Mg = 1 mol H₂.

iv. The desired conversion factor: \(\frac{1 ~mol~Mg}{1 ~mol{~H}_{2}}\)

v. Calculation: \[3 \cancel{\mathrm{~mol} \mathrm{~H}_{2}} \times \frac{1 \mathrm{~mol} \mathrm{~Mg}}{1 \cancel{\mathrm{~mol} \mathrm{~H}_{2}}}=3 \operatorname{~mol} ~M g\nonumber\]

Mole-to-mass conversion from a chemical equation

Calculations described in the previous two examples show calculating moles of the desired substance from the moles of the given substance using a conversion factor from a chemical equation. The molar mass is a conversion factor from a mole-to-gram of the substance. So, add a molar mass of the desired substance as a second conversion factor, as explained in the following examples. Double-check that all the units cancel out, leaving the mass unit of the desired substance in the final answer.

Example \(\PageIndex{3}\)

Calculate grams of AgCl precipitate formed from 2.0 moles of CaCl₂ consumed in the following reaction: \[\ce{2AgNO3 + CaCl2 -> Ca(NO3)2 + 2AgCl(s)(v)}\nonumber\]

Solution

i. Given: 2.0 moles of CaCl₂. Desired: ? g AgCl

ii. Molar mass of AgCl = 1x107.87 g Ag.mol^-1 + 1x35.45 g C.mol^-1 = 143.3 g AgCl.mol^-1

iii. The chemical equation is given.

iv. The desired equality: 1 mol CaCl₂ = 2 mol AgCl, and 1 mol AgCl =143.3 g AgCl.

v. The desired conversion factors: \[\frac{2 \mathrm{~mol} \mathrm{~AgCl}}{1 \mathrm{~mol} \mathrm{~CaCl}_{2}} \quad\text { and }\quad \frac{143.3 \mathrm{~g} \mathrm{~AgCl}}{1 \mathrm{~mol} \mathrm{~AgCl}}\nonumber\]

vi. Calculation: \[2.0\cancel{\mathrm{~mol}\mathrm{~CaCl}_{2}}\times\frac{2 \cancel{\mathrm{~mol} \mathrm{~AgCl}}}{1 \cancel{\mathrm{~mol} \mathrm{~CaCl}_{2}}} \times\frac{143.3 \mathrm{~g} \mathrm{~AgCl}}{1 \cancel{\mathrm{~mol} \mathrm{~AgCl}}}=573.3 \mathrm{~g} \mathrm{~AgCl}\nonumber\]

Example \(\PageIndex{4}\)

How many grams of carbon dioxide are needed to react with 2 moles of water in the photosynthesis reaction?

Solution

i. Given: 2.0 moles of H₂O Desired: ? g CO₂.

ii. Molar mass of CO₂ = 1x12.011 g C.mol^-1 + 2x15.999 g O.mol^-1 = 44.009 g CO₂.mol^-1

iii. The chemical equation: : 6CO₂ + 6 H₂O → C₆H₁₂O₆ + 6O₂.

iv. The desired equality: 6 mol CO₂ = 6 mol H₂O, and 1 mol CO₂ = = 44.009 g CO₂.

v. The desired conversion factors: \[\frac{6 \mathrm{~mol} \mathrm{~CO}_{2}}{6 \mathrm{~mol} \mathrm{~H}_{2}}\mathrm{O}\quad \text { and }\quad \frac{44.009 \mathrm{~g} \mathrm{~CO}_{2}}{1 \mathrm{~mol} \mathrm{~CO}_{2}}\nonumber\]

vi. Calculation: \[2.0 \cancel{\mathrm{~mol} \mathrm{~} \mathrm{H}_{2} \mathrm{O}} \times \frac{6 \cancel{\mathrm{~mol} \mathrm{~CO}_{2}}}{6 \cancel{\mathrm{~mol} \mathrm{~H}_{2} \mathrm{O}}} \times \frac{44.009 \mathrm{~g} \mathrm{~CO}_{2}}{1 \cancel{\mathrm{~mol} \mathrm{~CO}_{2}}}=88 \mathrm{~g} \mathrm{~CO}{ }_{2}\nonumber\]

Mass-to-mass conversion from a chemical equation

A chemical equation gives a mole-to-mole conversion factor. If the given substance is in grams and the desired substance is also in grams, then two additional conversion factors based on the molar masses are needed. That is, the following conversions are needed:

Mass of given substance⇒mole of the given substance⇒mole of the desired substance⇒grams of the desired substance.

The reciprocal molar mass of the given substance is the first conversion factor, the mole to mole conversion factor from the chemical equation is the second conversion factor, and the molar mass of the desired substance is the third conversion factor needed. Make sure that each conversion factor cancels the denominator unit of its multiplier to the right, and the desired unit is left in the answer. The following examples explain these calculations.

Example \(\PageIndex{5}\)

How many grams of Mg are needed to produce 1.01 g of H₂ gas in this reaction: \[\ce{Mg(s) + 2HCl(aq) -> MgCl2(aq) + H2(g)^}\nonumber\]

Solution

i. Given: 1.01 g H₂ Desired: ? g Mg.

ii. Molar mass of H₂ = 2 x1.008 g H.mol^-1 = 2.016 g H₂.mol^-1, and molar mass = 24.305 g Mg.mol^-1.

iii. The chemical equation is given in the problem.

iv. The desired equalities : 1 mol Mg = 1 mol H₂, 1 mol H₂ = 2.016g H₂, 1 mol Mg = 24.305 g Mg

v. Calculate by multiplying the given quantity consecutively with the three desired conversion factors from the equalities:

\[1.01 \cancel{\mathrm{~g ~H_{2}}} \times \frac{1 \cancel{\mathrm{~mol} \mathrm{~H}_{2}}}{2.016 \cancel{\mathrm{~g} \mathrm{~H}_{2}}} \times \frac{1 \cancel{\mathrm{~mol} \mathrm{~Mg}}}{1 \cancel{\mathrm{~mol} \mathrm{~H}_{2}}} \times \frac{24.305 \mathrm{~g} \mathrm{~Mg}}{1 \cancel{\mathrm{~mol} \mathrm{~Mg}}}=11.9 \mathrm{~g~Mg}\nonumber\]

Example \(\PageIndex{6}\)

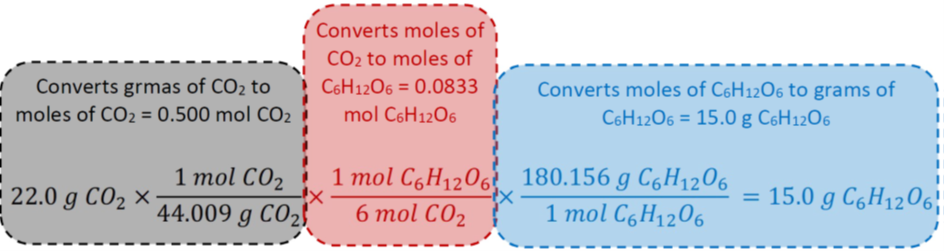
How many grams of glucose are produced if 22.0 g of carbon dioxide is consumed in the photosynthesis reaction?

Solution

i. Given: 22.0 g CO₂ Desired: ? g C₆H₁₂O₆.

ii. Molar masses: of CO₂ = 1x12.011 g C.mol^-1 + 2x15.999 g O.mol^-1 = 44.009 g CO₂.mol^-1, and molar mass of C₆H₁₂O₆ = 6x12.011 g C.mol^-1 + 12x1.008 g H.mol^-1 + 6x15.999 g O.mol^-1 = 180.156 g C₆H₁₂O₆.mol^-1 .

iii. The chemical equation: \(\ce{6CO2 + 6H2O -> C6H12O6 + 6O2}\)

iv. The desired equalities: 6 mol CO₂ = 1 mol C₆H₁₂O₆, 1 mol CO₂ = 44.009 g CO₂, 1 mol C₆H₁₂O₆ = 180.156 g C₆H₁₂O₆.

v. Calculate by multiplying the given quantity consecutively with the three desired conversion factors from the equalities:

\[22.0 \cancel{\mathrm{~g} \mathrm{~CO}_{2}} \times \frac{1 \cancel{\mathrm{~mol} \mathrm{~CO}_{2}}}{44.009 \cancel{\mathrm{~g} \mathrm{~CO}_{2}}} \times \frac{1 \cancel{\mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}}{6 \cancel{\mathrm{~mol} \mathrm{~CO}_{2}}} \times \frac{180.156 \mathrm{~g} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}{1 \cancel{\mathrm{~mol} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}}}=15.0 \mathrm{~g} \mathrm{~C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}\nonumber\]

Fig. 4.6.2 illustrates what each conversion factor does in the case of the above example number 4.6.5

Figure \(\PageIndex{2}\): Illustration of the operation of conversion factors in a mass-to-mass calculation based on a balanced chemical equation of example 4..6.6 for question: "calculate grams of C₆H₁₂O₆ produced from 22.0 g CO₂ in photosynthesis reaction \(\ce{6CO2 + 6H2O -> C6H12O6 + 6O2}\)”.