6.4: Mole-Mole Relationships in Chemical Reactions
- Page ID
- 16114
- To use a balanced chemical reaction to determine molar relationships between the substances.
Previously, you learned to balance chemical equations by comparing the numbers of each type of atom in the reactants and products. The coefficients in front of the chemical formulas represent the numbers of molecules or formula units (depending on the type of substance). Here, we will extend the meaning of the coefficients in a chemical equation.
Consider the simple chemical equation
\[\ce{2H_2 + O_2 → 2H_2O}\nonumber \]
The convention for writing balanced chemical equations is to use the lowest whole-number ratio for the coefficients. However, the equation is balanced as long as the coefficients are in a 2:1:2 ratio. For example, this equation is also balanced if we write it as
\[\ce{4H_2 + 2O_2 → 4H_2O}\nonumber \]
The ratio of the coefficients is 4:2:4, which reduces to 2:1:2. The equation is also balanced if we were to write it as
\[\ce{22H_2 + 11O_2 → 22H_2O}\nonumber \]
because 22:11:22 also reduces to 2:1:2.
Suppose we want to use larger numbers. Consider the following coefficients:
\[12.044 \times 10^{23}\; H_2 + 6.022 \times 10^{23}\; O_2 → 12.044 \times 10^{23}\; H_2O\nonumber \]
These coefficients also have the ratio 2:1:2 (check it and see), so this equation is balanced. But 6.022 × 1023 is 1 mol, while 12.044 × 1023 is 2 mol (and the number is written that way to make this more obvious), so we can simplify this version of the equation by writing it as
\[\ce{2 \;mol\; H_2 + 1\; mol\; O_2 → 2 \;mol\; H_2O}\nonumber \]
We can leave out the word mol and not write the 1 coefficient (as is our habit), so the final form of the equation, still balanced, is
\[\ce{2H_2 + O_2 → 2H_2O}\nonumber \]
Now we interpret the coefficients as referring to molar amounts, not individual molecules. The lesson? Balanced chemical equations are balanced not only at the molecular level but also in terms of molar amounts of reactants and products. Thus, we can read this reaction as “two moles of hydrogen react with one mole of oxygen to produce two moles of water.”
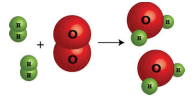
2 molecules H2 1 molecule O2 2 molecules H2O
2 moles H2 1 mole O2 2 moles H2O
2 x 2.02 g=4.04 g H2 32.0 g O2 2 x 18.02 g=36.04 g H2O
Figure \(\PageIndex{1}\): This representation of the production of water from oxygen and hydrogen show several ways to interpret the quantitative information of a chemical reaction.
By the same token, the ratios we constructed to describe molecules reaction can also be constructed in terms of moles rather than molecules. For the reaction in which hydrogen and oxygen combine to make water, for example, we can construct the following ratios:
\[\mathrm{\dfrac{2\: mol\: H_2}{1\: mol\: O_2}\: or\: \dfrac{1\: mol\: O_2}{2\: mol\: H_2}}\nonumber \]
\[\mathrm{\dfrac{2\: mol\: H_2O}{1\: mol\: O_2}\: or\: \dfrac{1\: mol\: O_2}{2\: mol\: H_2O}}\nonumber \]
\[\mathrm{\dfrac{2\: mol\: H_2}{2\: mol\: H_2O}\: or\: \dfrac{2\: mol\: H_2O}{2\: mol\: H_2}}\nonumber \]
We can use these ratios to determine what amount of a substance, in moles, will react with or produce a given number of moles of a different substance. The study of the numerical relationships between the reactants and the products in balanced chemical reactions is called stoichiometry. The ratio of coefficients in a balanced chemical equation, used in computations relating amounts of reactants and products is called the stoichiometric factor.
How many moles of oxygen react with hydrogen to produce 27.6 mol of H2O? The balanced equation is as follows:
\[\ce{2H2 + O2 -> 2H2O} \nonumber \nonumber \]
Solution
Because we are dealing with quantities of H2O and O2, we will use the stoichiometric ratio that relates those two substances. Because we are given an amount of H2O and want to determine an amount of O2, we will use the ratio that has H2O in the denominator (so it cancels) and O2 in the numerator (so it is introduced in the answer). Thus,
\(\mathrm{27.6\: mol\: H_2O\times\dfrac{1\: mol\: O_2}{2\: mol\: H_2O}=13.8\: mol\: O_2}\)
To produce 27.6 mol of H2O, 13.8 mol of O2 react.
Using 2H2 + O2 → 2H2O, how many moles of hydrogen react with 3.07 mol of oxygen to produce H2O?
- Answer
-
\(\mathrm{3.07\: mol\: O_2\times\dfrac{2\: mol\: H_2}{1\: mol\: O_2}=6.14\: mol\: H_2}\)
Key Takeaway
- The balanced chemical reaction can be used to determine molar relationships between substances.


