6.5: Mole-Mass and Mass-Mass Problems
- Page ID
- 16116
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To convert from mass or moles of one substance to mass or moles of another substance in a chemical reaction.
We have established that a balanced chemical equation is balanced in terms of moles as well as atoms or molecules. We have used balanced equations to set up ratios, now in terms of moles of materials, that we can use as conversion factors to answer stoichiometric questions, such as how many moles of substance A react with so many moles of reactant B. We can extend this technique even further. Recall that we can relate a molar amount to a mass amount using molar mass. We can use that ability to answer stoichiometry questions in terms of the masses of a particular substance, in addition to moles. We do this using the following sequence:
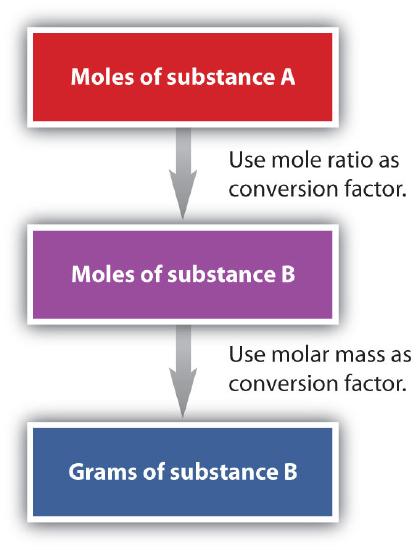
Collectively, these conversions are called mole-mass calculations.
As an example, consider the balanced chemical equation
\[\ce{Fe_2O_3 + 3SO_3 \rightarrow Fe_2(SO_4)_3} \nonumber \nonumber \]
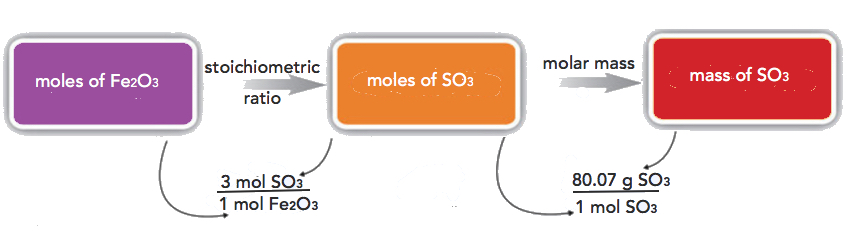
If we have 3.59 mol of Fe2O3, how many grams of SO3 can react with it? Using the mole-mass calculation sequence, we can determine the required mass of SO3 in two steps. First, we construct the appropriate molar ratio, determined from the balanced chemical equation, to calculate the number of moles of SO3 needed. Then using the molar mass of SO3 as a conversion factor, we determine the mass that this number of moles of SO3 has.
The first step resembles the exercises we did in Section 6.4. As usual, we start with the quantity we were given:
\[\mathrm{3.59\: mol\: Fe_2O_3\times\dfrac{3\: mol\: SO_3}{1\: mol\: Fe_2O_3}=10.77\: mol\: SO_3} \nonumber \nonumber \]
The mol Fe2O3 units cancel, leaving mol SO3 unit. Now, we take this answer and convert it to grams of SO3, using the molar mass of SO3 as the conversion factor:
\[\mathrm{10.77\: mol\: SO_3\times\dfrac{80.07\: g\: SO_3}{1\: mol\: SO_3}=862.4\: g\: SO_3} \nonumber \nonumber \]
Our final answer is expressed to three significant figures. Thus, in a two-step process, we find that 862 g of SO3 will react with 3.59 mol of Fe2O3. Many problems of this type can be answered in this manner.
The same two-step problem can also be worked out in a single line, rather than as two separate steps, as follows:
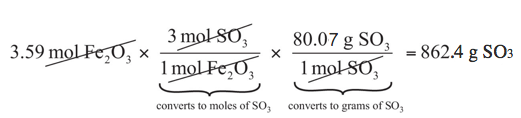
We get exactly the same answer when combining all the math steps together as we do when we calculate one step at a time.
How many grams of CO2 are produced if 2.09 mol of HCl are reacted according to this balanced chemical equation?
\[\ce{CaCO_3 + 2HCl \rightarrow CaCl_2 + CO_2 + H_2O} \nonumber \]
Solution
Our strategy will be to convert from moles of HCl to moles of CO2 and then from moles of CO2 to grams of CO2. We will need the molar mass of CO2, which is 44.01 g/mol. Performing these two conversions in a single-line gives 46.0 g of CO2:
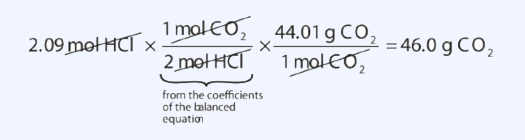
The molar ratio between CO2 and HCl comes from the balanced chemical equation.
How many grams of glucose (C6H12O6) are produced if 17.3 mol of H2O are reacted according to this balanced chemical equation?
\[\ce{6CO_2 + 6H_2O \rightarrow C_6H_{12}O_6 + 6O_2} \nonumber \]
- Answer
-
\(\mathrm{17.3\: mol\: H_2O\times\dfrac{1\: mol\: C_6H_{12}O_6}{6\: mol\: H_2O}\times\dfrac{180.18\: g\: C_6H_{12}O_6}{1\: mol\: C_6H_{12}O_6}=520\: g\: C_6H_{12}O_6}\)
It is a small step from mole-mass calculations to mass-mass calculations. If we start with a known mass of one substance in a chemical reaction (instead of a known number of moles), we can calculate the corresponding masses of other substances in the reaction. The first step in this case is to convert the known mass into moles, using the substance’s molar mass as the conversion factor. Then—and only then—we use the balanced chemical equation to construct a conversion factor to convert that quantity to moles of another substance, which in turn can be converted to a corresponding mass. Sequentially, the process is as follows:
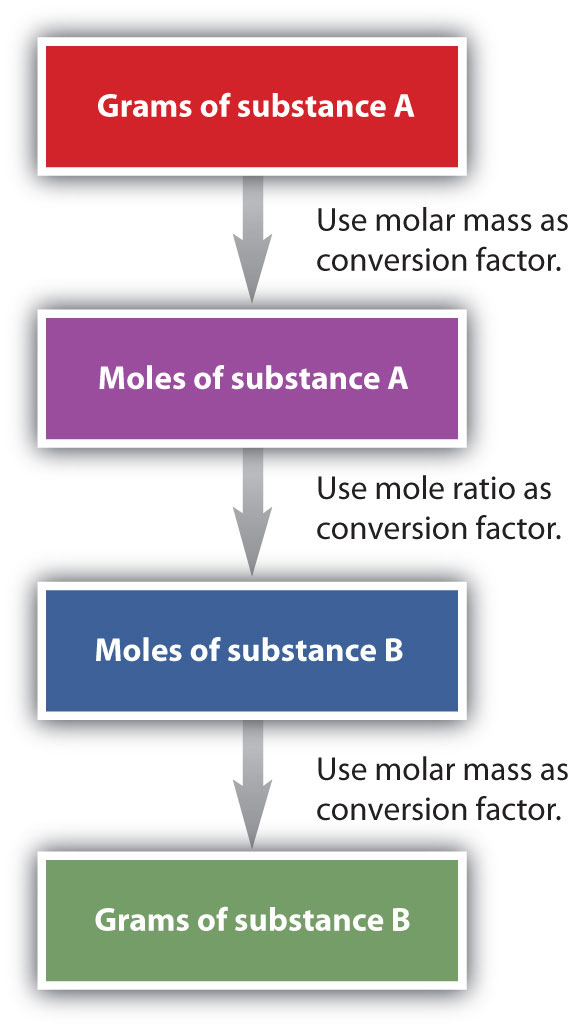
This three-part process can be carried out in three discrete steps or combined into a single calculation that contains three conversion factors. The following example illustrates both techniques.
Methane can react with elemental chlorine to make carbon tetrachloride (\(\ce{CCl4}\)). The balanced chemical equation is as follows:
\[\ce{CH_4 + 4Cl_2 \rightarrow CCl_4 + 4HCl} \nonumber \]
How many grams of HCl are produced by the reaction of 100.0 g of \(\ce{CH4}\)?
Solution
First, let us work the problem in stepwise fashion. We begin by converting the mass of \(\ce{CH4}\) to moles of \(\ce{CH4}\), using the molar mass of \(\ce{CH4}\) (16.05 g/mol) as the conversion factor:
\(\mathrm{100.0\: g\: CH_4\times\dfrac{1\: mol\: CH_4}{16.05\: g\: CH_4}=6.231\: mol\: CH_4}\)
Note that we inverted the molar mass so that the gram units cancel, giving us an answer in moles. Next, we use the balanced chemical equation to determine the ratio of moles \(\ce{CCl4}\) and moles HCl and convert our first result into moles of HCl:
\(\mathrm{6.231\: mol\: CH_4\times\dfrac{4\: mol\: HCl}{1\: mol\: CH_4}=24.92\: mol\: HCl}\)
Finally, we use the molar mass of HCl (36.46 g/mol) as a conversion factor to calculate the mass of 24.92 mol of HCl:
\(\mathrm{24.92\: mol\: HCl\times\dfrac{36.46\: g\: HCl}{1\: mol\: HCl}=908.5\: g\: HCl}\)
In each step, we have limited the answer to the proper number of significant figures. If desired, we can do all three conversions on a single line:

\(\mathrm{100.0\: g\: CH_4\times\dfrac{1\: mol\: CH_4}{16.05\: g\: CH_4}\times\dfrac{4\: mol\: HCl}{1\: mol\: CH_4}\times\dfrac{36.46\: g\: HCl}{1\: mol\: HCl}=908.7\: g\: HCl}\)
This final answer is slightly different from our first answer because only the final answer is restricted to the proper number of significant figures. In the first answer, we limited each intermediate quantity to the proper number of significant figures. As you can see, both answers are essentially the same.
The oxidation of propanal (CH3CH2CHO) to propionic acid (CH3CH2COOH) has the following chemical equation:
CH3CH2CHO + 2K2Cr2O7 → CH3CH2COOH + other products
How many grams of propionic acid are produced by the reaction of 135.8 g of K2Cr2O7?
- Answer
-
\(\mathrm{135.8\: g\: K_2Cr_2O_7\times\dfrac{1\: mol\: K_2Cr_2O_7}{294.20\: g\: K_2Cr_2O_7}\times\dfrac{1\: mol\: CH_3CH_2COOH}{2\: mol\: K_2Cr_2O_7}\times\dfrac{74.09\: g\: CH_3CH_2COOH}{1\: mol\: CH_3CH_2COOH}=17.10\: g\: CH_3CH_2COOH}\)
Taxol is a powerful anticancer drug that was originally extracted from the Pacific yew tree (Taxus brevifolia). As you can see from the accompanying figure, taxol is a very complicated molecule, with a molecular formula of \(\ce{C47H51NO14}\). Isolating taxol from its natural source presents certain challenges, mainly that the Pacific yew is a slow-growing tree, and the equivalent of six trees must be harvested to provide enough taxol to treat a single patient. Although related species of yew trees also produce taxol in small amounts, there is significant interest in synthesizing this complex molecule in the laboratory.
After a 20-year effort, two research groups announced the complete laboratory synthesis of taxol in 1994. However, each synthesis required over 30 separate chemical reactions, with an overall efficiency of less than 0.05%. To put this in perspective, to obtain a single 300 mg dose of taxol, you would have to begin with 600 g of starting material. To treat the 26,000 women who are diagnosed with ovarian cancer each year with one dose, almost 16,000 kg (over 17 tons) of starting material must be converted to taxol. Taxol is also used to treat breast cancer, with which 200,000 women in the United States are diagnosed every year. This only increases the amount of starting material needed.
Clearly, there is intense interest in increasing the overall efficiency of the taxol synthesis. An improved synthesis not only will be easier but also will produce less waste materials, which will allow more people to take advantage of this potentially life-saving drug.
Key Takeaway
- A balanced chemical equation can be used to relate masses or moles of different substances in a reaction.


