Periodic Trends in Ionic Radii
- Page ID
- 619
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An understanding of periodic trends is necessary when analyzing and predicting molecular properties and interactions. Common periodic trends include those in ionization energy, atomic radius, and electron affinity. One such trend is closely linked to atomic radii -- ionic radii. Neutral atoms tend to increase in size down a group and decrease across a period. When a neutral atom gains or loses an electron, creating an anion or cation, the atom's radius increases or decreases, respectively. This module explains how this occurs and how this trend differs from that of atomic radii.
Shielding and Penetration
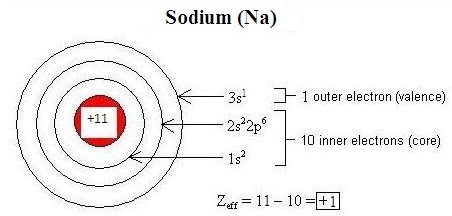
Electromagnetic interactions between electrons in an atom modify the effective nuclear charge (\(Z_{eff}\)) on each electron. Penetration refers to the presence of an electron inside the shell of an inner electron, and shielding is the process by which an inner electron masks an outer electron from the full attractive force of the nucleus, decreasing \(Z_{eff}\). Differences in orbital characteristics dictate differences in shielding and penetration. Within the same energy level (indicated by the principle quantum number, n), due to their relative proximity to the nucleus, s-orbital electrons both penetrate and shield more effectively than p-orbital electrons, and p electrons penetrate and shield more effectively than d-orbital electrons. Shielding and penetration along with the effective nuclear charge determine the size of an ion. An overly-simplistic but useful conceptualization of effective nuclear charge is given by the following equation:
\[Z_{eff} = Z - S \nonumber \]
where
- \(Z\) is the number of protons in the nucleus of an atom or ion (the atomic number), and
- \(S\) is the number of core electrons.
Figure \(\PageIndex{1}\) illustrates how this equation can be used to estimate the effective nuclear charge of sodium:
Cations and Anions
Neutral atoms that have lost an electron exhibit a positive charge and are called cations. These cations are smaller than their respective atoms; this is because when an electron is lost, electron-electron repulsion (and therefore, shielding) decreases and the protons are better able to pull the remaining electrons towards the nucleus (in other words, \(Z_{eff}\)increases). A second lost electron further reduces the radius of the ion. For instance, the ionic radius of Fe2+ is 76 pm, while that of Fe3+ is 65 pm. If creation of an ion involves completely emptying an outer shell, then the decrease in radius is especially great.
Neutral atoms that have gained an electron are called anions, and they are much larger than their respective atoms. As an additional electron occupies an outer orbital, there is increased electron-electron repulsion (and hence, increased shielding) which pushes the electrons further apart. Because the electrons now outnumber the protons in the ion, the protons can not pull the extra electrons as tightly toward the nucleus; this results in decreased \(Z_{eff}\).
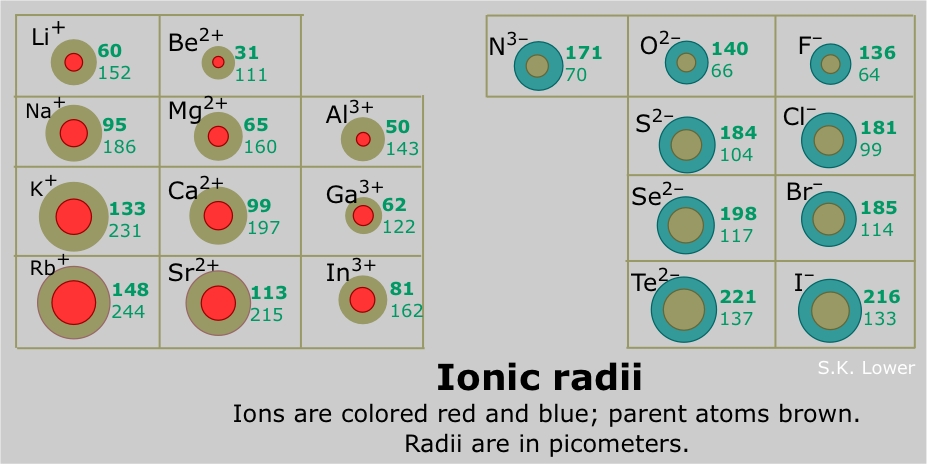
Figure 2 shows an isoelectric series of atoms and ions (each has the same number of electrons, and thus the same degree of electron-electron repulsion and shielding) with differing numbers of protons (and thus different nuclear attraction), giving the relative ionic sizes of each atom or ion.
The Periodic Trend
Due to each atom’s unique ability to lose or gain an electron, periodic trends in ionic radii are not as ubiquitous as trends in atomic radii across the periodic table. Therefore, trends must be isolated to specific groups and considered for either cations or anions.
Consider the s- and d-block elements. All metals can lose electrons and form cations. The alkali and alkali earth metals (groups 1 and 2) form cations which increase in size down each group; atomic radii behave the same way. Beginning in the d-block of the periodic table, the ionic radii of the cations do not significantly change across a period. However, the ionic radii do slightly decrease until group 12, after which the trend continues (Shannon 1976). It is important to note that metals, not including groups 1 and 2, can have different ionic states, or oxidation states, (e.g. Fe2+ or Fe3+ for iron) so caution must be employed when generalizing about trends in ionic radii across the periodic table.
All non-metals (except for the noble gases which do not form ions) form anions which become larger down a group. For non-metals, a subtle trend of decreasing ionic radii is found across a pegroup theoryriod (Shannon 1976). Anions are almost always larger than cations, although there are some exceptions (i.e. fluorides of some alkali metals).
Measurement and Factors Affecting Ionic Radii
The ionic radius of an atom is measured by calculating its spatial proportions in an ionic bond with another ion within a crystal lattice. However, it is to consistently and accurately determine the proportions of the ionic bonds. After comparing many compounds, chemist Linus Pauling assign a radius of 140 pm to O2- and use this as a reference point to determine the sizes of other Ionic Radii (Jensen 2010).
Ionic radius is not a permanent trait of an ion, but changes depending on coordination number, spin state, and other variables (Shannon 1976). For a given ion, the ionic radius increases with increasing coordination number and is larger in a high-spin state than in a low-spin state.
According to group theory, the idea of ionic radii as a measurement of spherical shapes only applies to ions that form highly-symmetric crystal lattices like Na+ and Cl -. The point group symmetry of a lattice determines whether or not the ionic radii in that lattice can be accurately measured (Johnson 1973). For instance, lattices with Oh and Td symmetries are considered to have high symmetry; thus the electron densities of the component ions occupy relatively-spherical regions and ionic radii can be measured fairly accurately. However, for less symmetrical and more polar lattices such as those with Cn, Cnh, and Cnv symmetries, significant changes in the electron density can occur, causing deviations from spherical shape; these deviations make ionic radii more difficult to measure.
References
- Housecroft, Catherine E. & Alan G. Sharpe. Inorganic Chemistry. 3rd ed. England: Pearson Education Limited, 2008.
- Shannon R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallographica 1976;32(5): 751-767.
- Jensen B., William. The Origin of the Ionic-Radius Ratio Rules. Journal of Chemical Education 2010;86(6):587-8.
- Oliver, Johnson. Ionic Radii for Spherical Potential Ions. Inorganic Chemistry 1973;12(4):780-85.
- Birkholz, Mario. Crystal-field induced dipoles in heteropolar crystals II: Physical significance. Z. Phys. 1995;96:333-40.
Problems
- Why are cations smaller and anions larger than their respective atoms?
- Cations are smaller than their respective atoms because of increased electron-electron repulsion
- Anions are larger than their respective atoms because of increased effective nuclear charge
- Cations are smaller than their respective atoms because of decreased electron-electron repulsion
- Anions are larger than their respective atoms because of decreased effective nuclear charge
- Which of the following are isoelectronic: \(F^-\), \(Cl^-\), \(Ca^{2+}\), \(Ar\)
- List the ions from smallest to largest: \(Se^{2-}\),\(Zr^{4+}\), \(Na^+\),\(Mg\), \(Rb^+\), \(Br^-\), \(K^+\)
- How are ionic radii measured?
- What are some of the problems with generalizing ionic trends?
Solution
- C & D: Cations are formed when an electron is lost. When this occurs there are less electron-electron repulsions and there is a greater net nuclear attraction per electron. So, the newly formed ion becomes a more condensed version of its neutral atom. Anions are formed when an electron is gained. When this occurs there are more electron-electron repulsions and there is a lower net nuclear attraction per electron. This will cause the electrons push each other away and spread out, causing the atom to become larger.
- Cl-, Ca2+, Ar all have 18 electrons; therefore, they are isoelectronic (F- has 10 electrons). An isoelectronic series is useful in understanding the effects of gained or loss electrons on atom size.
- Zr4+<K+<Rb+<Mg<Br-<Se2-: Ionic radii shorten with increasing positive charge and lengthen with increasing negative charge, and thus, anions are almost always larger than cations.
- Ionic radii are measured by proportioning ionic bond lengths between two ions within a crystal lattice. After studying many compounds, Linus Pauling found that the approximate ionic radii of O2- was 140pm. With this reference point, Pauling was able to calculate the ionic radii of other ions.
- Ionic radii are not fixed properties of ions. For the same ion, the radii can differ in different crystal lattices due certain variables such as coordination number and electron spin. Group Theory suggests that only ions in high-symmetric non-polar crystal lattices can accurately be measured for their radii.
Contributors and Attributions
- Michael H. Nguyen. University of California, Davis

