Periodic Properties of the Elements
- Page ID
- 617
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The elements in the periodic table are arranged in order of increasing atomic number. All of these elements display several other trends and we can use the periodic law and table formation to predict their chemical, physical, and atomic properties. Understanding these trends is done by analyzing the elements electron configuration; all elements prefer an octet formation and will gain or lose electrons to form that stable configuration.
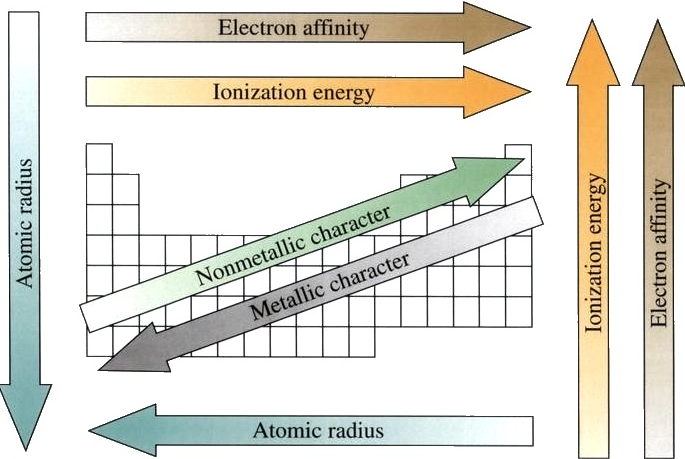
Atomic Radius
We can never determine the atomic radius of an atom because there is never a zero probability of finding an electron, and thus never a distinct boundary to the atom. All that we can measure is the distance between two nuclei (internuclear distance). A covalent radius is one-half the distance between the nuclei of two identical atoms. An ionic radius is one-half the distance between the nuclei of two ions in an ionic bond. The distance must be apportioned for the smaller cation and larger anion. A metallic radius is one-half the distance between the nuclei of two adjacent atoms in a crystalline structure. The noble gases are left out of the trends in atomic radii because there is great debate over the experimental values of their atomic radii. The SI units for measuring atomic radii are the nanometer (nm) and the picometer (pm). \(1 \, nm = 1 \times 10^{-9}\, m\) and \(1\, pm = 1 \times 10^{-12}\, m\).
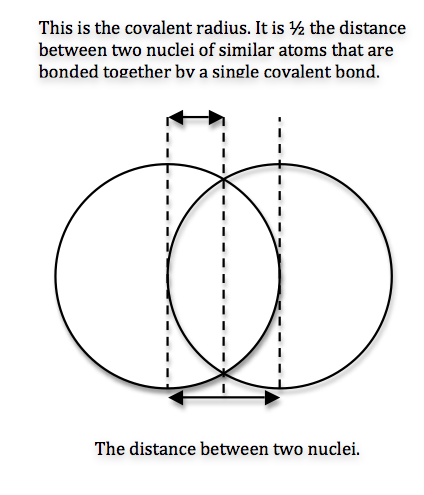
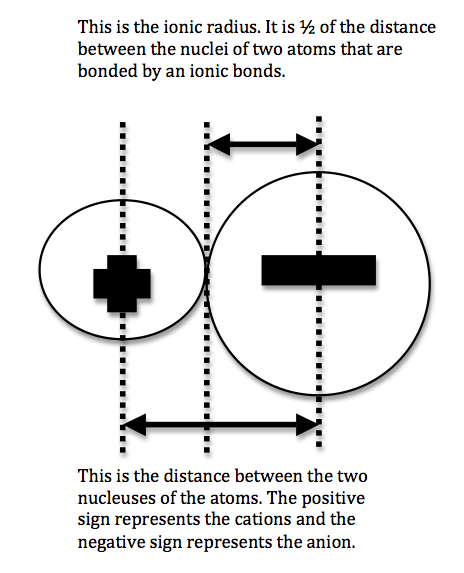
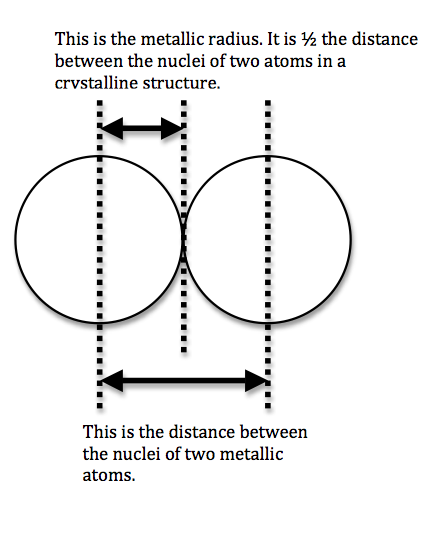
To explain this trend, the concept of screening and penetration must be understood. Penetration is commonly known as the distance that an electron is from the nucleus. Screening is defined as the concept of the inner electrons blocking the outer electrons from the nuclear charge. Within this concept we assume that there is no screening between the outer electrons and that the inner electrons shield the outer electrons from the total positive charge of the nucleus. In order to comprehend the extent of screening and penetration within an atom, scientists came up with the effective nuclear charge, \(Z_{eff}\). The equation for calculating the effective nuclear charge is shown below.
\[Z_{eff}= Z - S \nonumber \]
In the equation S represents the number of inner electrons that screen the outer electrons. Students can easily find S by using the atomic number of the noble gas that is one period above the element. For example, the S we would use for Chlorine would be 10 (the atomic number of Neon). Z is the total number of electrons in the atom. Since we know that a neutral atom has an identical number of protons and electrons, we can use the atomic number to define Z. For example, Chlorine would have a Z value of 17 (the atomic number of Chlorine). Continuing to use Chlorine as an example, the 10 inner electrons (S) would screen out the positive charge of ten protons. Therefore there would be and effective nuclear charge of 17-10 or +7. The effective nuclear charge shows that the nucleus is pulling the outer electrons with a +7 charge and therefore the outer electrons are pulled closer to the nucleus and the atomic radii is smaller. In summary, the greater the nuclear charge, the greater pull the nucleus has on the outer electrons and the smaller the atomic radii. In contrast, the smaller nuclear charge, the lesser pull the nucleus has on the outer electrons, and the larger atomic radii. Additionally, as the atomic number increases, the effective nuclear charge also increases. Figure 3 depicts the effect that the effective nuclear charge has on atomic radii.
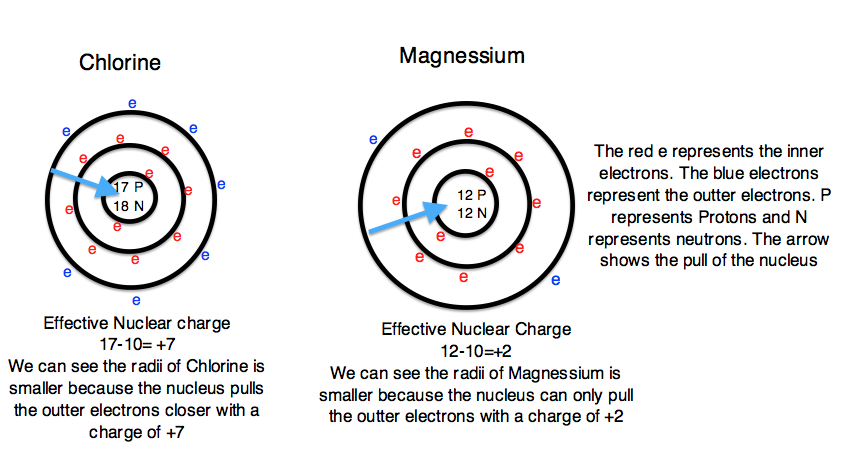
Now we are ready to describe the atomic radius trend in the periodic table. The atomic number increases moving left to right across a period and subsequently so does the effective nuclear charge. Therefore, moving left to right across a period the nucleus has a greater pull on the outer electrons and the atomic radii decreases. Moving down a group in the periodic table, the number of filled electron shells increases. In a group, the valence electrons keep the same effective nuclear charge, but now the orbitals are farther from the nucleus. Therefore, the nucleus has less of a pull on the outer electrons and the atomic radii are larger.
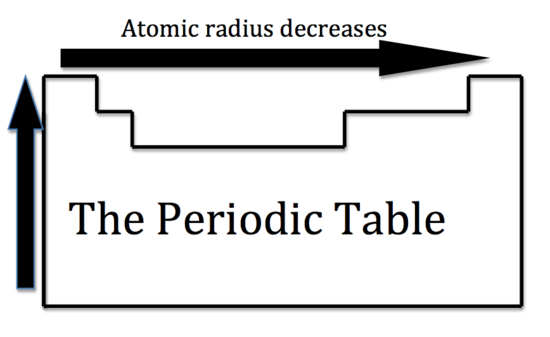
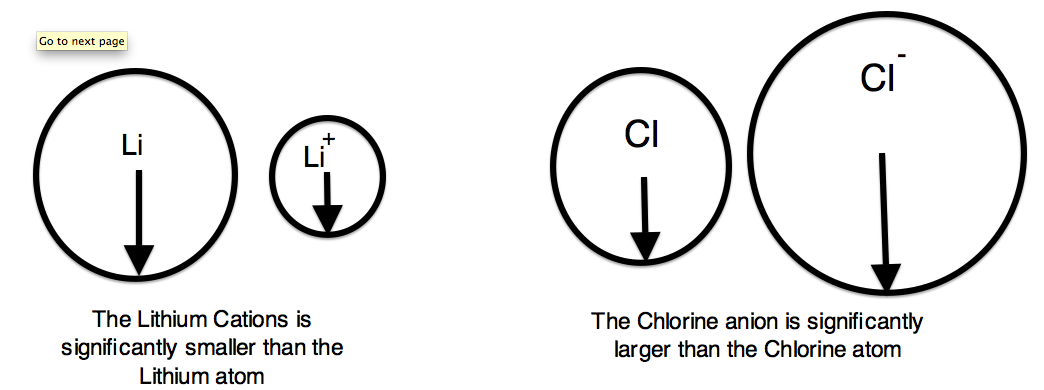
We can now use these concept to explain the atomic radius differences of cations and anions. A cation is an atom that has lost one of its outer electrons. Cations have a smaller radius than the atom that they were formed from. With the loss of an electron, the positive nuclear charge out powers the negative charge that the electrons exert. Therefore, the positive nucleus pulls the electrons tighter and the radius is smaller. An anion is an atom that has gained an outer electron. Anions have a greater radius than the atom that they were formed from. The gain of an electron does not alter the nuclear charge, but the addition of an electron causes a decrease in the effective nuclear charge. Therefore, the electrons are held more loosely and the atomic radius is increased.
Ionization Energy (ionization potential)
Expelling an electron from an atom requires enough energy to overcome the magnetic pull of the positive charge of the nucleus. Therefore, ionization energy (I.E. or I) is the energy required to completely remove an electron from a gaseous atom or ion. The Ionization Energy is always positive.
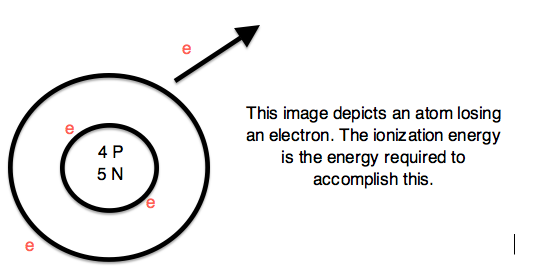
The energy required to remove one valence electron is the first ionization energy, the second ionization energy is the energy required to remove a second valence electron, and so on.
- 1st ionization energy
\[\ce{Na(g) -> Na^{+}(g) + e^{-}(g)} \nonumber \]
- 2nd ionization energy
\[\ce{ Na^{+}(g) -> Na^{2+}(g) + e^{-}} \nonumber \]
Ionization energies increase relative to high effective charge. The highest ionization energies are the noble gases because they all have high effective charge due to their octet formation and require a high amount of energy to destroy that stable configuration. The highest amount of energy required occurs with the elements in the upper right hand corner. Additionally, elements in the left corner have a low ionization energy because losing an electron allows them to have the noble gas configuration. Therefore, it requires less energy to remove one of their valence electrons
| Element | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Na | 496 | 4562 | |||||
| Mg | 738 | 1451 | 7733 | ||||
| Al | 577 | 1817 | 2745 | 11580 | |||
| Si | 786 | 1577 | 3232 | 4356 | 16090 | ||
| P | 1060 | 1903 | 2912 | 4957 | 6274 | 21270 | |
| S | 999.6 | 2251 | 3361 | 4564 | 7013 | 8496 | 27110 |
| Cl | 1256 | 2297 | 3822 | 5158 | 6542 | 9362 | 11020 |
| Ar | 1520 | 2666 | 3931 | 5771 | 7238 | 8781 | 12000 |
These are the ionization energies for the period three elements. Notice how Na after in the second I.E, Mg in the third I.E., Al in the fourth I.E., and so on, all have a huge increase in energy compared to the proceeding one. This occurs because the proceeding configuration was in a stable octet formation; therefore it requires a much larger amount of energy to ionize.
Ionization Energies increase going left to right across a period and increase going up a group. As you go up a group, the ionization energy increases, because there are less electron shielding the outer electrons from the pull of the nucleus. Therefore, it requires more energy to out power the nucleus and remove an electron. As we move across the periodic table from left to right, the ionization energy increases , due to the effective nuclear charge increasing. This is because the larger the effective nuclear charge, the stronger the nucleus is holding onto the electron and the more energy it takes to release an electron.

The ionization energy is only a general rule. There are some instances when this trend does not prove to be correct. These can typically be explained by their electron configuration. For example, Magnesium has a higher ionization energy than Aluminum. Magnesium has an electron configuration of [Ne]3s2. Magnesium has a high ionization energy because it has a filled 3s orbital and it requires a higher amount of energy to take an electron from the filled orbital.
Electron Affinity
Electron affinity (E.A.) is the energy change that occurs when an electron is added to a gaseous atom. Electron affinity can further be defined as the enthalpy change that results from the addition of an electron to a gaseous atom. It can be either positive or negative value. The greater the negative value, the more stable the anion is.
- (Exothermic) The electron affinity is positive
\[\ce{X(g) + e^{-} -> X^{-} + Energy} \nonumber \]
- (Endothermic) The electron affinity is negative
\[\ce{X(g) + e^{-} + Energy -> X^{-}} \nonumber \]
It is more difficult to come up with trends that describe the electron affinity. Generally, the elements on the right side of the periodic table will have large negative electron affinity. The electron affinities will become less negative as you go from the top to the bottom of the periodic table. However, Nitrogen, Oxygen, and Fluorine do not follow this trend. The noble gas electron configuration will be close to zero because they will not easily gain electrons.

Electronegativity
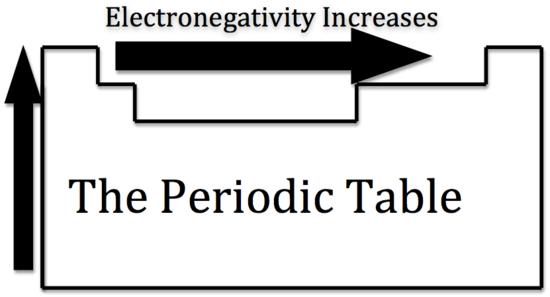
Electronegativity is the measurement of an atom to compete for electrons in a bond. The higher the electronegativity, the greater its ability to gain electrons in a bond. Electronegativity will be important when we later determine polar and nonpolar molecules. Electronegativity is related with ionization energy and electron affinity. Electrons with low ionization energies have low electronegativities because their nuclei do not exert a strong attractive force on electrons. Elements with high ionization energies have high electronegativities due to the strong pull exerted by the positive nucleus on the negative electrons. Therefore the electronegativity increases from bottom to top and from left to right.
Metallic Character
The metallic character is used to define the chemical properties that metallic elements present. Generally, metals tend to lose electrons to form cations. Nonmetals tend to gain electrons to form anions. They also have a high oxidation potential therefore they are easily oxidized and are strong reducing agents. Metals also form basic oxides; the more basic the oxide, the higher the metallic character.

As you move across the table from left to right, the metallic character decreases, because the elements easily accept electrons to fill their valance shells. Therefore, these elements take on the nonmetallic character of forming anions. As you move up the table, the metallic character decreases, due to the greater pull that the nucleus has on the outer electrons. This greater pull makes it harder for the atoms to lose electrons and form cations.
Other Trends
Melting Points: Trends in melting points and molecular mass of binary carbon-halogen compounds and hydrogen halides are due to intermolecular forces. Melting destroys the arrangement of atoms in a solid, therefore the amount of heat necessary for melting to occur depends on the strength of attraction between the atoms. This strength of attraction increases as the number of electrons increase. Increase in electrons increases bonding.
Example: Melting point of HF should be approximately -145 °C based off melting points of HCl, HBr, and HI, but the observed value is -83.6°C.
Heat and electricity conductibility vary regularly across a period. Melting points may increase gradually or reach a peak within a group then reverse direction.
Example: Third period elements Na, Mg, and Al are good conductors of heat and electricity while Si is only a fair conductor and the nonmetals P, S, Cl and Ar are poor conductors.
Redox Potentials
Oxidation Potential
Oxidation is a reaction that results in the loss of an electron. Oxidation potential follows the same trends as the ionization energy. That is because the smaller the ionization energy, the easier it is to remove an electron. (e.g)
\[K_{(s)} \rightarrow K^+ + e^- \nonumber \]
Reduction Potential
Reduction is a reaction that results in the gaining of an electron. Reduction potentials follow the same trend as the electron affinity. That is because the larger, negative electron affinity, the easier it is to give an electron. Example of Reduction:
\[F_{(s)} + e^- \rightarrow F^- \nonumber \]
Uses in knowing the Periodic Properties of Elements
- Predicting greater or smaller atomic size and radial distribution in neutral atoms and ions
- Measuring and comparing ionization energies
- Comparing electron affinities and electronegativities
- Predicting redox potential
- Comparing metallic character with other elements; its ability to form cations
- Predicting what reaction may or may not occur due to the trends
- Determining greater cell potential (sum of oxidation and reduction potential) between reactions
- Completing chemical reactions according to trends
Summary of Periodic Trends
The Periodic Table of Elements categorizes like elements together. Dmitri Mendeleev, a Russian scientist, was the first to create a widely accepted arrangement of the elements in 1869. Mendeleev believed that when the elements are arranged in order of increasing atomic mass, certain sets of properties recur periodically. Although most modern periodic tables are arranged in eighteen groups (columns) of elements, Mendeleev's original periodic table had the elements organized into eight groups and twelve periods (rows).
On the periodic table, elements that have similar properties are in the same groups (vertical). From left to right, the atomic number (z) of the elements increases from one period to the next (horizontal). The groups are numbered at the top of each column and the periods on the left next to each row. The main group elements are groups 1,2 and 13 through 18. These groups contain the most naturally abundant elements, and are the most important for life. The elements shaded in light pink in the table above are known as transition metals. The two rows of elements starting at z=58, are sometimes called inner transition metals and have that have been extracted and placed at the bottom of the table, because they would make the table too wide if kept continuous. The 14 elements following lanthanum (z=57) are called lanthanides, and the 14 following actinium (z=89) are called actinides.
Elements in the periodic table can be placed into two broad categories, metals and nonmetals. Most metals are good conductors of heat and electricity, are malleable and ductile, and are moderate to high melting points. In general, nonmetals are nonconductors of heat and electricity, are nonmalleable solids, and many are gases at room temperature. Just as shown in the table above, metals and nonmetals on the periodic table are often separated by a stairstep diagonal line, and several elements near this line are often called metalloids (Si, Ge, As, Sb, Te, and At). Metalloids are elements that look like metals and in some ways behave like metals but also have some nonmetallic properties. The group to the farthest right of the table, shaded orange, is known as the noble gases. Noble gases are treated as a special group of nonmetals.
Alkali Metals/Alkali Earth Metals
The Alkali metals are comprised of group 1 of the periodic table and consist of Lithium, Sodium, Rubidium, Cesium, and Francium. These metals are highly reactive and form ionic compounds (when a nonmetal and a metal come together) as well as many other compounds. Alkali metals all have a charge of +1 and have the largest atom sizes than any of the other elements on each of their respective periods.
Alkali Earth Metals are located in group 2 and consist of Beryllium, Magnesium, Calcium, Strontium, Barium, and Radium. Unlike the Alkali metals, the earth metals have a smaller atom size and are not as reactive. These metals may also form ionic and other compounds and have a charge of +2.
Transition Metals
The transition metals range from groups IIIB to XIIB on the periodic table. These metals form positively charged ions, are very hard, and have very high melting and boiling points. Transition metals are also good conductors of electricity and are malleable.
Lanthanides and Actinides
Lanthanides (shown in row ** in chart above) and Actinides (shown in row * in chart above), form the block of two rows that are placed at the bottom of the periodic table for space issues. These are also considered to be transition metals. Lanthanides are form the top row of this block and are very soft metals with high boiling and melting points. Actinides form the bottom row and are radioactive. They also form compounds with most nonmetals. To find out why these elements have their own section, check out the electron configurations page.
Metalloids
As mentioned in the introduction, metalloids are located along the staircase separating the metals from the nonmetals on the periodic table. Boron, silicon, germanium, arsenic, antimony, and tellurium all have metal and nonmetal properties. For example, Silicon has a metallic luster but is brittle and is an inefficient conductor of electricity like a nonmetal. As the metalloids have a combination of both metallic and nonmetal characteristics, they are intermediate conductors of electricity or "semiconductors".
Halogens
Halogens are comprised of the five nonmetal elements Flourine, Chlorine, Bromine, Iodine, and Astatine. They are located on group 17 of the periodic table and have a charge of -1. The term "halogen" means "salt-former" and compounds that contain one of the halogens are salts. The physical properties of halogens vary significantly as they can exist as solids, liquids, and gases at room temperature. However in general, halogens are very reactive, especially with the alkali metals and earth metals of groups 1 and 2 with which they form ionic compounds.
Noble Gases
The noble gases consist of group 18 (sometimes reffered to as group O) of the periodic table of elements. The noble gases have very low boiling and melting points and are all gases at room temperature. They are also very nonreactive as they already have a full valence shell with 8 electrons. Therefore, the noble gases have little tendency to lose or gain electrons.
Useful Relationships from the Periodic Table
The periodic table of elements is useful in determining the charges on simple monoatomic ions. For main-group elements, those categorized in groups 1, 2, and 13-18, form ions they lose the same number of electrons as the corresponding group number to which they fall under. For example, K atoms (group 1) lose one electron to become K+ and Mg atoms (group 2) lose two electrons to form Mg2+. The other main-group elements found in group 13 and higher form more than one possible ion.
The elements in groups 3-12 are called transition elements, or transition metals. Similar to the main-group elements described above, the transition metals form positive ions but due to their capability of forming more than two or more ions of differing charge, a relation between the group number and the charge is non-existent.
Arrange these elements according to decreasing atomic size: Na, C, Sr, Cu, Fr
- Answer
-
Fr, Sr, Cu, Na, C
Arrange these elements according to increasing negative E. A.: Ba, F, Si, Ca, O
- Answer
-
Ba, Ca, Si, O, F
Arrange these elements according to increasing metallic character: Li, S, Ag, Cs, Ge
- Answer
-
Li, S, Ge, Ag, Cs
Which reaction do you expect to have the greater cell potential?
- \(\ce{2Na(s) + Cl2(g)→ 2NaCl(s) or 2Cs(s) +Cl2(g) → 2RbCl(s)\)
- \(\ce{2Na(s) + Cl2(g)→ 2NaCl(s) or Be(s) + Cl2(g) → BeCl2(s)}\)
- Answer
-
Second equation
First equation
Which equation do you expect to occur?
- \(\ce{I2(s) + 2Br (aq) → Br2(l) + 2I(aq)}\)
- \(\ce{Cl2(g) + 2I (aq) → I2 (s) + 2Cl(aq)}\)
- Answer
-
5. A) Yes
B) No
Problems
*Highlight Answer:_____ to view answers.
1. An element that is an example of a metalloid is (a) S; (b) Zn; (c) Ge; (d) Re; (e) none of these
Answer: (c) Ge
2. In the periodic table, the vertical (up and down) columns are called (a) periods; (b) transitions; (c) families/groups; (d) metalloids; (e) none of these.
Answer: (c) families/groups
3. Why are noble gases inert (nonreactive)?
Answer: Noble gases are inert because they already have a full valence electron shell and have little tendency to gain or lose electrons.
4. What are compounds that contain a halogen called?
Answer: Salts
5. Lanthanides and Actinides are: (a) alkali earth metals; (b) transition metals; (c) metalloids; (d) alkali metals; (e) none of these
Answer: (b) transition metals
References
- Cotton, F.A.; Wilkinson, G. (1988). Advanced Inorganic Chemistry (5th Edn). New York: Wiley. ISBN 0-471-84997p. 1385.
- Hutchinson, John. "Journal of Chemical Education." Concept Development Studies in Chemistry (2007). Print. Outside Links
- Jolly, William L. (1991). Modern Inorganic Chemistry (2nd Edn.). New York: McGraw-Hill. ISBN 0-07-112651-1.
- Petrucci, Ralph H. General Chemistry. 9th ed. New Jersey: Pearson Prentice Hall, 2005.

