1.17: Jahn-Teller Distortions
- Page ID
- 204718
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction to Jahn-Teller Distortion
The Jahn–Teller effect occurs because the unequal occupation of orbitals with identical energies is unfavorable. To avoid these unfavorable electronic configurations, molecules distort (lowering their symmetry) to render these orbitals no longer degenerate.[1] The Jahn–Teller distortion, describes the geometrical distortion of molecules and ions that result from certain electron configurations.[2] This distortion is normally observed among octahedral complexes where the two axial bonds can be compressed or elongated to result in a different bond length from those of the equatorial bonds as shown in Figure \(\PageIndex{1}\).[3]
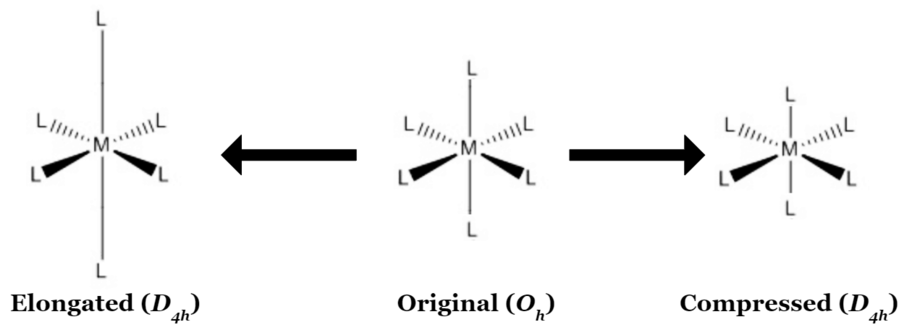
In 1937, Hermann Jahn and Edward Teller postulated a theorem stating that "stability and degeneracy are not possible simultaneously unless the molecule is a linear one," in regards to its electronic state. This leads to a break in degeneracy which stabilizes the molecule and by consequence, reduces its symmetry.[4]
Orbital Analysis of Jahn-Teller Distortion
Elongation Distortion
Elongation as shown in Figure \(\PageIndex{2}\), is the most common mechanism of distortion. In ideally octahedral complexes that experience Jahn–Teller distortion, the eg* orbitals change more in energy relative to the t2g orbitals.[5]
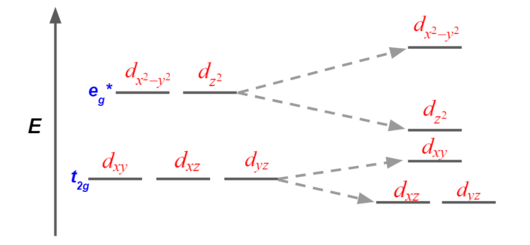
When the octahedral complex undergoes an elongation, any of the metal d orbitals that carry a z-directional feature become lower in energy, ligands are easier to bond along z-direction. Geometrically, as the z-direction gets elongated, the repulsion energy and sterical hindrance along z-direction are lower to allow ligands easier to bond.
Compression Distortion
Compression as shown in Figure \(\PageIndex{3}\), happens less frequently than the elongation.
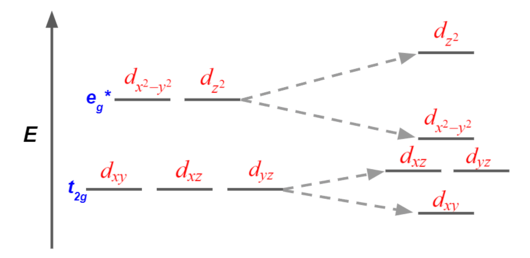
When the octahedral complex undergoes a compression, any of the metal d orbitals that carry a z-directional feature become higher in energy, ligands are harder to bond along z-direction. Geometrically, as the z-direction gets compressed, the repulsion energy and sterical hindrance along z-direction are higher, which makes ligands more difficult to bond.
d-orbitals and their associated Jahn-Teller Distortion
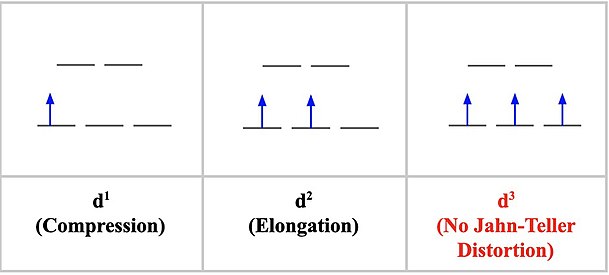
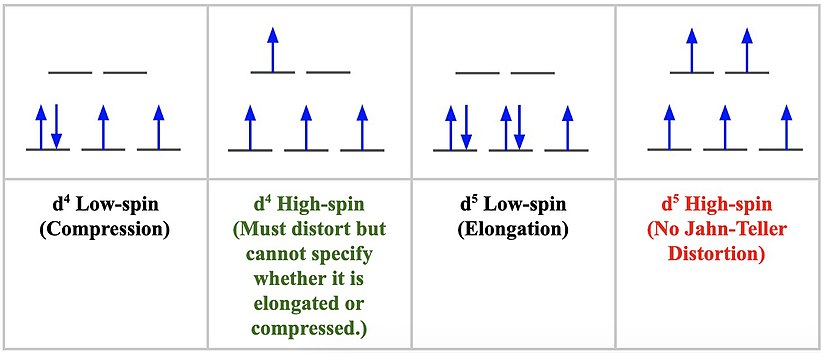
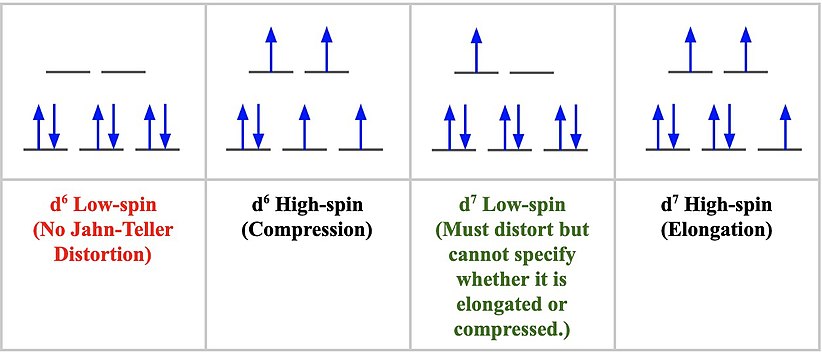
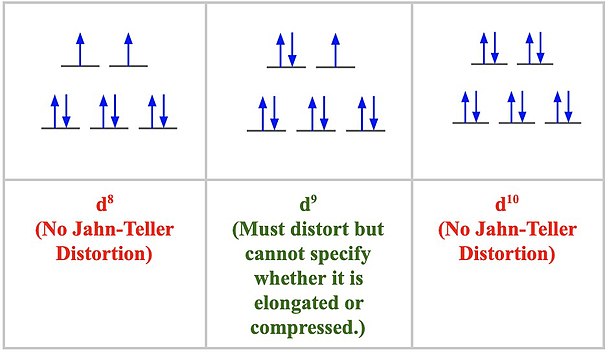
The Strength of Jahn-Teller Distortion
General Strength Trend of Jahn-Teller Distortion
For octahedral complexes:
- weak Jahn-Teller effect if t2g is unevenly occupied
- strong Jahn-Teller effect if eg is unevenly occupied
Table of Jahn-Teller Distortion Strength[6]

Jahn-Teller Distortion and Spectra
Spectra of the First-order Jahn-Teller Distortion
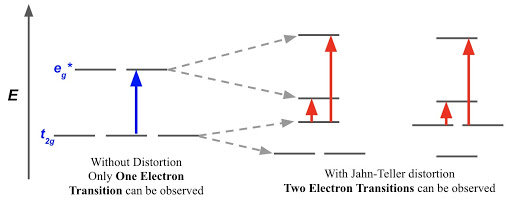
In the first-order Jahn-Teller distortion, two electron transitions can be observed. This phenomenon can lead to a “double-hump” result on the absorption spectra as shown in Figure \(\PageIndex{5}\) and \(\PageIndex{6}\).
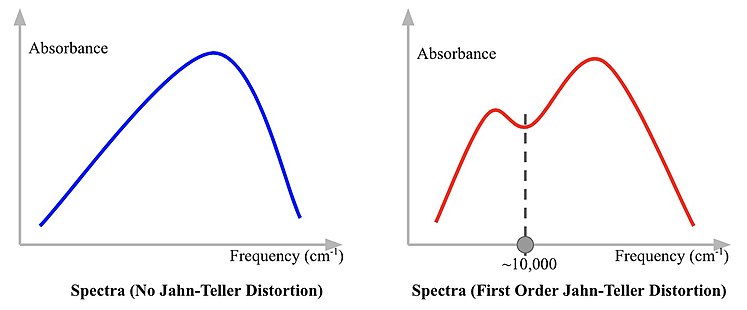
The Second-order Jahn-Teller Distortion
A brief introduction to the Second-order Jahn-Teller Distortion
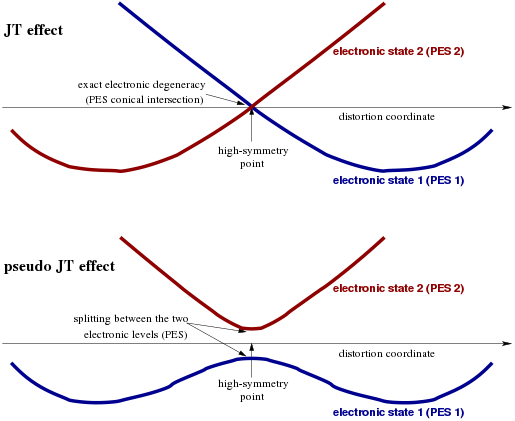
The second order Jahn-Teller distortion occurs when the excited state of the transition metal has unequal occupation of d-orbitals with identical energies.[7] The ground state of the transition metal may not have unequal occupation of degenerate orbitals, therefore, the second order Jahn-Teller distortion is also called Pseudo Jahn-Teller distortion as shown in Figure \(\PageIndex{7}\).[8]
Spectra of the Second-order Jahn-Teller Distortion
Since the second order Jahn-Teller distortion occurs in excited state, the trough on the spectra likely located at higher frequency, thus higher in energy, as shown in Figure \(\PageIndex{8}\).
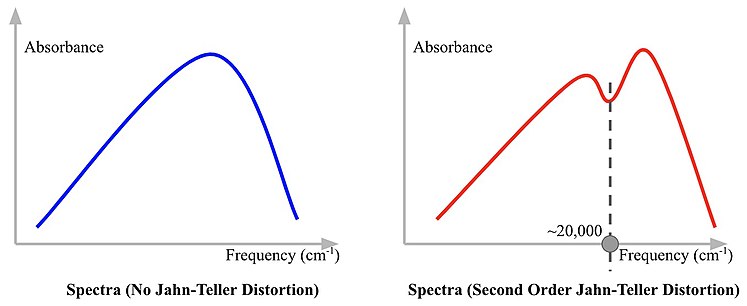
Figure \(\PageIndex{8}\).
References
- Libretexts. “Jahn-Teller Distortions.” Chemistry LibreTexts, Libretexts, 23 Apr. 2019,
- Libretexts. “5.7: Jahn-Teller Effect.” Chemistry LibreTexts, Libretexts, 23 Apr. 2019
- Libretexts. “Jahn-Teller Distortions.” Chemistry LibreTexts, Libretexts, 23 Apr. 2019
- “Jahn–Teller Effect.” Wikipedia, Wikimedia Foundation, 7 Mar. 2019
- Libretexts. “Jahn-Teller Distortions.” Chemistry LibreTexts, Libretexts, 23 Apr. 2019
- Miessler, Gary L., et al. Inorganic Chemistry. Pearson, 2014.
- Bersuker, Isaac B. (9 January 2013). "Pseudo-Jahn–Teller Effect—A Two-State Paradigm in Formation, Deformation, and Transformation of Molecular Systems and Solids". Chemical Reviews. American Chemical Society (ACS). 113 (3): 1351–1390. doi:10.1021/cr300279n. ISSN 0009-2665.
- “File:Jahn-Teller and Pseudo Jahn-Teller Effects.svg.” File:Jahn-Teller and Pseudo Jahn-Teller Effects.svg - Wikimedia Commons


