1.7: Diatomic Molecular Orbitals
- Page ID
- 204708
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The simplicity of diatomic molecular orbitals allows for their inspection using the theory of linear combinations of atomic orbitals (LCAO). As two atoms approach each other, their atomic orbitals overlap. In order to form bonding molecular orbitals, sufficient overlap should occur between atomic orbitals and they must have similar energies and matching symmetries. Anti-bonding molecular orbitals occur when two atomic orbitals cancel each other out. This gives rise to a node or area with zero electron density in between the two atoms.
Molecular Orbitals
Just like the atomic orbitals, molecular orbitals(MO) are used to describe the bonding in molecules by applying the group theory. The basic thought of what is molecular orbitals can be the organized combinations of the atomic orbitals according to the symmetry of the molecules and the characteristics of atoms. By applying the MO diagram, the properties such as magnetism and chirality of the molecules can be predicted.
Just like atomic orbitals can be solved as wavefunctions by applying Hermitian Operator to Schrödinger equations, molecule orbitals can be approximated by the linear combinations of atomic orbitals(LCAO):
\[
\Psi=\sum_{n=0}^{\mathrm{N}} c_{i} \psi_{i}
\nonumber \]
is the molecular wave function, \({\displaystyle \psi }\) is the atomic wave functions for atoms, \({\displaystyle c_{i}}\) is the adjustable coefficients. This means that when the atoms get closer to each other, their atomic orbitals can overlap and the probability of the occurring of the electrons from the atoms becomes significantly in the overlap regions, which is the formation of the molecular orbitals.
Bonding, Anti-bonding and Non-bonding Molecular Orbitals
Before it goes further, some acknowledge about bonding and anti-bonding should be emphasized. When two atomic orbitals overlap, they can form new orbitals in two ways: one is the bonding orbital and another one is the anti-bonding orbital. In a molecular orbital diagram, if atomic orbitals form a bonding orbital, they must form an anti-bonding orbital. The bonding orbitals and anti-bonding orbitals always have the same number and relate with each other. For example, if there is a 1σ bonding orbital, then there must be a 1σ*, which is the relevant anti-bonding orbital of 1σ, where * is used to represent anti-bonding. This bonding and anti-bonding orbitals caused by the different ways of overlapping of the atomic orbitals.
Besides the bonding and anti-bonding molecular orbitals, there can also be some non-bonding orbitals. These orbitals only exist when some atomic orbitals of an atom cannot find any atomic orbital from another atom that has the same symmetry properties, then these atomic orbitals will remain at the same energy and form no bond. That’s why they are called “non-bonding” molecular orbitals.
Diatomic Molecular Orbitals
Normally, in diatomic molecular orbitals, the atomic orbitals with the closest energy level can overlap with each other and form molecular orbitals. Therefore, the atomic orbitals generally tend to overlap one by one from the lowest potential energy to the highest potential energy. For example, in a homonuclear diatomic molecule, which means that both atoms are the same element, the same orbitals will overlap together and form molecular orbitals.
Eg. in the oxygen O2, the 1s orbital will overlap with 1s orbital to form a σ orbital and a σ* orbital and the 2s orbital will overlap with 2s orbital to form a σ orbital and a σ* orbital. The 1s orbital cannot overlap with 2s orbital in this case.
For another example, in a heteronuclear diatomic molecule, which means that the atoms in the molecule are different elements, the orbitals with the closest energy can overlap with each other and form molecular orbitals.
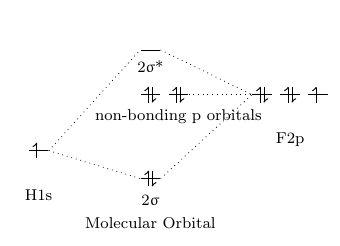
Eg. in the hydrogen fluoride HF, hydrogen's 1s orbital will overlap with one of the fluorine's 2p orbitals to form a σ orbital and a σ* orbital since the orbital potential energy of H1s orbital is -13.61eV and of F2p is -18.65eV. Comparing with F2s orbital which has -40.17eV as its orbital potential energy, they are really close to each other. That's why H1s will form molecular orbitals with F2p instead of F2s.[1]
Also notice that only two atomic orbitals with similar symmetry properties can combine together. For example, s orbital can’t overlap with px orbital if the overlap equally with both the same and opposite signs, this will cancel the bonding and anti-bonding effect which will result in no molecular orbital forms.
Besides that, we normally only consider the valence atomic orbitals. That's why the F1s orbital does not be considered here since it's full-filled.
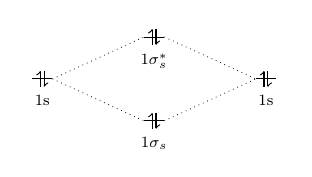
MO from s Orbitals
The overlap of two s orbitals will form a σ orbital and a σ* orbital.
MO from p Orbitals
The overlap of two p orbitals will form either a σ and a σ* orbitals or a π and a π*orbitals. Generally, we choose to assign the z axis of two atoms point to each other which allows the pz orbitals overlap “head” to “head” and form σ and σ* orbitals. This also allows the px orbitals overlap “side” to “side” and form π and π*orbitals. This also applies for the py orbitals.
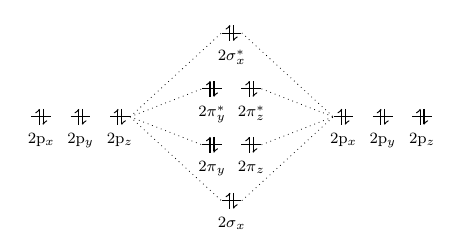
Sometimes, when p orbitals can’t find another orbital has a similar symmetry with it, these p orbitals will remain as non-bonding orbitals.
MO from d Orbitals
Start from the third row, all the elements after sodium (Na) have d orbitals. There are totally 5 d orbitals, which are named as dz2,dxy,dxz,dyz and dx2-y2. Elements with d orbitals, especially the transition metals, can also form bonds by using d orbitals. As shown in Figure \(\PageIndex{4}\), the different overlap of the d orbitals will result in different electron density, which results in different types of bonds. Just like what happens to the p-orbital-overlapping molecular orbitals, d atomic orbitals can also overlap with other orbitals in different orbital potential energy levels such as p orbitals and s orbitals. This is also the reason for the formation of a metal complex. However, d orbitals normally are not applied to form molecular orbitals in a diatomic molecule.
Nonbonding Orbitals
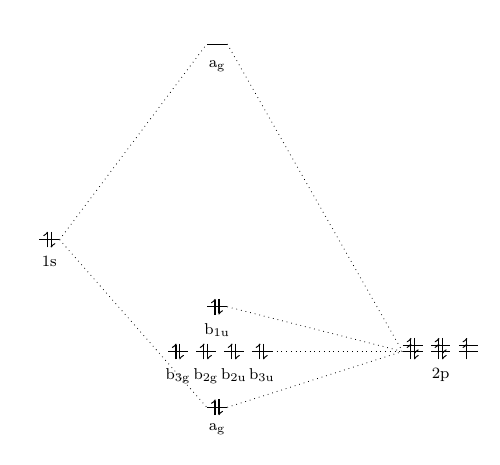
As mentioned before, if an atomic orbital cannot find any other orbital with similar symmetry, then it will remain as non-bonding molecular orbital. The non-bonding molecular orbitals normally have the same energies as the atomic orbitals that form them, although there are some special cases can happen (not in diatomic MO, but in some metal complex). For example, in the ion FHF-, by solving the irreducible representation, it can be found that the base of FHF- has ag, b2u, b3u, b2g, b3g and b1u. However, since the H atom has only a 1s orbital, it can only form molecular orbitals with ag. Therefore, b2u, b3u, b2g, b3g and b1u will remain as non-bonding molecular orbitals. Also, notice that b1u has a higher level in energy state. This can be caused by the extreme unsymmetrical structure of this molecular orbital. Another guess of the increase in the b1u energy level can be the slightly mixing with the 2s orbital from two fluorines.
Orbital Mixing
This is the most tricky part for the diatomic molecular orbitals. In general, we only consider the interactions between atomic orbitals have the same energies unless there is no atomic orbital satisfy the request. However, the interaction between two atomic orbitals with relatively close energies that have the same symmetry can also happen. This will result in the raising of the energies of the molecular orbitals.
Considering Figure \(\PageIndex{2}\) above, this is an example without interaction between two atomic orbitals with close energies that have the same symmetry. The \({\displaystyle \pi _{u}}\) molecular orbitals have higher energy than the \({\displaystyle \sigma _{g}}\) molecular orbital. However, since the \({\displaystyle \sigma _{g}(2s)}\) and \({\displaystyle \sigma _{g}(2p)}\) orbitals both have \({\displaystyle \sigma _{g}}\) symmetry,these orbitals can interat to lower the energy of the \({\displaystyle \sigma _{g}(2s)}\) and to increase the energy of the \({\displaystyle \sigma _{g}(2p)}\). This will result the energy of \({\displaystyle \sigma _{g}(2p)}\) orbital has higher energy than \({\displaystyle \pi _{u}(2p)}\) orbitals, as shown in Figure \(\PageIndex{7}\). This phenomenon is called mixing.
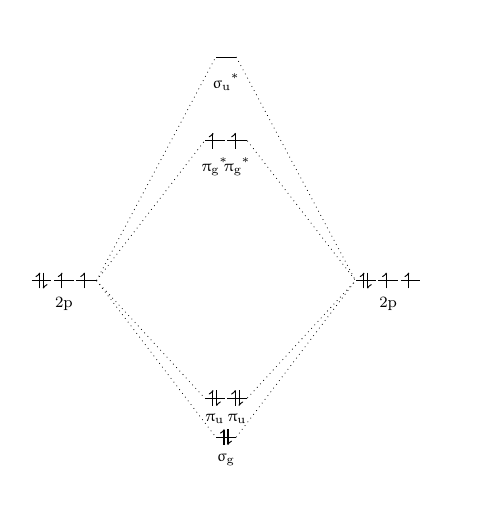
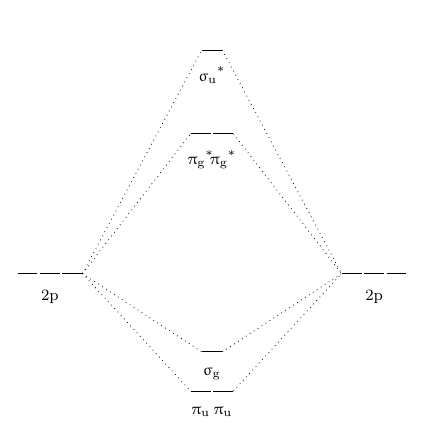
For example, this s-p mixing will happen for B2 and C2.
Heteronuclear Diatomic Molecule
Unlike the homonuclear diatomic molecule, many heteronuclear diatomic molecules are polar molecules. This means that the electron density does not evenly distribute over each atom. The electron density always favors the atom that is more electronegative. MO theory can also be applied in this situation.
As mentioned before, since here we deal with different two elements in molecules, the orbital potential energies will be considered. This will result in uneven contributions of molecular orbitals from the overlap of the atomic orbitals. Fortunately, farther the two atomic potential energies (APE) are, less the magnitude of the interaction between them. This means that only two atomic orbitals with similar energies can overlap enough to form molecular orbitals. Use the example of HF (Figure \(\PageIndex{3}\)). According to Table \(\PageIndex{1}\), 1s orbital of the hydrogen atom has APE as -13.61eV, 2s orbital of fluorine has APE as -40.17eV and 2p orbitals of fluorine have APE as -18.65eV. It is obvious that \({\displaystyle H1s}\) orbital has a much closer potential energy to the \({\displaystyle F2p}\) instead of \({\displaystyle F2s}\). Therefore, \({\displaystyle H1s}\) orbital overlaps much more with \({\displaystyle F2p}\) and form molecular orbitals. \({\displaystyle F2s}\) will remain as a non-bonding orbital.
| Atomic Number | Elemment | 1s | 2s | 2p | 3s | 3p | 4s |
| 1 | H | -13.61 | |||||
| 2 | He | -24.59 | |||||
| 3 | Li | -5.39 | |||||
| 4 | Be | -9.32 | |||||
| 5 | B | -14.05 | -8.3 | ||||
| 6 | C | -19.43 | -10.66 | ||||
| 7 | N | -25.56 | -13.18 | ||||
| 8 | O | -32.38 | -15.85 | ||||
| 9 | F | -40.17 | -18.65 | ||||
| 10 | Ne | -48.47 | -21.59 | ||||
| 11 | Na | -5.14 | |||||
| 12 | Mg | -7.65 | |||||
| 13 | Al | -11.32 | -5.98 | ||||
| 14 | Si | -15.89 | -7.78 | ||||
| 15 | P | -18.84 | -9.65 | ||||
| 16 | S | -22.71 | -11.62 | ||||
| 17 | Cl | -25.23 | -13.67 | ||||
| 18 | Ar | -29.24 | -15.82 | ||||
| 19 | K | -4.34 | |||||
| 20 | Ca | -6.11 |
Drawing Diatomic MO Diagram
Here are some common steps to help you draw the diatomic MO diagram.
- Recognize the diatomic molecule is a homonuclear molecule or heteronuclear molecule;
- Recognize the orbital potential energies of their valence atomic orbitals, find the closest pair;
- Recognize the symmetry of these atomic orbitals to Figure out if the interaction can actually happen. Then determine the {\displaystyle \sigma } and {\displaystyle \pi } bonding and anti-bonding, and even non-bonding orbitals;
- Recognize the mixing effect to see if there are any energy shift for the molecular orbitals;
- Draw the electrons from the lowest molecular orbital. Follow the rules like the Pauli exclusion principle to draw the ground state MO diagram.
Reference
- Miessler, Gary. “Chapter 5. Molecular Orbital Theory.” Inorganic Chemistry, by Gary L. Miessler et al., Pearson, 2014, pp. 117–138.
- Greeves, Nick. “ChemTube3D.” ChemTube3D. [1]


