6.26: Steady State Diffusion, Diffusion Coefficient, Fick’s Second Law

Steady state diffusion

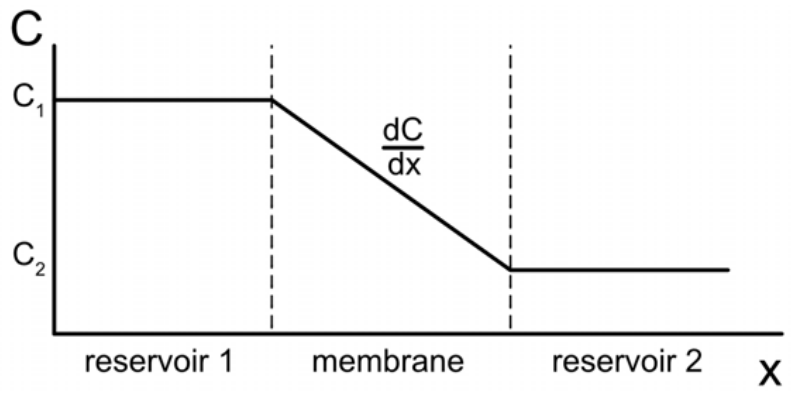
Diffusion refers to the net movement of a species down a concentration gradient, from an area of high concentration to an area of low concentration. Importantly, diffusion can take place in any phase of matter, including in solids! Steady state (time independent) diffusion is described by Fick’s first law:

\(J=-D \dfrac{d C}{d x}\)

Here, \(\mathrm{J}\) is the diffusion flux: the rate at which an amount of a substance passes through a surface area. The diffusion flux has units of \(\frac{\text { amount }}{\text { areaxtime }}\), or \(\frac{\mathrm{mol}}{\mathrm{m}^2 s}\). \(\mathrm{D}\) is the diffusion coefficient, which is sometimes called diffusivity. It depends on the specific circumstances the diffusion is occurring in, including what materials are involved and the state of the surrounding environment. It has units of \(\frac{m^2}{s}\). Finally, here \(\mathrm{C}\) is concentration ( \(M\) or \(\frac{\mathrm{mol}}{\text { volume }}\), so \(\frac{d C}{d x}\) is the change in concentration with respect to change in position. Therefore, Fick's first law tells us how concentration change flows over the region between two different concentrations.

Example: If you heat steel in a carbon rich atmosphere, carbon atoms will diffuse into the steel, hardening it. Calculate the diffusivity of a steel plate if the flux of carbon atoms through the plate is \(2 \times 10^{-6} \frac{g}{m^2 s}\), the concentration \(2 \mathrm{~mm}\) under the surface is \(300 \frac{g}{m^3}\), and the concentration \(5 \mathrm{~mm}\) under the surface is \(100 \frac{g^3}{m^3}\).

Answer

We can rearrange Fick’s First law and plug in:

\begin{gathered}
D=-J\left(\dfrac{d C}{d x}\right)^{-1}=-J\left(\dfrac{x_2-x_1}{C_2-C_1}\right)=-2 \times 10^{-6} \dfrac{g}{m^2 s}\left(\dfrac{\left(2 \times 10^{-3}-5 \times 10^{-3}\right) m}{\left(3 \times 10^2-1 \times 10^2\right) \frac{g}{m^3}}\right) \\
D=3 \times 10^{-11} \dfrac{m^2}{\mathrm{~s}}
\end{gathered}

Where we have approximated the concentration gradient as being linear.

Diffusion coefficient

Diffusion is a thermally-activated process, and the temperature dependence is reflected in the diffusion coefficient. The diffusion coefficient (diffusivity) is also described by an Arrhenius relationship! Picture an atom diffusing through a crystalline solid: it has to move through the lattice. One way this can happen is, if the atom is sufficiently small, it can travel hop from interstitial site to interstitial site. Larger atoms can diffuse, too, but it’s a more energy-consuming process. One mechanism for this to happen is if a vacancy is first created in the lattice, and then the diffusing atom moves into the now-vacant lattice site. As vacancies diffuse through the lattice, other species can follow. Of course, there are more moving parts with this process, and more energy is required.

The energy required for diffusion to occur can be thought of as an activation energy. The diffusion coefficient is

\(D=D_0 e^{-\dfrac{E_a}{k_B T}}\)

Here, \(D_0\) is the maximum value of diffusivity, \(E_a\) is the activation energy, \(k_B\) is the Boltzmann constant, and \(T\) is temperature. By describing the diffusion coefficient with an Arrhenius relation, recall that we are saying that at a given temperature, \(T\), the ratio of the thermal energy given by \(k_B T\) to the activation energy \(E_a\) sets the value of the diffusion coefficient, and it is maximized at infinite temperature.

Fick’s second law

If the concentration profile varies with respect to time, the steady-state assumption no longer holds, and instead Fick’s second law is used instead:

\(\dfrac{\partial C}{\partial t}=D \dfrac{\partial^2 C}{\partial x^2}\)

Solutions to Fick’s second law are of the form

\(\dfrac{C(x, t)-C_0}{C_s-C_0}=1-\operatorname{erf}\left(\dfrac{x}{2 \sqrt{D t}}\right)\)

Here, \(C_s\) is the concentration of the source, \(C_0\) is the initial concentration, \(C(x, t)\) is the expression for concentration as a function of position and time, \(\mathrm{D}\) is the diffusion coefficient, and erf is the error function.