6.13: Bravais Lattices and Crystal Packing

Bravais lattices

To describe a crystal you need two ingredients: a lattice and a basis. Put another way, the lattice describes how atoms are arranged spatially: in a crystal, it is a regular, ordered pattern that tiles 3D space. The basis is the unit that is copied over the pattern: it usually consists of one or more atoms. Crystallographers utilize a set of patters called Bravais lattices to describe the ways atoms can be arranged to form crystalline solids. In \(3.091\), we will focus on the subset of the Bravais lattices that are cubic: the scale in all three dimensions is the same.

There are three cubic lattices: simple cubic (SC), body-centered cubic (BCC), and face-centered cubic (FCC).

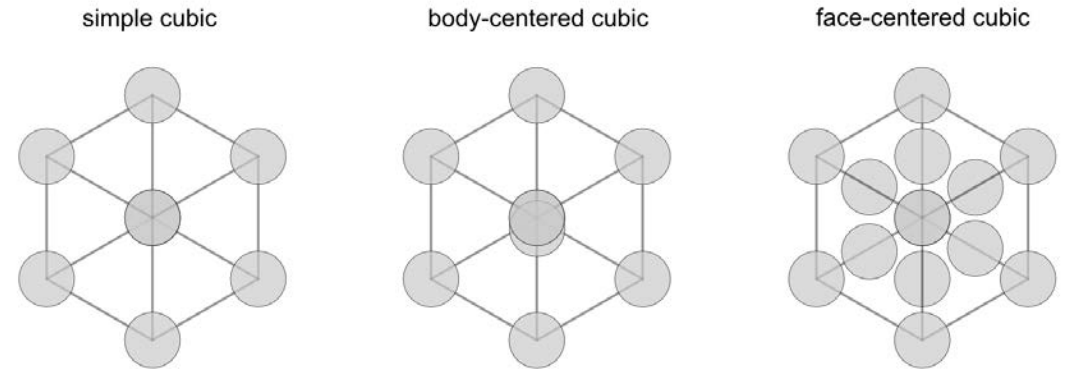
In the figure above, the grey grid shows the outline of the unit cell, while each circle represents an atom. For the atoms along the corners of the unit cell, each atom is shared amongst eight neighboring cells, so each cell contains \(1 / 8\) of an atom. Similarly, each of the face atoms in the FCC unit cell are shared between two cells, so each contains \(1 / 2\) an atom. We can calculate how many atoms are in each of the cubic unit cells:

\(N_{S C}=8\) corners \(* \dfrac{1}{8}\) atoms per corner \(=1\) atom per \(\mathrm{SC}\) unit cell

\(N_{B C C}=8\) corners \(* \dfrac{1}{8}\) atoms per corner \(+1\) central atom \(=2\) atoms per BCC unit cell

\(N_{F C C}=8\) corners \(* \dfrac{1}{8}\) atoms per corner \(+6\) face atoms \(* \dfrac{1}{2}\) atoms per face \(=4\) atom per \(\mathrm{FCC}\) unit cell

Crystal packing

We can now define some relevant metrics to describe the atomic density in different lattices and even along different directions within the crystal. We will talk about density both in terms of area and volume. To define a few terms:

• packing density: ratio of space occupied by atoms to total space available. Units are \(\left[\frac{\text { atoms }}{n m^2}\right]\) (by area) or \(\left[\frac{\text { atoms }}{n m^3}\right]\) by volume
• atomic packing factor: fraction of space occupied by atoms, in 2D (area ratio) or 3D (volume ratio). It is a unitless value between 0 and 1.

We also need to remember a few things from geometry: the area of a circle is \(\pi r^2\), and the volume of a sphere is \(\frac{4}{3} \pi r^3\). For a cubic system with side length \(a\) has face diagonal length \(\sqrt{2} * a\) and body diagonal length \(\sqrt{3} * a\). The trick to successfully solving packing questions is being able to relate the radius of the atoms (assuming they are hard spheres and as close packed as possible) and the side length of the unit cell. From there, it's just a bit of algebra to find the solution.

Example: Below is a section of an FCC unit cell: it is a cut-away of one face. First, find the relationship between the radius of the atoms, \(r\), and the unit cell width, \(a\). Then, determine how many atoms are in the \(2 \mathrm{D}\) unit cell. Finally, calculate the packing density of this plane (assuming \(a=3.5 \AA\) ), and the 2D atomic packing fraction.

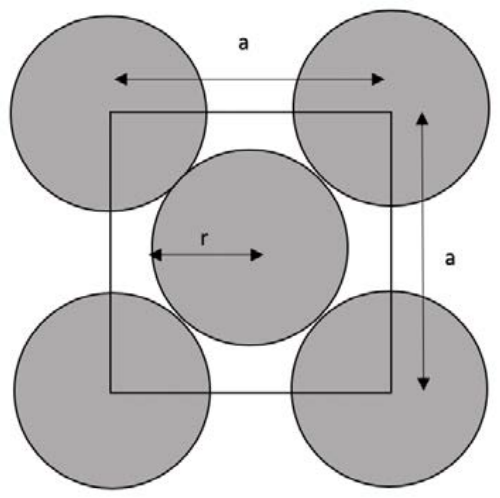
Answer

First, we need to relate \(r\) to \(a\). The easiest way to do this is usually to look along the closest packed direction: here, if we go down a diagonal, the atoms are always in contact along their center.

\[r+2 r+r=\sqrt{2} * a \nonumber\]

\[r=\dfrac{\sqrt{2}}{4} a \nonumber\]

Then, we want to figure out how many atoms are enclosed in the square, \(2 \mathrm{~d}\) unit cell. There is one full atom in the middle, and four corners which each contain \(1 / 4\) of an atom.

4 corners \(* \dfrac{1}{4}\) atoms per corner \(+1\) center atom \(=2\) atoms per unit cell

The packing density in two dimensions is the number of atoms per square nm. We can simply divide the number of atoms in the unit cell by the area of the unit cell:

\[\text { packing density }=\dfrac{2 \text { atoms per unit cell }}{(3.5 \AA)^2 \text { per unit cell }}\left(\dfrac{100 \AA^2}{1 \mathrm{~nm}^2}\right) \approx 16.33 \text { atoms } / \mathrm{nm}^2 \nonumber\]

The packing fraction in two dimensions is the fraction of space occupied by atoms:

\begin{gathered}
\text { packing fraction }=\frac{\text { area occupied by atoms }}{\text { total area }}=2[\text { atoms } / \text { unit cell }] *\left(\frac{\pi r^2[\text { area per atom] }}{a^2[\text { area per unit cell }]}\right) \\
=\frac{2 \pi *\left(\frac{\sqrt{2}}{4} a\right)^2}{a^2}=\frac{\pi}{4}=0.7854
\end{gathered}