4.3: Exam 3

Problem 1 (23 POINTS)

a) In the 2 crystalline solids shown below, there are circled SIX different point defects TOTAL. Label each defect with its name. (6 points)

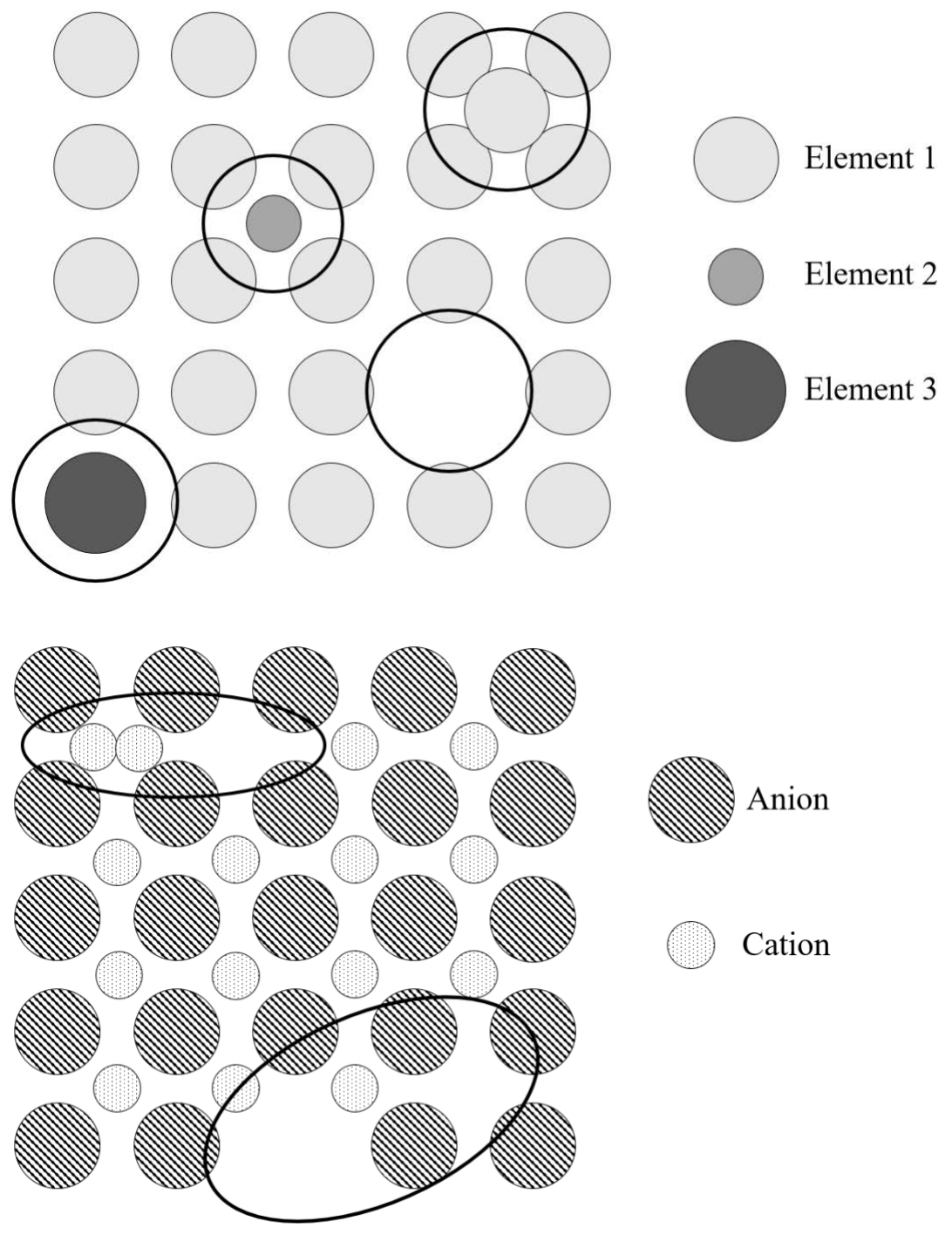
You decide to buy a ring from a jewelry store down on Mass Ave. Drawing on your deep knowledge of materials science from 3.091, you decide that a platinum ring is definitely the way to go. Unfortunately, the jeweler graduated from That School Down the Street; you are upset by their claim that the ring is “defect-free crystalline platinum.” Let’s prove them wrong!

b) First, you weigh the ring: it’s exactly 2 grams. How many platinum atoms are in the ring? (2 points)

c) How many atomic sites are in the ring, \(\mathrm{N}_{\mathrm{Pt}}\)? (2 points)

d) It's a little chilly in the shop: \(11^{\circ} \mathrm{C}(284 \mathrm{~K})\). Assuming the ring is in thermal equilibrium, calculate the total number of vacancies, \(\mathrm{N}_{\mathrm{v}}\), that you would expect at the current temperature. The constant, \(A\), has a value of 1.11. Assume the vacancy formation energy for \(\mathrm{Pt}\) is \(0.96 \mathrm{eV}\). (4 points)

e) The jeweler is stressed out by your frantic calculations and eager to prove they’re not cheating you; they hastily point out that the atoms that came from those vacancies are probably sitting in interstitial sites in the lattice. You quickly pull up a paper that has measured interstitial concentration in \(\mathrm{Pt}\).

Note: the units of interstitial defect concentration are mol/L.

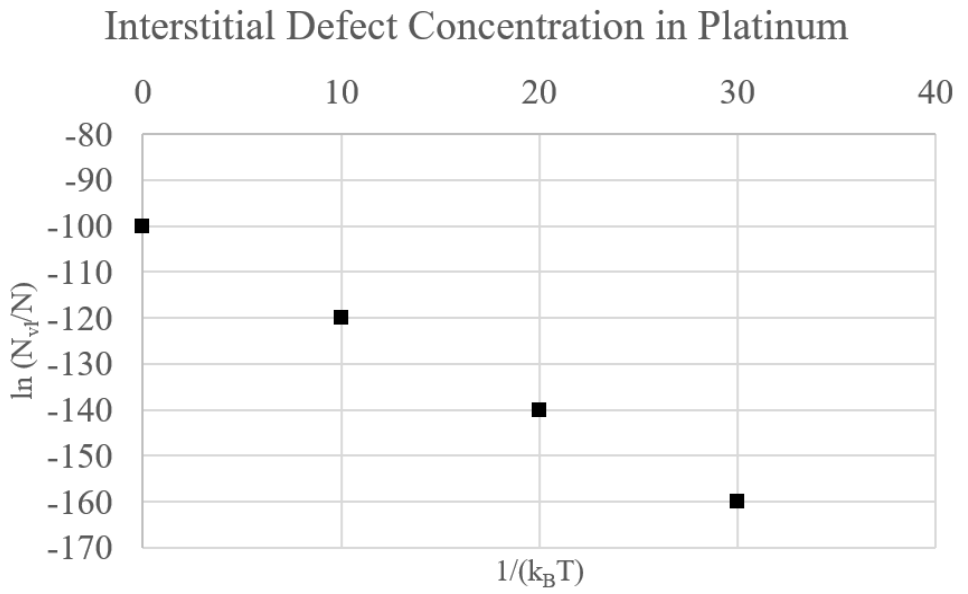
i) Estimate the formation energy (in J) of an interstitial defect from the plot. How does this compare to the vacancy formation energy in \(\mathrm{Pt}\), which was given above as \(0.96 \mathrm{eV}\)? Hint: assume that interstitial defect concentration follows an Arrhenius relationship. (5 points)

ii) Could the jeweler be right, based on the activation energies for interstitial formation and vacancy formation? In other words, could the atoms from the vacant sites have become interstitial defects? Explain your reasoning in one sentence. (4 points)

Problem 2 (20 POINTS)

a) Sketch the following on the axes provided:

i) A cooling curve (molar volume vs. temperature) for amorphous \(\mathrm{SiO}_2\) (3 points)

ii) A cooling curve (molar volume vs. temperature) for crystalline \(\mathrm{SiO}_2\) (3 points)

Please label curves \(\mathrm{i}\) and \(\mathrm{ii}\).

b) On your plot above, label:

i) the melting point(s) (2 points)

ii) the glass transition temperature(s) (2 points)

c) List TWO ways you could change the glass transition temperature. (4 points)

d) Tempered glass exhibits increased strength compared to regular glass. Consider a slice taken across a sheet of tempered glass:

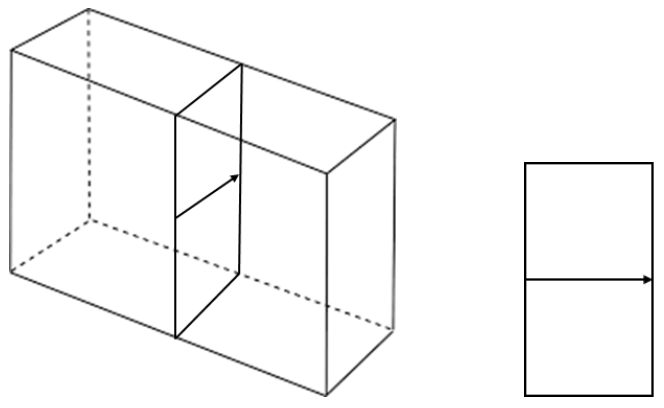
With reference to your plot in a), explain how the molar volume changes across the slice. (4 points)

e) Which of the following stress-strain curves could correspond to the tempered glass above? Circle the letter corresponding to your chosen curve. (2 points)

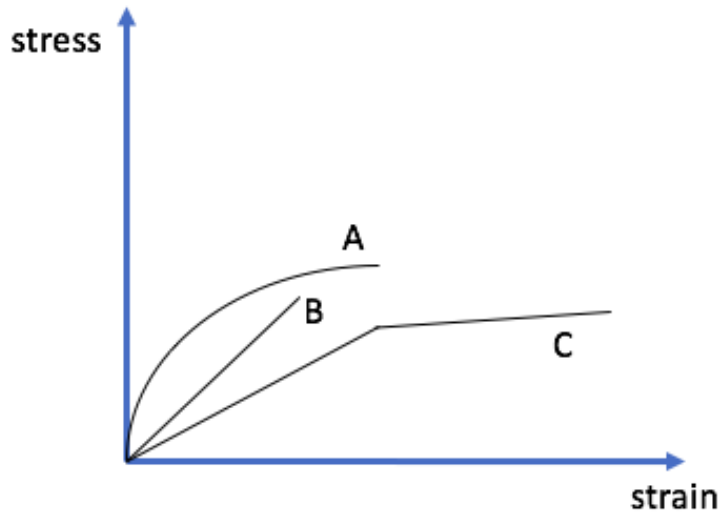
Problem 3 (20 POINTS)

In GB8, we explored the impact of ocean acidification on pteropods by considering the dissolution of \(\mathrm{CaCO}_3\) in a citric acid solution. Now, we'll consider a similar process, but using hydrofluoric acid instead. Hydrofluoric acid, \(\mathrm{HF}\), has a higher acid dissociation constant than citric acid.

a) Write out the acid dissociation reaction for hydrofluoric acid. Label the conjugate acid/base pairs. (5 points)

b) What is the concentration (M) of a solution containing \(0.05 \mathrm{~g}\) of \(\mathrm{HF}\) in \(0.1 \mathrm{~L} \mathrm{H}_2 \mathrm{O}\)? (3 points)

c) If the acid dissociation constant for hydrofluoric acid is \(\mathrm{K}_{\mathrm{a}}=7.2 \times 10^{-4}\), what is the \(\mathrm{pH}\) of the solution from part b)? (4 points)

e) If we had given you hydrofluoric acid \(\left(\mathrm{K}_{\mathrm{a}}=7.2 \times 10^{-4}\right)\) rather than citric acid \(\left(\mathrm{K}_{\mathrm{a}}=1.8 \times 10^{-5}\right)\) in the goodie bag, would you expect the shells to have dissolved faster or slower? Briefly explain why. (4 points)

f) Explain what would happen to the \(\mathrm{pH}\) of the hydrofluoric acid solution if it were to sit in a \(\mathrm{CO}_2\) environment for a few hours, and why. (4 points)

Problem 4 (21 POINTS)

To compensate for some of the oxygen consumed by burning the candle on one of your many Friday night dates, you decide to run a reaction that produces \(\mathrm{O}_2\) gas as fast as possible. You recall two options:

\((p) 2 \mathrm{NO}_2 \rightarrow 2 \mathrm{NO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \quad \mathrm{OR} \quad (q) \mathrm{O}_3+\mathrm{Cl} \rightarrow \mathrm{ClO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g})\)

You are able to find some information about the reaction \((p)\) : its rate law is

\(\text { rate }=\mathrm{k}\left[\mathrm{NO}_2\right]\)

(Note: reactions \(p\) and \(q\) have the same numerical value for their reaction constants)

Trial #	[\(\mathrm{O}_3\)] \(\mathrm{M}\)	[\(\mathrm{Cl}\)] \(\mathrm{M}\)	rate \(\mathrm{M}/\mathrm{s}\)
1	0.07	0.25	10
2	0.14	0.25	20
3	0.07	0.5	20

a) Use the experimental data in the table above about reaction (\(q\)) to determine its:

i. Rate law (5 points)

ii. Overall order (2 points)

iii. Value of \(\mathrm{k}\), the reaction constant (5 points)

b) Plot the linear version of the integrated rate law that describes \(2 \mathrm{NO}_2 \rightarrow 2 \mathrm{NO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g})\). Label the axes, \(y\)-intercept, and slope. (5 points)

c) If you have 2 mols of \(\mathrm{NO}_2, 1 \mathrm{~mol} \mathrm{of} \mathrm{Cl}\), and \(1 \mathrm{~mol}\) of \(\mathrm{O}_3\) available (but you can only run one reaction), which reaction would you choose to produce oxygen the fastest? Justify your answer with ONE sentence. (4 points)

Problem 5 (16 POINTS)

Your research supervisor wants you to characterize two pure elemental powders she found in the back of the lab. Unfortunately, time on the XRD machine is very limited; to save time, you mix BOTH POWDERS together and perform XRD on the mixture.

You get the following plot of intensity (counts) vs. \(2 \theta\) (degrees):

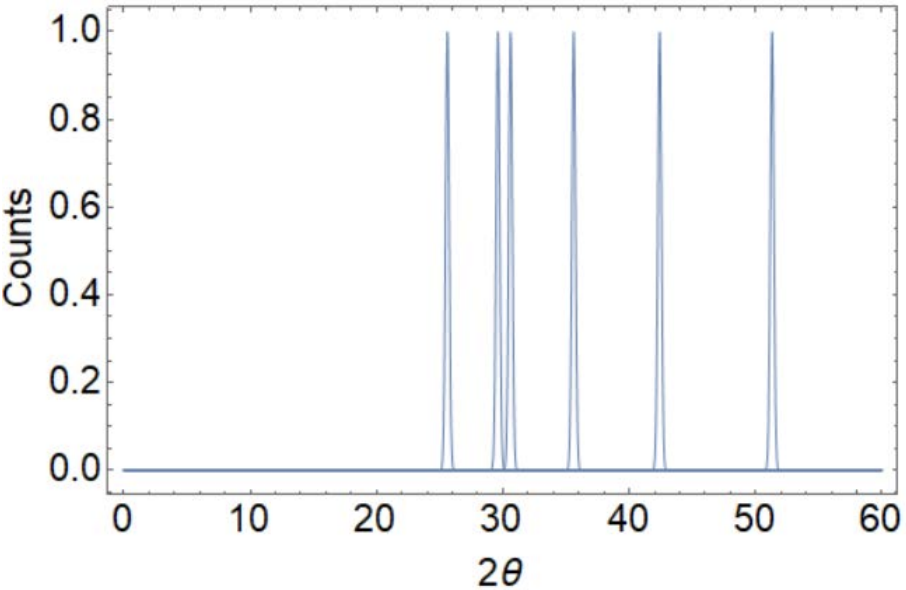
From the plot, you have the following data to help identify the samples. You may find it helpful to add columns to assist your thinking (ungraded).

\(2 \theta\) (degrees)	\((\sin \theta)^2\)
25.6	0.049
29.6	0.065
30.7	0.070
35.6	0.093
42.4	0.131
51.3	0.187

a) Use selection rules to determine the crystal structures of the samples (8 points) Note: Assume sample 1 corresponds to the element with the lowest 2-theta peak.

 

Sample 1: ___________________________                                                                                                             Sample 2: ___________________________

b) What are the lattice constants of the samples? Copper k-alpha radiation (wavelength=1.54 Angstroms) was used. Show your thinking! (8 points)

Sample 1: ___________________________                                                                                                             Sample 2: ___________________________