4.2: Exam 2

Problem 1 (17 POINTS)

a. Use the fact that \(\mathrm{SeOF}_2\) is trigonal pyramidal to write the Lewis Dot Structure, including lone pairs, for \(\mathrm{SeOF}_2\). (3 points)

b. Below is a drawing of two different amino acids, Methionine and Lysine, without any lone pairs drawn.

Name the VSEPR geometry around the following central atoms:

i.The sulfur in methionine (2 points)

ii.The circled carbon in lysine. (2 points)

iii.Which of these angles is smaller? Explain why or why not in ONE sentence. (2 points)

\[\mathrm{CH}_2-\mathrm{S}-\mathrm{CH}_2 \quad \mathrm{OR} \quad \mathrm{CH}_2-\mathrm{CH}_2-\mathrm{CH}_2 \nonumber\]

c. Below is one structure for the molecule \(\left[\mathrm{CH}_6 \mathrm{~N}_3\right]^{+}\)

i. There are three other resonant structures for this molecule; what are they? (6 points)

ii. The structure that we gave you for \(\left[\mathrm{CH}_6 \mathrm{~N}_3\right]^{+}\) contributes the least to the overall bonding of the molecule (it is the least stable). Why? (2 points)

Problem 2 (23 POINTS)

\(\mathrm{NaCl}\) is a compound that forms a rock salt structure (unit cell below). The radius of the \(\mathrm{Na}^{+}\) atoms is \(1.16 \AA\); the radius of the \(\mathrm{Cl}^{-}\) atoms is \(1.67 \AA\left(1 \AA=10^{-10} \mathrm{~m}\right)\).

a. Name the Bravais lattice (lattice type) of \(\mathrm{NaCl}\). What is the basis? (2 points)

b. How many \(\mathrm{Na}^{+}\) ions are in the unit cell? How many \(\mathrm{Cl}^{-}\) ions? (4 points)

c. Determine the close-packed direction of this structure and use it to calculate the lattice parameter, a. ( 3 points)

d. Draw (211), [0\(\bar{2}\)1], [301], and (1\(\bar{1}\)0) in the boxes below. Make sure to label which is which. (8 points)

e. Which of the planes in part d is closer in distance to its equivalent plane in a neighboring cell? Show how you arrived at this answer. (4 points)

f. Using atomic packing factor, explain why calcium is denser than potassium. (2 points)

Problem 3 (18 POINTS)

a. Rank the following intermolecular forces in terms of their average relative strength: London dispersion, hydrogen bonding, dipole-dipole, and dipole-induced-dipole. (4 points)

1. ___________________ (strongest)

2. ___________________

3. ___________________

4. ___________________ (weakest)

You have the four following molecules in liquid form in your lab cabinet.

b. Which has the highest boiling point? (2 points)

c. You make a mixture of two of the liquids.

i. If you wanted your mixture to have the LOWEST possible boiling point, which two of the four molecules would you choose? (4 points)

ii. If you want your mixture to have the HIGHEST possible boiling point, which two of the four molecules would you choose? (4 points)

d. You have two samples of polyethylene, a polymer made of chains of carbon and hydrogen, as shown below. For one sample, each molecule chain is 50 units long and in the next sample, each chain is 500 units long. Which sample of plastic will be stronger? Why? (4 points)

Problem 4 (21 POINTS)

a. The molecular orbitals of a second-row diatomic molecule are shown in this figure. Label them each as \(\sigma, \sigma^*, \pi\), or \(\pi^*\) by filling in the boxes provided. (The \(2 \mathrm{p}\) and \(2 \mathrm{~s}\) atomic orbitals are labelled for reference). (6 points)

b. Circle which of the following this skeleton MO diagram could correspond to. (2 points)

\(\mathrm{C} - \mathrm{C}\)                                         \(\mathrm{N} - \mathrm{O}\)                                        \(\mathrm{H} - \mathrm{F}\)

c. Rank the following molecules in terms of stability: \(\mathrm{Li}_2, \mathrm{Be}_2 \mathrm{~B}_2, \mathrm{C}_2\) Be sure to show your work (no need to show MO diagrams). (8 points)

d. Acrylonitrile is a feedstock chemical used for the manufacture of “nitrile” polymers. Pictured below is its chemical structure. What is the hybridization of the circled atoms? (3 points)

d. Give the total number of \(\sigma\) bonds and total number of \(\pi\) bonds in acrylonitrile. ( 2 points )

Problem 5 (21 POINTS)

a. UV light corresponds to wavelengths from \(10-400 \mathrm{~nm}\). What is the range of band gaps corresponding to UV light? (3 points)

b. You only have two materials in the lab to build an LED: GaAs (band gap \(1.42 \mathrm{eV}\) at \(300 \mathrm{~K}\)) and \(\mathrm{GaN}\) (band gap \(3.2 \mathrm{eV}\) at \(300 \mathrm{~K}\) ). Which would you choose as a UV emitter? (3 points)

c. UV light can damage eyes, so you decide that for safety, your LED should emit in the visible range too. You recall that you can tune the band gap by alloying your material. Determine the fraction \(\mathrm{x}\) of GaAs in your alloy such that \(\mathrm{GaA} \mathrm{s}_{\mathrm{x}} \mathrm{N}_{1-\mathrm{x}}\) will emit red light (wavelength \(700 \mathrm{~nm}\) ). Remember that the band gap of an alloy is the weighted average of the band gaps of its components. (3 points)

d. If you place the \(\mathrm{GaAs}_{\mathrm{x}} \mathrm{N}_{1-\mathrm{x}}\) adjacent to your answer from (B) your LED will emit both UV light and red light. However, you observe that it is really dim: you decide to dope it with \(\mathrm{Mg}\).

i. Is \(\mathrm{Mg}\) an \(\mathrm{n}\) - or \(\mathrm{p}\)-type dopant in \(\mathrm{GaAs}_{\mathrm{x}} \mathrm{N}_{1-\mathrm{x}}\)? (2 points)

ii. If you dope \(1 \mathrm{~g} \mathrm{GaN}\) with \(\mathrm{Mg}\) such that \(1 \mathrm{Mg}\) atom replaces 1 in every \(10^6 \mathrm{Ga}\) atoms, how many extra carriers are produced? What kind of carriers are these? (4 points)

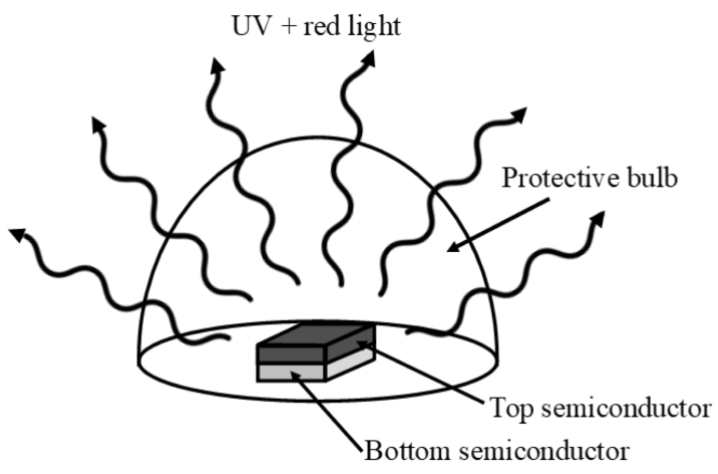
e. In order to get enough current to \(\mathrm{GaAs}_{\mathrm{x}} \mathrm{N}_{1-\mathrm{x}}\) and your answer from (B) processing requires that the two are stacked. Which should be on top to ensure no light is blocked? (3 points)

f. Do you expect a larger temperature-dependence of conductivity in the doped or the undoped \(\mathrm{GaAsN}\), at moderate temperatures? (3 points)