4.4: Final Exam

Problem 1 (21 POINTS)

a) i. Fill in atomic and Molecular orbitals for the \(\mathrm{MO}\) diagram of Carbon Monoxide (\(\mathrm{CO}\)) below (3 pts):

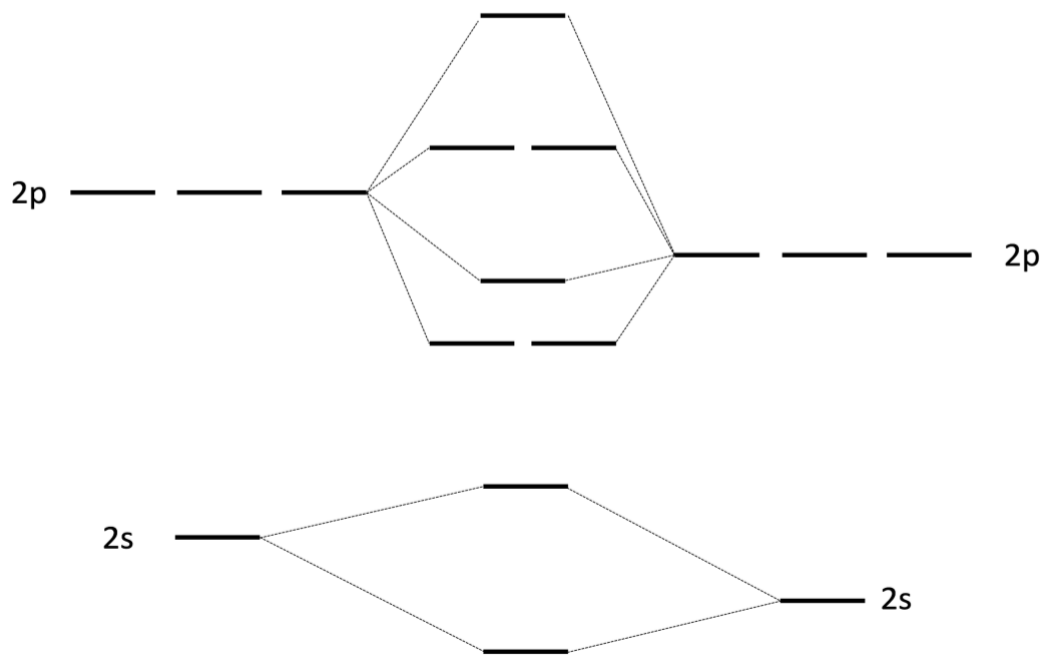
ii. Label the molecular orbitals as sigma or pi (2 pts)

iii. Label the molecular orbitals as bonding or antibonding (2 pts)

iv. What is the bond order of \(\mathrm{CO}\)? (2 pts)

b) Methylamine \(\left(\mathrm{H}_3 \mathrm{C}-\mathrm{NH}_2\right)\) is an organic compound that's used to synthesize lots of chemicals, ranging from photographic developers to cold medicine.

i. Draw a methylamine molecule, showing its 3D VSEPR geometry. Include any lone pairs. ( 3 pts)

ii. What is the shape predicted by VSEPR of the atoms around (2 pts) ...

\(\mathrm{C}\):_____________________                                                                                                       \(\mathrm{N}\):____________________

iii. Consider the two bond angles in methylamine below. Which is larger? (1 pt)

1) \(\mathrm{H}-\mathrm{C}-\mathrm{N}\)
2) \(\mathrm{C}-\mathrm{N}-\mathrm{H}\)

                                                \(\overline{\text { Smaller }} \quad \quad \quad \overline{\text { Larger }}\)

c) If we add an \(\mathrm{H}^{+}\) ion to methylamine, we get methylammonium \(\left(\mathrm{CH}_3 \mathrm{NH}_3^{+}\right)\), an organic ion often used in perovskite solar cells.

i. Draw a methylammonium ion using its VSEPR geometry. Include any lone pairs. (2 pt)

ii. Label the formal charges on each atom on your drawing above (2 pts)

iii. Does methylammonium have any stable resonance structures? If so, draw one. If not, why not? (2 pts)

Problem 2 (17 POINTS)

You are a new scientist at a fancy spacesuit company. To test your polymer knowledge, your boss has asked you to design a material for their newest spacesuit. Unfortunately, in spite of the critical nature of the spacesuit, the chemistry lab seems to be horribly underfunded, and you have only two polymers to choose from.

a) Polymer 1 is made from the monomer tetrafluoroethylene \(\left(\mathrm{C}_2 \mathrm{~F}_4\right)\). Draw the Lewis Structure for a single tetrafluoroethylene molecule. What is the hybridization of one of the carbon atoms? (4 pts)

b) Draw the repeat unit for a polymer made from polymerization of this monomer. What polymerization technique should you use? (3 pts)

c) Polymer 2 is a polymer made from the following monomers. Draw the corresponding polymer. What polymerization technique should you use? (5 pts)

d) The space suits must deflect water, i.e. the polymer shouldn't interact with \(\mathrm{H}_2 \mathrm{O}\). Which polymer should you choose? (Polymer 1 or 2 ) Give a one-sentence explanation making sure to include intermolecular forces. ( \(3 \mathrm{pts})\)

e) Your boss is worried that your space suit will tear too easily. How could you modify your polymer to improve its durability? (2 pts)

Problem 3 (21 POINTS)

3. Iron (\(\mathrm{Fe}\)), which is an important component of many parts on the Apollo 3.091, forms a BCC structure at room temperature.

a) Draw the (110) plane of \(\mathrm{Fe}\) on the graph provided below. (3 pts)

Modified image of astronaut working. Original image is in the public domain (source: NASA).

        

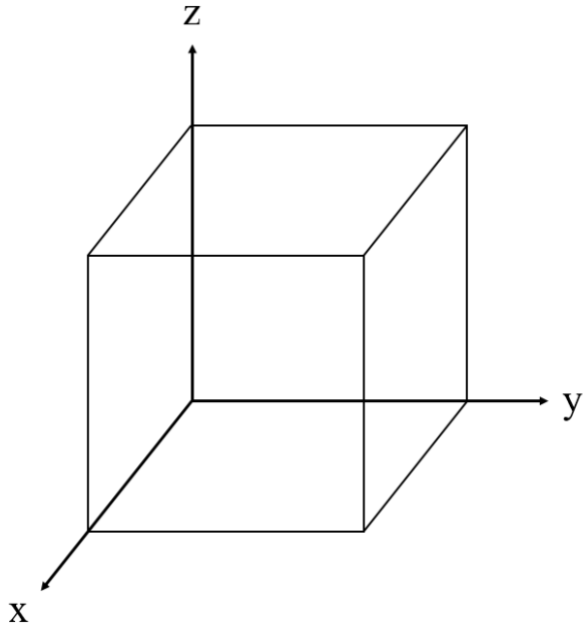
b) What is the close-packed direction of \(\mathrm{Fe}\)? Indicate where this is in relation to the (110) plane drawn above by DRAWING it on the graph provided in part (a) and LABEL the direction with the correct crystallographic nomenclature, \(<h k l>\). (5 pts)

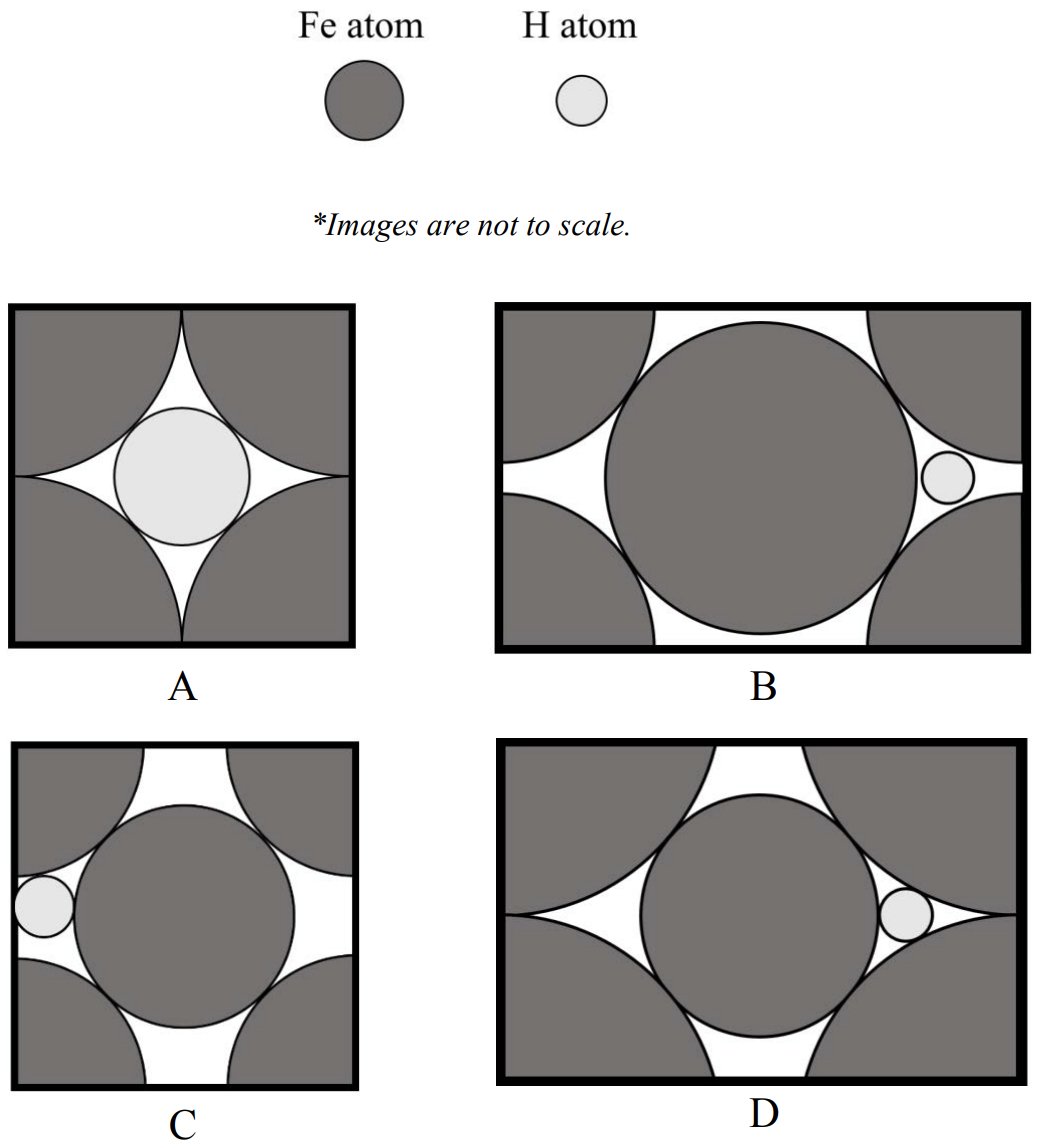
c) It is difficult to get 100% pure iron because there are often some impurity elements in the material. One common impurity element is hydrogen, which is present as an interstitial element in iron.

CIRCLE the image below that accurately shows an interstitial hydrogen atom in the (110) plane of iron. (3 pts)

d) Iron has a radius of \(1.24 \AA\). Calculate the density of \(\mathrm{Fe}\) in \(\mathrm{g} / \mathrm{cm}^3\)? ( 1 atomic mass unit \(= 1.66 \times 10^{-24}\) grams, \(\left.1 \AA=10^{-8} \mathrm{~cm}\right)(6 \mathrm{pts})\)

 

You decide to run a tensile test on an \(\mathrm{Fe}\) wire. After the experiment, you look at the part of the sample that has deformed and see the following:

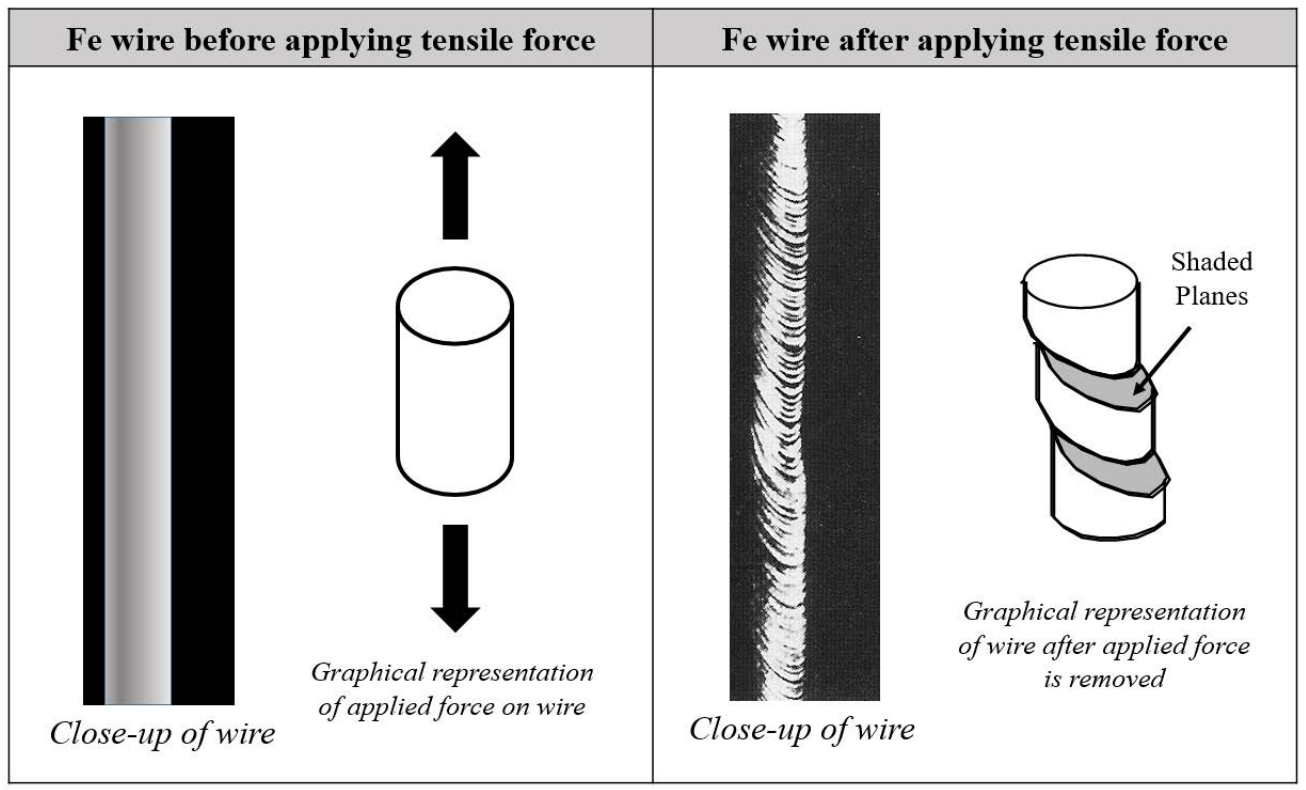
e) In ONE sentence, explain what is special about the shaded planes in the diagram above. (4 pts)

Problem 4 (20 POINTS)

We’ve talked a lot about semiconductors, but we haven’t mentioned one interesting class of semiconductors - organic semiconductors. Professor Grossman will be using organic LEDs for horticultural lighting on the spaceship, so it’s important to understand them!

LEDs can be used to grow plants in space!

a) One example of an organic semiconductor is polyethyne (\(\mathrm{PE}\)). A portion of its structure is shown below. Circle the repeating unit. (2 pts)

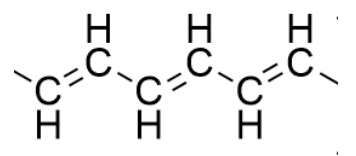
b) Polyethyne is a semiconductor because its resonance structures allow electrons to move. One is structure shown above; draw one repeating unit of another polyethyne resonance structure. (3pts)

c) To enhance conductivity to useful levels, polyethyne needs to be doped — but the dopants behave differently from inorganic semiconductors. When doping with bromine, two electrons are removed from the polymer per bromine molecule:

\[\mathrm{PE}+\mathrm{Br}_2 \rightarrow(\mathrm{PE})^{2+}+2 \mathrm{Br}^{-} \nonumber\]

In this case, is bromine acting as a \(\mathrm{p}\)-type dopant or \(\mathrm{n}\)-type? Briefly explain your answer. (Conduction occurs through the polymer chains; the bromine ions do not contribute significantly, and for this question you can assume that they are present only to keep total charge neutral) \((3 \mathrm{pts})\)

 

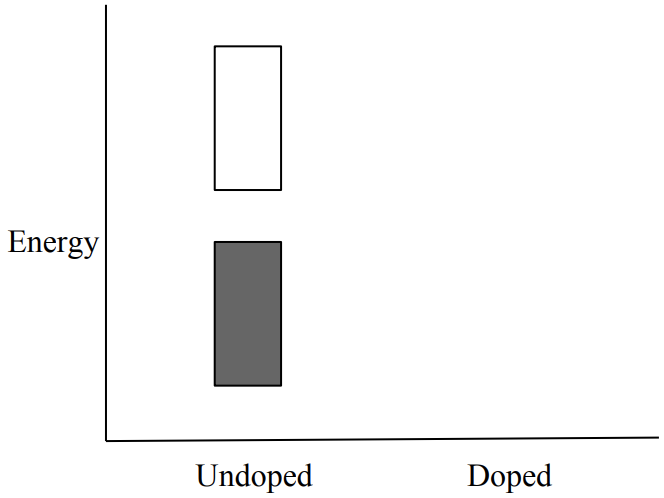
d) The band diagram for neutral polyethyne is shown below. Sketch the band diagram for \(\mathrm{Br}_2-\) doped polyethyne on the same axes. (4 pts)

e) Certain organic semiconductors follow the same trend of temperature vs. conductivity as inorganic semiconductors. A schematic is shown below.

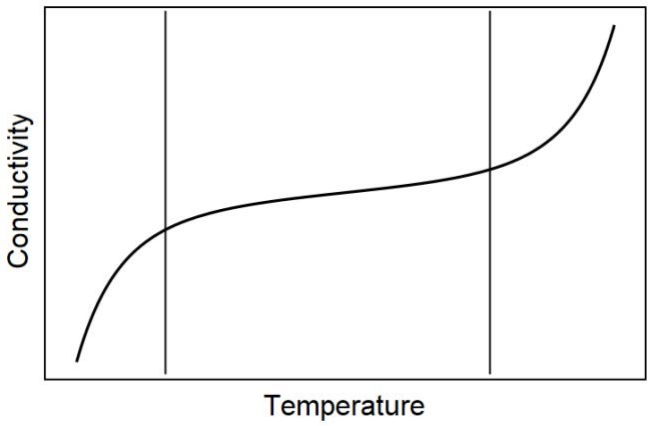
i. What causes the near-zero slope of temperature dependence in the intermediate temperature regime? (4 pts)

ii. Theoretical studies have shown that polyethyne could exhibit near-zero temperature dependence from 100 \(\mathrm{K}\) up to about 450 \(\mathrm{K}\); however, the glass transition temperature of your PE is near 400 \(\mathrm{K}\). What is one thing you could do to increase the glass transition temperature of your PE semiconductor so that it can be used over a wider temperature range? (4 pts)

Problem 5 (21 POINTS)

An alien sword of a PURE METAL has fallen from space onto MIT’s campus! As an expert materials scientist, you’re called in to investigate its properties.

An alien sword! Who knows what it’s made of… oh wait, we can find out using x-rays. :)

a) First thing’s first - let’s figure out what crystal structure the material in this sword has! You stick the sword into your x-ray diffraction (XRD) machine and wait for some results.

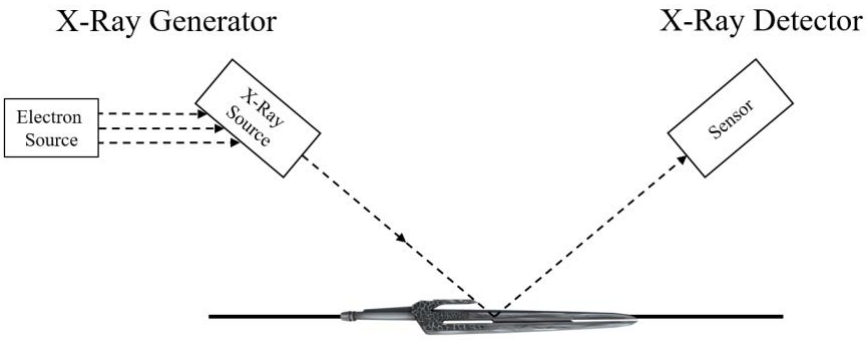
(Note: It’s a little different in real life.)

Unfortunately, the alien sword releases a blast of ~alien energy~ during the experiment! Not only does it damage your XRD machine, but your results get all ripped up. You manage to salvage some PIECES of the XRD graph, shown below:

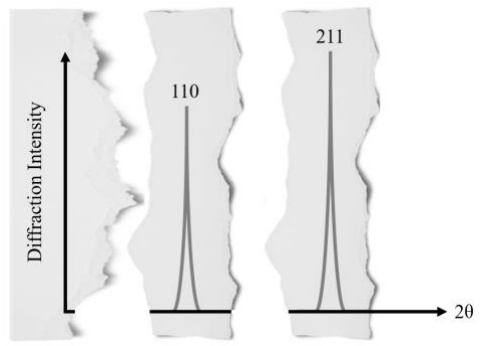
Based on the salvaged XRD graph, what are ALL of the possible cubic crystal structures the sword could have? (4 pts)

b) You still don’t know what the sword is made of! Luckily, the x-ray generator part of your million-dollar XRD machine hasn’t been damaged. Undeterred, you decide to make the sword the source of x-rays by accelerating electrons at it to generate an x-ray spectrum.

Draw an x-ray spectrum. Label the horizontal and vertical axes, the Brehmsstrahlung radiation, \(\mathrm{K}_\alpha, \mathrm{K}_\beta, \mathrm{L}_\alpha\), and \(\mathrm{L}_\beta\). (6 pts)

 

c) You can figure out what material your sword is by analyzing its x-ray spectrum!

In the resultant \(\mathrm{x}\)-ray emission spectrum, you observe a \(\mathrm{L}_\alpha\) peak at a wavelength \(\lambda=2.383 \times 10^{-9}\) meters. What is the metal the sword is made of? Assume the screening factor, sigma \((\sigma)\), for \(\mathrm{L} \alpha\) radiation is \(7.4\).

Use the equation \(E=13.6 *(Z-\sigma)^2\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)\), where \(\sigma\) is the screening factor. (3 pts)

 

d) Unfortunately, you got so absorbed in your work that you don’t notice shooting accelerated electrons at the sword has heated it up! The sword has been at 600\(\mathrm{K}\) for the 3 hours you spent analyzing your data. In other words, the sword has been ANNEALED.

In ONE sentence, explain how this might change at least two mechanical properties of the sword. (4 pts)

 

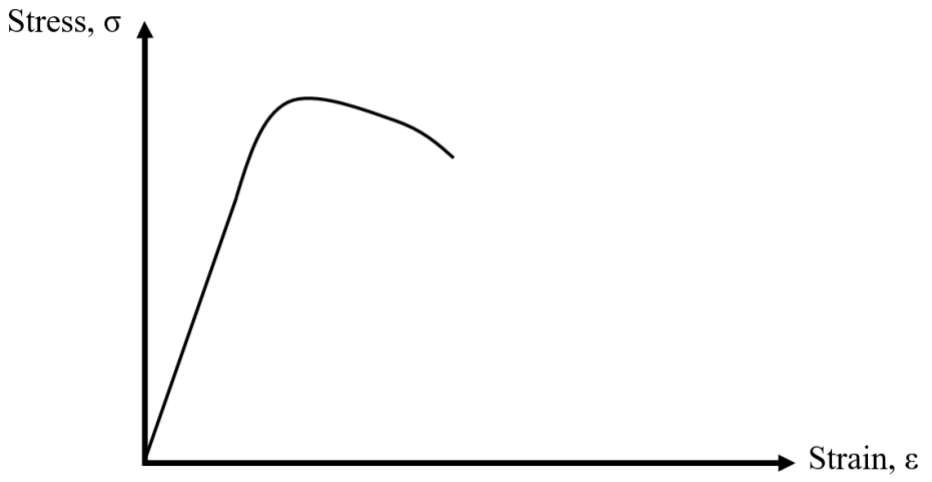
e) The graph below has a stress-strain curve for the sword BEFORE your experiments.

i. Draw the stress-strain curve for the sword AFTER your experiments, i.e. after it was ANNEALED and has been returned to room temperature. (4 pts)

Problem 6 (19 POINTS)

You're working in Professor Grossman's lab and have been given the following solutions:

Solution 1: \(0.0334\) grams of \(\mathrm{CaF}_2\) in \(2 \mathrm{~L}\) of water
Solution 2: \(0.0334\) grams of \(\mathrm{CaF}_2\) in \(3 \mathrm{~L}\) of water
Solution 3: Solution \(2+1 \mathrm{~L}\) of \(5^* 10^{-5} \mathrm{M} \mathrm{PbF}_2\)

a) Assuming the ionic solid completely dissolves to create a saturated aqueous solution, what is the \(\mathrm{K}_{\mathrm{sp}}\) of \(\mathrm{CaF}_2\) in Solution 1 ? (3 pts)

b) The concentration of Solution 2 is \(1.43^* 10^{-4} \mathrm{M}\), and the \(\mathrm{K}_{\mathrm{sp}}\) of \(\mathrm{PbF}_2\) is \(3.7^* 10^{-8}\).

i. What are the concentrations of each ion in Solution 3? (4 pts)

ii. Write out the \(\mathrm{K}_{\mathrm{sp}}\) expressions for both \(\mathrm{CaF}_2\) and \(\mathrm{PbF}_2\). (2 pts)

iii. Use the expressions from b)ii. to show why there wouldn't be any precipitates. (4 pts)

c) Now, consider Solution 2 alone. You want to precipitate the \(\mathrm{CaF}_2\) out of solution using one of the following chemicals in your lab: \(\mathrm{PbI}_2, \mathrm{CaS}\), and \(\mathrm{MgF}_2\).

i. Name one chemical you could use to precipitate \(\mathrm{CaF}_2\). (there may be multiple correct answers) ( 2 pts)

ii. How many moles of the chemical that you chose for part c) i. are necessary to precipitate the original \(4.28 * 10^{-4}\) moles of \(\mathrm{CaF}_2\) out of the solution? (4 pts)

PROBLEM 7 (25 POINTS)

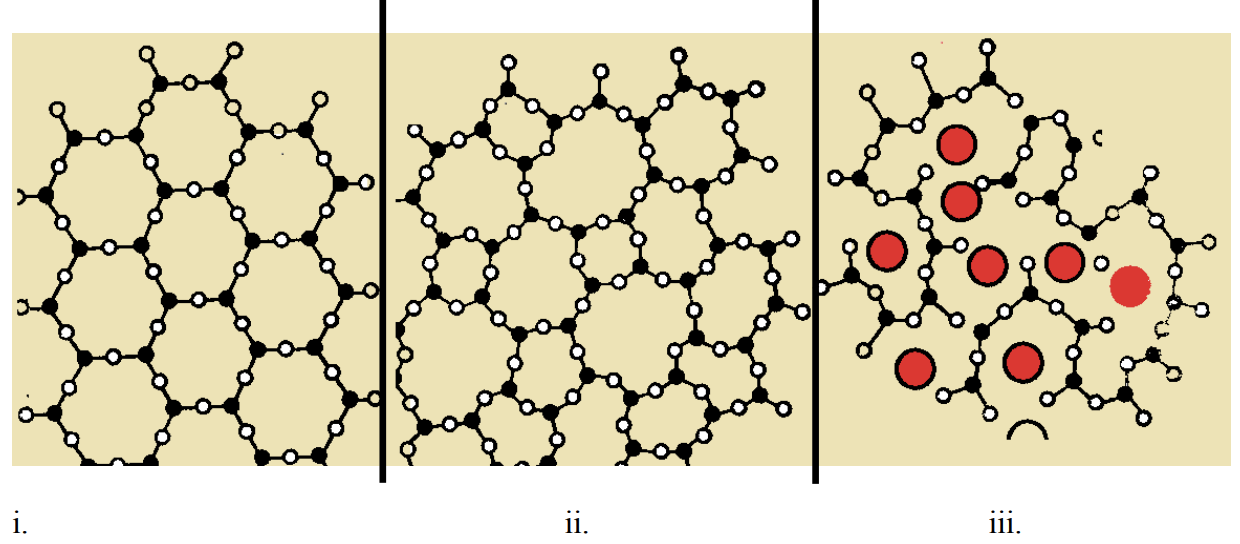
Above are sketches (from three different textbooks) of three samples of silicon dioxide. One of the samples contains \(\mathrm{Na}_2 \mathrm{O}\) as a network modifier.

a) Which sample contains \(\mathrm{Na}_2 \mathrm{O}\)? (2 pts)

b) Which sample is crystalline quartz? (2 pts)

c) Plot the molar volume vs temperature curves of the three materials on the same plot. Be sure to label your axes. (6 pts)

d) \(\mathrm{Na}_2 \mathrm{O}\) and \(\mathrm{CaO}\) are both network modifiers. Network modifiers are added when the glass is in a liquid state. You know that the rate law for the dissolution of \(\mathrm{CaO}\) in liquid silica is rate \(_{\mathrm{CaO}}=4[\mathrm{CaO}]\).

Write a similar rate law for the dissolution of \(\mathrm{Na}_2 \mathrm{O}\) in liquid silica and use it to fill in the following table. The \(\mathrm{Na}_2 \mathrm{O}\) reaction is second order in terms of \(\mathrm{Na}_2 \mathrm{O}\) and independent of the silica concentration. Please determine the value of the rate constant, and write the units for \(\left[\mathrm{Na}_2 \mathrm{O}\right]\) and rate.

Fill in the units row and find the rate of trial 2 \((8 \mathrm{pts})\):

	\(\left[\mathrm{Na}_2 \mathrm{O}\right]\)	rate
Unit
Trial 1	\(2 \times 10^{-5}\)	\(1.2 \times 10^{-9}\)
Trial 2	\(4 \times 10^{-5}\)

 

\(\text{Rate law:}\)                        \(\text{rate}_{\mathrm{Na}2\mathrm{O}}\) = ________________________

 

e) What are the units of the rate constant in:

i. the \(\mathrm{CaO}\) rate law ( \(\left.2 \mathrm{pts}\right)\)

ii. the \(\mathrm{Na}_2 \mathrm{O}\) rate law ( \(\left.2 \mathrm{pts}\right)\)

 

f) Thinking about the size of \(\mathrm{Na}\) vs. \(\mathrm{Ca}\) ions, explain in ONE sentence why it makes sense that the sodium oxide reaction occurs at a faster rate than the calcium oxide reaction. (3 pts)

Problem 8 (24 POINTS)

You’re interested in understanding the diffusion of hydrogen gas through a palladium (\(\mathrm{Pd}\)) filter to make sure the concentration of \(\mathrm{H}\) doesn’t get too high in the living quarters of the rocket.

Modified astronaut sleeping. Original image is in the public domain (source: NASA).

a) Calculate the original number of \(\mathrm{Pd}\) vacancies in a \(1 \mathrm{~mol}\) sample of \(\mathrm{Pd}\), assuming a vacancy activation energy \(=0.7 \mathrm{eV}, \mathrm{T}=300 \mathrm{~K}\), and the entropic constant \(\mathrm{A}=1(5 \mathrm{pts})\)

 

b) Does hydrogen diffuse through the palladium lattice through interstitial sites or through substitutional sites? Use Hume-Rothery rules to justify your answer in ONE sentence. ( 3 pts)

 

c) The diffusion coefficient of hydrogen through palladium at \(300 \mathrm{~K}\) is \(3.2 \times 10^{-10} \mathrm{~m}^2 / \mathrm{s}\). You expose one side of the wafer to a hydrogen atmosphere with concentration \(0.0446 \mathrm{M}\) and the other to air with a hydrogen concentration of \(2.23 \times 10^{-8} \mathrm{M}\). What is the flux of hydrogen atoms through this Pd crystal at \(300 \mathrm{~K}\)? The Pd wafer is \(2.7 \mathrm{~mm}\) thick. Hint: 1 liter is \(0.001 \mathrm{~m}^3\). (5 pts)

 

d) Draw the concentration profile of hydrogen atoms across this crystal at 300\(\mathrm{K}\). (3 pts)

e) At \(400 \mathrm{~K}\), the diffusion coefficient is \(\mathrm{D}(400 \mathrm{~K})=3.51 \times 10^{-5} \mathrm{~m}^2 / \mathrm{s}\).

i. Assume that diffusion follows the Arrhenius law: \(\mathrm{D}=\mathrm{D}_0 * \exp \left(-\mathrm{E}_{\mathrm{a}} /\left(\mathrm{k}_{\mathrm{B}} \mathrm{T}\right)\right)\). What is the activation energy \(\mathrm{E}_{\mathrm{a}}\) of the diffusion of \(\mathrm{H}\) through \(\mathrm{Pd}\)? (4 pts)

ii. At what temperature should we hold the Pd such that the flux of hydrogen atoms through the Pd filter is \(1.38 \times 10^{-4} \mathrm{~mol} / \mathrm{m}^2 \mathrm{~s}\)? Hint: use the information from part c. or part e. to determine \(\mathrm{D}_0\).(4 pts)

Problem 9 (19 POINTS)

The following diagram shows the pH of some common substances:

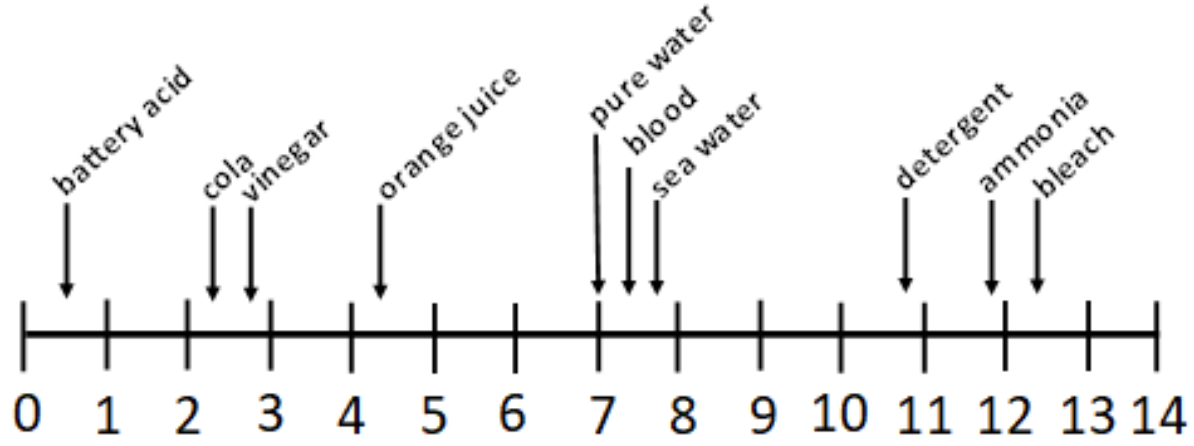
a) From the scale above, name:

i. The strongest acid (1 pt)

ii. The weakest base (1 pt)

iii. A neutral substance (1 pt)

The acidic ingredient in vinegar is acetic acid \(\left(\mathrm{CH}_3 \mathrm{COOH}\right)\). You bought a bottle of vinegar and measured the \(\mathrm{pH}\) of your solution is around \(2.4\), and the molar concentration of acetic acid in vinegar is around \(0.85 \mathrm{M}\).

 

b) Write the acid reaction of acetic acid with water. Label the conjugate acid and base pairs. (4 pts)

 

c) What is the hydronium ion \(\left(\mathrm{H}_3 \mathrm{O}^{+}\right)\) concentration of our \(0.85 \mathrm{M}\) solution of acetic acid? (3 pts)

 

d) Based on the information given and your answer to parts b) and c), determine the value of the acid ionization constant, \(\mathrm{K}_{\mathrm{a}}\), for acetic acid. (3 pts)

 

e) What is the hydronium ion \(\left(\mathrm{H}_3 \mathrm{O}^{+}\right)\) concentration of a \(0.010 \mathrm{M}\) solution of acetic acid? (3 pts)

 

f) What is the \(\mathrm{pH}\) of a \(0.010 \mathrm{M}\) solution of acetic acid? (3 pts)

 

Problem 10 (13 POINTS)

As the universe cooled after the big bang, ionized hydrogen \((\mathrm{H}+)\) combined with free electrons (\(\mathrm{e}-\)) to form hydrogen gas.

a) Write a balanced equation for this reaction. (2 pts)

 

b) When \(\mathrm{H}+\) and \(\mathrm{e}-\) combine, a photon is emitted as the electron relaxes to the ground state, essentially reversing the process of ionization from the ground state.

i. What is the energy of this electronic transition? (2 pts)

ii. What is the wavelength of the photon that is emitted? (3 pts)

 

c) We can learn about the elemental composition of stars by observing which wavelengths are absorbed by the star.

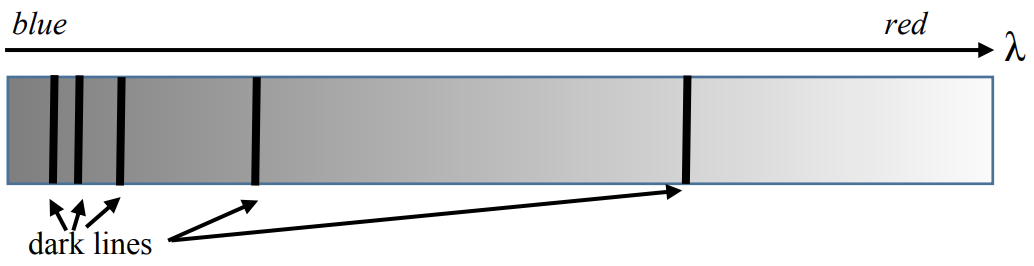
i. Explain in ONE sentence why absorption spectra have dark lines (as shown in the figure above). [Note – to save money at CopyTech we printed this in greyscale, but it was originally a spectrum going from blue to red.] (3pts)

ii. Explain in ONE sentence why the shorter-wavelength dark lines are closer together than the longer-wavelength dark lines (3pts)

Modified image of astronaut waving © original source unknown. All rights reserved. This content is excluded from our Creative Commons license. For information, see https://ocw.mit.edu/fairuse.