8.3: Physical properties
- Page ID
- 125422
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It is barely imaginable that materials based on the physical properties of solid inorganic compounds have played such decisive roles in present-day technology and industry. One may think that this field belongs more to material physics. However, apart from the theories of physical properties, the contribution of chemistry and chemists to the preparation of materials and their structural analysis has been greater than that of other branches of science. Material science is the application of the fundamental physical properties of materials such that basic theories and their applications converge. Therefore, by surveying the applications in such fields, the outlines of research themes and their purposes can be understood.
Important inorganic materials are surveyed from the chemical point of view by focusing on the relationship between preparation and isolation, and structure and physical properties.
(a) Electric properties
A semiconductor is an electrical conductor with electrical resistance in the range of about 104 to 108 ohms. A typical semiconductor is a super-high grade silicon that is manufactured on a large scale and is widely used for information processing devices such as computers and energy conversion devices such as solar cells. VLSI (very large-scale integrated circuits) are printed on wafers made from almost defectless silicon single crystals with diameters of no less than 20 cm, prepared from polycrystalline silicon by the Czochralski method. Memory chips with a very high degree of integration as well as highly efficient computer chips have recently been realized.
In a short periodic table, silicon is a group IV element and has four valence-electrons. Although silicon semiconductors currently represent 90% or more of all semiconductors, isoelectronic 1:1 compounds of II-VI or III-V groups form compound semiconductors and are also used for optical or ultra high-speed electronic devices. For example, ZnS, CdS, GaAs, InP, etc. are typical compound semiconductors and the development of technologies to grow single crystals of these materials is remarkable. Light emitting diodes (LED) or semiconductor lasers are important applications of compound semiconductors.
As thin films of compound semiconductors are made by MBE (molecular beam epitaxy) or MOCVD (metallorganic chemical vapor deposition), special organometallic compounds, such as trimethyl gallium Ga(CH3)3 and trimethylarsenic As(CH3)3, whichpreviously found little application, are now used industrially.
What compounds other than the examples given are suitable as semiconductors?
- Answer
-
ZnO, CdS, PbS, GaP, and InSb
Superconductivity is a phenomenon of zero electrical resistance below a critical temperature, Tc, and was discovered in 1911 by Kamerlingh Onnes (1913 Nobel Prize for physics), who succeeded in liquefying helium during his experiments to measure the electrical resistance of mercury at ultra low temperatures. About 1/4 of the elements, such as Nb (Tc = 9.25 K), In, Sn, and Pb behave as superconductors and more than 1000 alloys and intermetallic compounds are also superconductors, but only Nb-Ti alloy (Tc = 9.5 K) and Nb3Sn (Tc = 18 K) find application. Nb3Sn, Nb3Ge, V3Ga, etc., are cubic A-15 type compounds, in which transition metal atoms are aligned in chains, and interatomic distances are shorter than those in the crystalline bulk metal, raising the density of states of the conduction band and the critical temperature, Tc, of the compound.
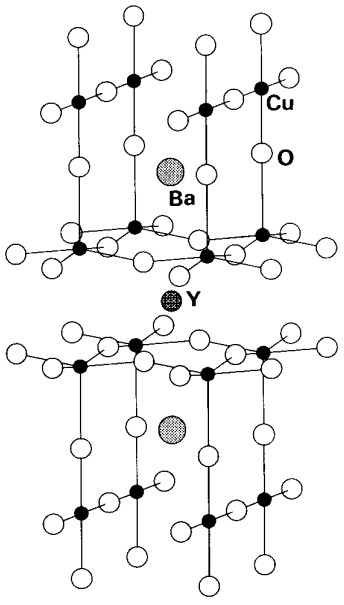
Among inorganic compound superconductors, chalcogenide compounds MxMo6X8 (X = S, Se, Te, and M = Pb, Sn, etc.) of molybdenum called Chevrel phases and high-temperature superconductors of copper oxide derivatives, which J. G. Bednortz and K. A. Müller discovered in 1986 (1987 Nobel Prize for physics), have attracted attention. Chevrel phases have structures (refer to Section 4.4) in which hexanuclear cluster units of molybdenum are joined and the highest Tc is only 15 K of PbMo6S8, but the superconductive state is not broken even in strong magnetic fields. In the copper oxide system, more than 100 similar compounds have been prepared since the first discovery and the highest Tc so far discovered is 134 K. A typical compound, YBa2Cu3O7-x, has a structure (Figure \(\PageIndex{4}\)) in which CuO5 square pyramids and CuO4 planes are connected by corner-sharing, Ba and Y are inserted between them, and the oxygen content is non-stoichiometric.

On the other hand, molecular superconductors have also been studied. Representative donor-acceptor complexes are composed of TTF and BEDT-TTF (Figure \(\PageIndex{5}\)) as electron donors, and ClO4- or [Ni(dmit)2]2- as electron acceptors. The first example of this kind of superconductor was discovered in 1980, and of the about 50 complexes known at present, the highest Tc is 13K. Recently (1991) fullerene C60 doped with alkali metals showed a Tc of about 30K.
Although thousands of superconductors are known, only a few of them find ap pound superconductors are very brittle; either it is difficult to ake plication. Because com m them into wires or only small single crystals are obtained. It will take considerable time before some of them find practical use. Therefore, mainly Nb-Ti wires are used as the superconducting magnets of analytical NMR, medical MRI (magnetic resonance imaging instrument) or maglev trains, etc. Efforts are concentrated on discovering materials that have suitable mechanical and other properties by cooperation between inorganic chemistry and solid-state physics.
Various metal oxides are used as thermistors (temperature sensitive resistance device), varistors (nonlinear resistance device), capacitors, etc. For example, BaTiO3, with a perovskite structure, and SrTiO3, etc. can be used for any of the above-mentioned purposes. Ionic conduction materials are also called solid electrolytes and \(\alpha\)-AgI, \(\beta\)-Al2O3, stabilized zirconia (a part of Zr in ZrO2 is replaced by Ca or Y), etc. are used in solid state batteries or fuel cells.
(b) Magnetism
Magnetic materials are divided into hard (permanent magnets) and soft magnetic materials. Permanent magnets are indispensable to machines using motors and MRI, which requires a high magnetic field. Japan has a strong tradition in the development of magnets, and has made many epoch-making magnetic materials for practical use. Alnico magnets with Fe, Ni, and Al as their main constituents, ferrite magnets composed of solid solutions of CoFe2O4 and Fe3O4, cobalt-rare earth magnets such as SmCo5, and Nb-Fe-B magnets were especially significant achievements. Since soft magnetic materials are strongly magnetized in weak magnetic fields, they are most suitable for use as core materials in transformers. Hard magnetic properties are necessary for the stable maintenance of information whereas soft magnetic properties are required for recording and over-writing information in magnetic recording materials such as magnetic tapes, floppy disks, and hard disks. Although \(\gamma\)-Fe2O3 is a typical magnetic powder used for these purposes, Co+ or crystalline CrO2 is added to it to improve its magnetic properties. Recording materials as well as semiconductor devices are indispensable to our modern information-oriented society, and the role played by inorganic chemistry in the improvement of the performance of these materials is significant. Recently, ferromagnetism of organic compounds or metal complexes has been discovered, in which unpaired spins are aligned parallel in a molecule and coupled ferromagnetically. The study of molecular magnets has the subject of intensive investigation. Molecular design to couple paramagnetic metal complexes and to make spins parallel is an interesting subject in coordination chemistry.
(c) Optical properties
Mainly inorganic substances are used as materials for optical applications. The optical fiber in particular has been used for optical communications on a large scale, and has had a major social influence in information communication. A necessary property of good optical glass materials is the transmission of information to distant places with little optical loss. Silica fibers are manufactured by lengthening silica glass rods produced from silica grains. The silica is made from ultra pure SiCl4, which is oxidized in the vapor phase by an oxyhydrogen flame. As the optical loss along fibers obtained by this method has already reached its theoretical limit, fluoride glasses are being used in the search for materials with lower levels of loss.
Compound semiconductors such as GaP are widely used as laser light emitting diodes for optical communications, CD players, laser printers, etc. A high output YAG laser is made from neodymium-doped yttrium aluminum garnet, Y3Al5O12, which is a ouble oxide of Y2O3 and Al2O3. Single crystals, such as lithium niobate, LiNbO3, are used for changing wavelength of light by means of SHG (second harmonic generation) of nonlinear optics phenomena.
8.1
Write a catalytic reaction cycle of the hydroformylation reaction which uses [RhH(CO)(PPh3)3] as a catalyst.
8.2
Describe differences between ammonia synthesis by the Harber-Bosch process and biological nitrogen fixation reactions.
8.3
A-15 type intermetallic compounds such as Nb3Sn are cubic crystals with the A3B composition. Consider how to locate each atom in such a unit cell.
Structure-function correlation
Since all the naturally occurring elements have been discovered, various bonding modes are established and the structures of compounds can be readily determined, studies of the chemical properties of inorganic compounds will give way to studies of reactions and physical properties. The synthesis of new compounds and the elucidation of structure-function correlations will be the foundations of these studies, although the is distant.
It is considerably difficult quantitatively to explain the thermal stability of a known inorganic compound using our present knowledge of theoretical chemistry and it is almost impossible fully to design compounds by a rational method. Although the selectivity of a catalytic reaction can be explained to some extent, the theoretical calculation of a reaction rate remains difficult. The relation between superconductivity and structure is not understood well, and critical temperatures cannot be predicted. Many of the structures and functions of the metalloenzymes that are the basis of biological activities are unknown. The research problems confronting the next generation of inorganic chemists are extensive, and novel solutions can be anticipated.


