13.5.2: Cyclic π systems

Arene or aromatic ligands are the subject of this post, the second in our series on π-system ligands. Arenes are dative, L-type ligands that may serve either as actors or spectators. Arenes commonly bind to metals through more than two atoms, although η2-arene ligands are known. Structurally, most η6-arenes tend to remain planar after binding to metals. Both “normal” bonding and backbonding are possible for arene ligands; however, arenes are stronger electron donors than CO and backbonding is less important for these ligands. The reactivity of arenes changes dramatically upon metal binding, along lines that we would expect for strongly electron-donating ligands. After coordinating to a transition metal, the arene usually becomes a better electrophile (particularly when the metal is electron poor). Thus, metal coordination can enable otherwise difficult nucleophilic aromatic substitution reactions.

General Properties

The coordination of an aromatic compound to a metal center through its aromatic π MOs removes electron density from the ring. I’m going to forego an in-depth orbital analysis in this post, because it’s honestly not very useful (and overly complex) for arene ligands. π → dσ (normal bonding) and dπ → π* (backbonding) orbital interactions are possible for arene ligands, with the former being much more important, typically. To simplify drawings, you often see chemists draw “toilet-bowl” arenes involving a circle and single central line to represent the π → dσ orbital interaction. Despite the single line, it is often useful to think about arenes as L3-type ligands. For instance, we think of η6-arenes as six-electron donors.

Multiple coordination modes are possible for arene ligands. When all six atoms of a benzene ring are bound to the metal (η6-mode), the ring is flat and C–C bond lengths are slightly longer than those in the free arene. The ring is bent and non-aromatic in η4-mode, so that the four atoms bound to the metal are coplanar while the other π bond is out of the plane. η4-Arene ligands show up in both stable complexes (see the figure below) and reactive intermediates that possess an open coordination site. To generate the latter, the corresponding η6-arene ligand undergoes ring slippage—one of the π bonds “slips” off of the metal to create an open coordination site. We’ll see ring slippage again in discussions of the aromatic cyclopentadienyl and indenyl ligands.

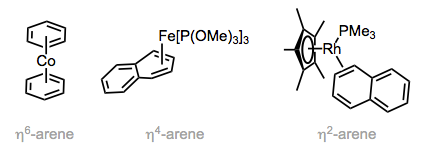
Arene ligands exhibit multiple coordination modes.

Even η2-arene ligands bound through one double bond are known. Coordination of one π bond results in dearomatization and makes η2-benzene behave more like butadiene, and furan act more like a vinyl ether. With naphthalene as ligand, there are multiple η2 isomers that could form; the isomer observed is the one that retains aromaticity in the free portion of the ligand. In fact, this result is general for polycyclic aromatic hydrocarbons: binding maximizes aromaticity in the free portion of the ligand. In the linked reference, the authors even observed the coordination of two different rhodium centers to naphthalene—a bridging arene ligand! Other bridging modes include σ, π-binding (the arene is an LX-type ligand, and one C–M bond is covalent, not dative) and L2-type bridging through two distinct π systems (as in biphenyl).

Arene ligands are usually hydrocarbons, not heterocycles. Why? Aromatic heterocycles, such as pyridine, more commonly bind using their basic lone pairs. That said, a few heterocycles form important π complexes. Thiophene is perhaps the most heavily studied, as the desulfurization of thiophene from fossil fuels is an industrially useful process.

Dr. Michael Evans (Georgia Tech)

Bonding in Ferrocene

Ferrocene was the first metallocene to be discovered and characterized. The structure of ferrocene is shown below.

Figure \(\PageIndex{9}\): The sandwich structure of ferrocene

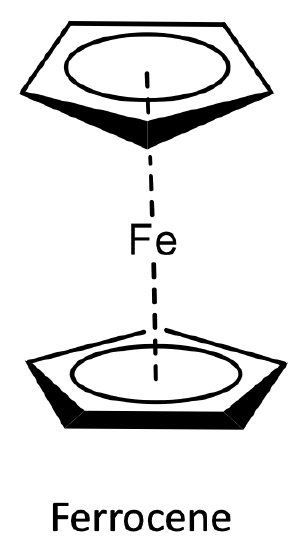
Can the stability of the ferrocene structure also be explained by molecular orbital theory? Let us check! First, we need to decide on the point group. We will make the simplification that the two C_p cyclopentadienyl rings are in eclipsed formation, and then the point group is D_5h. Actually, the rings are in staggered confirmation and the point group is D_5d, but the energy difference is minimal, and there is a very small activation barrier between the two conformers.

\begin{array}{|c|rrrrrrrr|cc|}
\hline \bf{D_{5h}} & E & 2C_5 & 2C_5^2 & 5C_2 & \sigma _h & 2S_5 & 2S_5^2 & 5 \sigma_h & h=20 & \\
\hline A_{1}’ & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & & x^2+y^2, \; z^2\\A_{2}’ & 1 & 1 & 1 & -1 & 1 & 1 & 1 & -1 & R_z & \\
E_{1}’ & 2 & 2cos(72 ^{\circ}) & 2cos(144 ^{\circ}) & 0 & 2 & 2cos(72 ^{\circ}) & 2cos(144 ^{\circ}) & 0 & (x, \; y) & \\
E_{2}’ & 2 & 2cos(144 ^{\circ}) & 2cos(72 ^{\circ}) & 0 & 2 & 2cos(144 ^{\circ}) & 2cos(72 ^{\circ}) & 0 & & (x^2-y^2,\; xy) \\
A_{1}” & 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 & & \\
A_{2}” & 1 & 1 & 1 & -1 & -1 & -1 & -1 & 1 & z & \\
E_{1}” & 2 & 2cos(72 ^{\circ}) & 2cos(144 ^{\circ}) & 0 & -2 & -2cos(72 ^{\circ}) & -2cos(144 ^{\circ}) & 0 & (R_x,\;R_y) & (xz,\; yz) \\
E_{2}” & 2 & 2cos(144 ^{\circ}) & 2cos(72 ^{\circ}) & 0 & -2 & -2cos(144 ^{\circ}) & -2cos(72 ^{\circ}) & 0 & & \\
\hline \end{array}

We can define the z-axis standing perpendicular to the Cp rings, and the xy plane to be coplanar with the Cp rings.

Figure \(\PageIndex{18}\): The coordinate system for ferrocene, Fe valence orbitals, and their symmetry types.

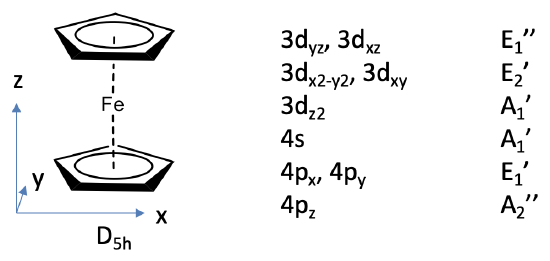
The Fe 3d, 4s and 4p orbitals will be our frontier orbitals and we can read their symmetry types from the character table of D_5h. The 3d_xz and 3d_yz have E₁’’ symmetry, the 3d_x²-y² and the 3d_xy have E₂’ symmetry, the 3d_z² has A₁’ symmetry, the 4s has A₁’ symmetry, and the 4p_x and the 4p_y orbitals have E₁’ symmetry, and the 4p_z has A₂’’ symmetry.

Next, we need to determine the ligand group orbitals. We know that the π-ligand molecular orbitals are the ones that donate the electrons into the metal-orbitals, thus we have to have a closer look at these orbitals. The π-MOs of the ligand are made from the five 2p_z orbitals of the carbon atoms that stand perpendicular to the ring. This means that there are 5 MOs to consider.

Figure \(\PageIndex{19}\): MOs of the cyclopentadienyl ligand and their relative energy

You can see the five MOs and their relative energy above. One is strongly bonding and has no node. Then, there are two double-generate weakly bonding ones that have one node, and finally there are two anti-bonding ones that have two nodes. Because the cyclopentadienyl anion has six π electrons, the bonding MO and the two weakly bonding MOs are full, the anti-bonding MOs are empty.

Because we have two Cp^- anions to consider we have overall 10 MOs to combine. We would therefore expect ten ligand group orbitals (LGOs). We can determine their symmetry type by determining the reducible and irreducible representations. The results are shown below.

Figure \(\PageIndex{20}\): 0-node LGOs

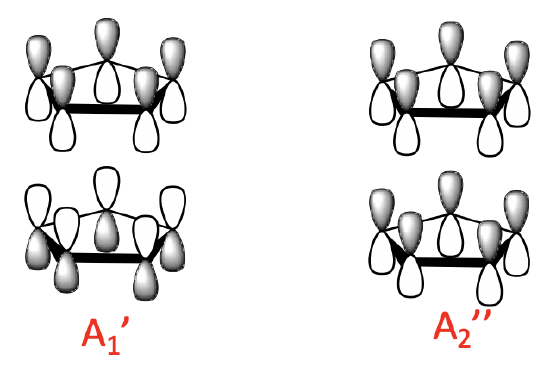
We can generally divide the LGOs into three groups with a different number of nodes. There are two 0-node LGOs with A₁’ and A₂’’ symmetry. They are made from the 0-node MOs of the ligand. There is a bonding an anti-bonding combination possible. In the bonding combination the 0–node ligand MOs have the lobes with the same algebraic sign pointing toward each other. The anti-bonding combination has the lobes with opposite algebraic sign pointing toward each other.

Figure \(\PageIndex{21}\): 1-node LGOs

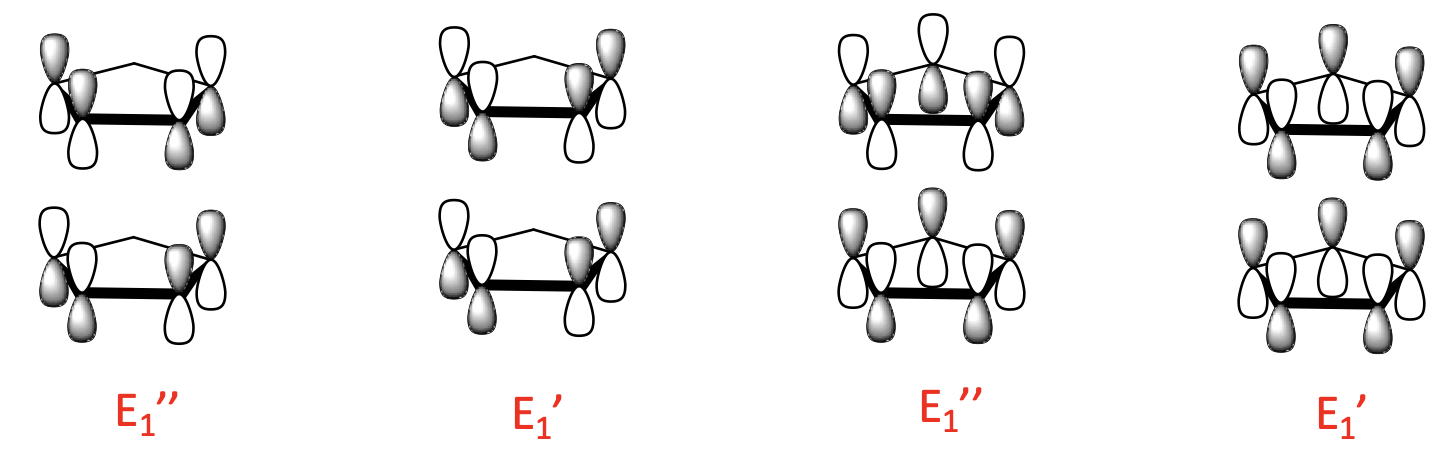
There are four 1-node LGOs with E₁’ and E₁’’ symmetry. They are constructed from the two 1-node ligand MOs. Like for the 0-node orbitals, there is a bonding and an anti-bonding combination possible.

Figure \(\PageIndex{22}\): 2-node LGOs

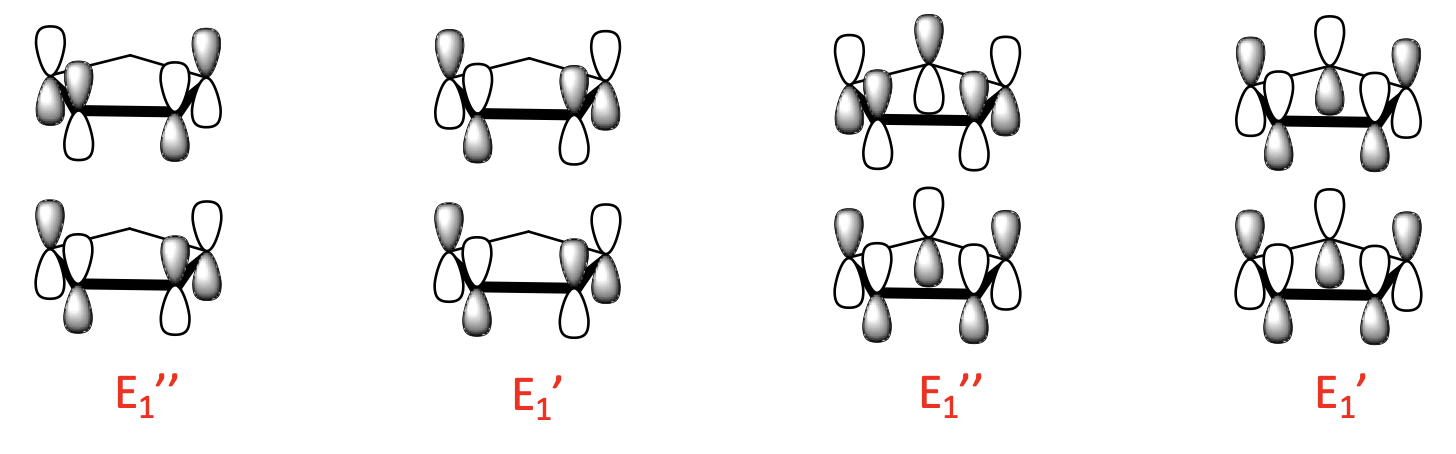
Finally, there are four 2-node LGOs with E₂’ and E₂’’ symmetry. They are made from the 2-node ligand MOs and there is also a bonding and an anti-bonding combination possible.

The Molecular Orbital Diagram of Ferrocene

Figure \(\PageIndex{23}\): MO diagram of ferrocene

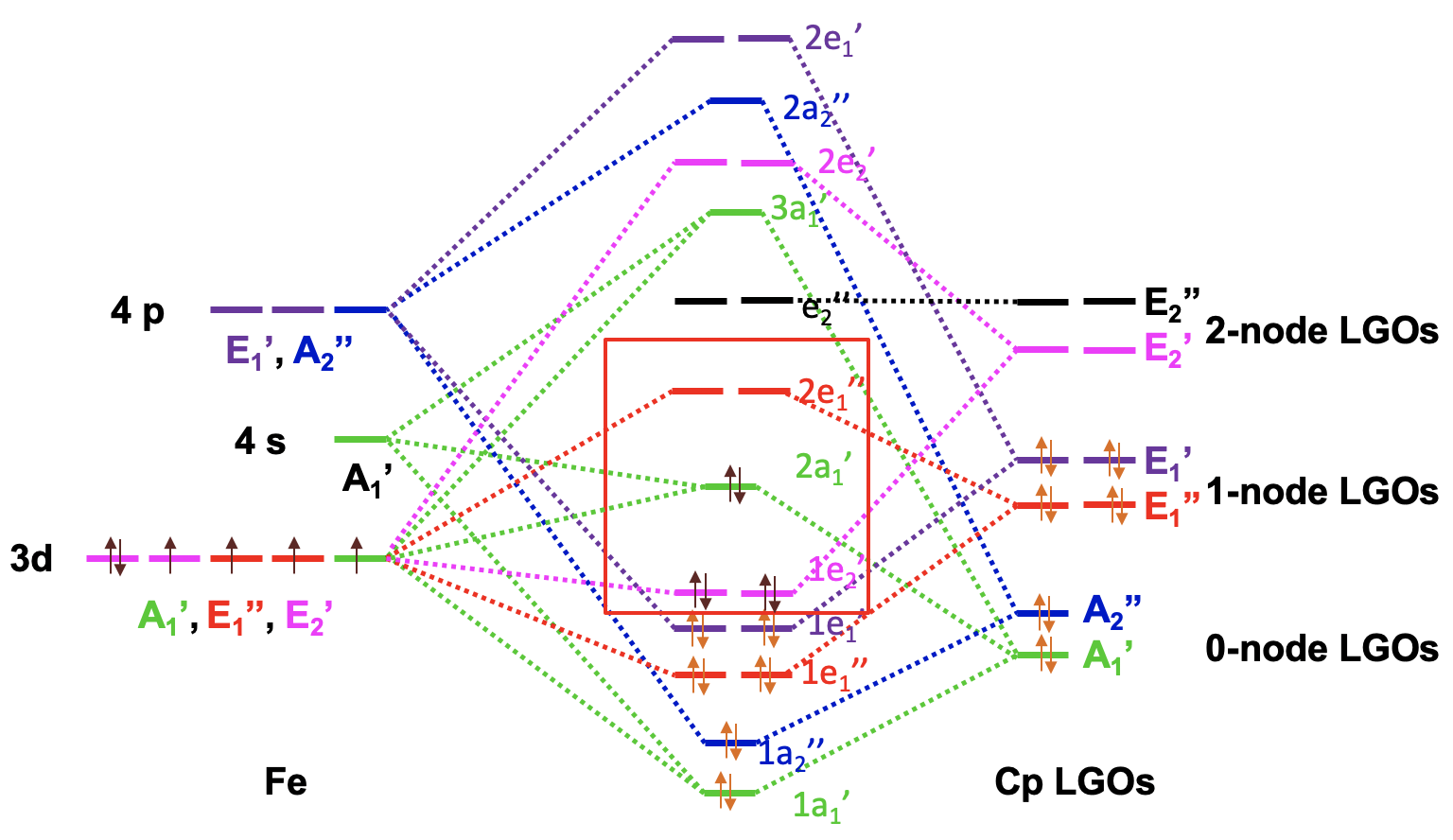
Now we have all the information to draw the molecular orbital diagram of ferrocene. As usual we plot the metal frontier orbitals on the left and label their symmetry. We plot the Cp LGOs on the right and also label the symmetry. We can order the LGOs according to energy with the 0-node LGOs having the lowest energy and the 2-node LGOs having the highest energy. Then, we can start to combine orbitals of the same symmetry type to form MOs. There are two metal AOs of the A₁’ type and one A₁’ LGO giving three MOs of this symmetry type, one bonding, one approximately non-bonding, and third one anti-bonding. We can connect AOs, LGOs, and MOs with dotted lines. Next, we can combine the A₂’’ AO and the A₂’’ LGO to form a bonding and an anti-bonding MO. We again connect the AOs, LGOs, and MOs with dotted lines. Then, we can produce two bonding e₁’’ and two anti-bonding e₁’’ MOs from the E₁’’ metal AOs and the E₁’’ LGOs and connect the orbitals with dotted lines. There are two E₁’ LGOs and two E₁’ AOs that can be combined to two bonding 1e₁’ and two anti-bonding 2e₁’ MOs and we again connect the orbitals with dotted lines. The two E₂’ LGOs can be combined with the two E₂’ d-orbitals to form a pair of bonding 1e₂’ and anti-bonding 2e₂’ molecular orbitals. Lastly, we notice that the E₂’’ LGOs do not find a partner, and we have to write them as non-bonding with the same energy into the MO diagram.

Now we need to fill the electrons into the orbitals. The ligands have twelve electrons overall. They can be filled into the six orbitals of the lowest energy. This fills the 1a₁’, the 1a₂’’, the 1e₁’’, the and 1e₁’ orbitals. We notice that all MOs are bonding which supports the stability of the molecule. We still need to consider the metal d-orbitals. We have an Fe²⁺ ion and thus six metal d-electrons. They would go into the 1e₂’ orbital which is bonding and the 2a₁’ orbital which is weakly bonding. The 2a₁ is the HOMO, and the next higher 2e₁’’ is the LUMO. We can see that we can fill all metal electrons into bonding MOs. The LUMO is an anti-bonding orbital, and thus overall all bonding MOs are filled, and no non-bonding and anti-bonding orbitals need to be filled. This is the ideal situation for a stable molecule. We can also see that the MO diagram explains the 18 electron rule. All 18 electrons are in bonding MOs.

We can consider the 1e₂’, the 2a₁’, and the 2e₁’’ metal d-orbitals in the ligand field produced by the Cp-ligands as these 5 orbitals can hold the maximum possible number of 10 d-electrons, have similar energy then the d-orbitals, and have contributions from them.

Metallocenes with other cyclic π-ligands

Is it possible to make metallocenes with other π-conjugated rings but the cylopentadienyl anion?

Figure \(\PageIndex{24}\): Bis-(benzene) chromium

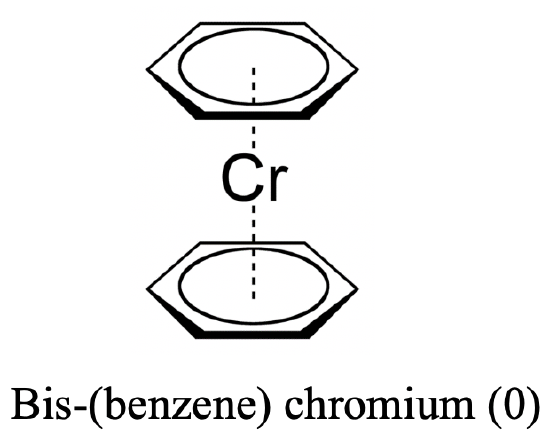
The answer is yes, for instance benzene is known to act as a ligand bis-(benzene) chromium (0). In this case the ligand acts as a ƞ⁶-ligand because all six carbon atoms are involved in the bonding. Why does chromium give stable metallocene complex with benzene? We can explain this again with the 18 electron rule. In bis-(benzene) chromium (0), chromium is in the oxidation state 0 because the benzene ligand has no charge. Thus, chromium contributes six electrons. Adding the 12 π-electrons from the two benzene ligands gives 18 electrons.

Other cyclic π-ligands

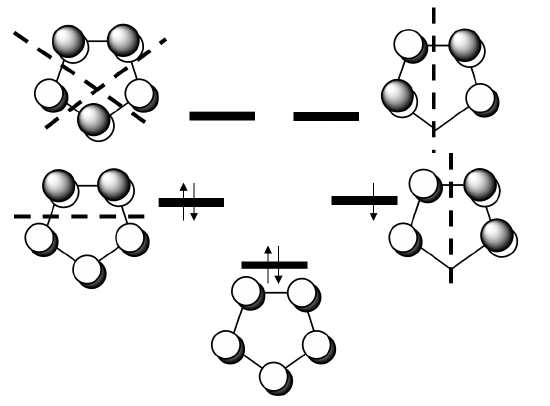
Also cyclobutadiene can act as a cylic π-ligand in complexes. The cyclobutadiene is is different from the cyclopentadienyl anion and the benzene ligand in two ways. Firstly, it has much more ring strain then the previous two, and secondly it is not an aromatic, but an anti-aromatic ligand. Remember, we have an aromatic ring when there are 4n+2 π-electrons, whereby n is an inter number. This means that rings with two (n=0), six (n=1), and ten (n=2) π-electrons are aromatic. Anti-aromatic rings are those that have 4n electrons, such as four (n=1), eight (n=2) and so forth. Cyclobutadiene has four electrons, and thus it is anti-aromatic. Anti-aromatic rings are less stable than aromatic ones because not all π-electrons are in bonding molecular orbitals. Let us illustrate this by constructing the MO diagram for the π-system of the cyclobutadiene molecule (Figure \(\PageIndex{25}\))

Figure \(\PageIndex{25}\): MO diagram for the π-system of the cyclobutadiene molecule

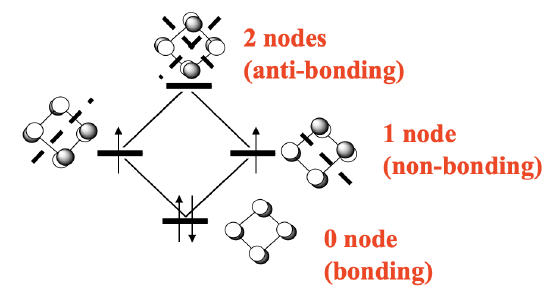
The π-system is made of four carbon atoms contributing a half-filled 2p_z orbital each (if we define the plane of the molecule as the xy plane). That makes four p-orbitals with four electrons that give four molecular orbitals. There is a bonding MO with no node, two doubly-degenerate non-bonding ones with one node, and one anti-bonding one with two nodes (Figure \(\PageIndex{25}\)). There are four electrons. We can fill two electrons into the bonding MO, but the other two must go into the two non-bonding ones under obedience of Hund’s rule.

Jahn-Teller distortion in cyclobutadiene

One may think that the cyclobutadiene is a square planar molecule because of complete delocalization of the π-electrons, but that is actually not the case. There are two shorter double-bonds and two longer single-bonds, and the shape of the molecules is a rectangle. This means that the two double bond are localized. We can view this effect as a Jahn-Teller distortion.

Figure \(\PageIndex{26}\): Jahn-Teller distortion in cyclobutadiene

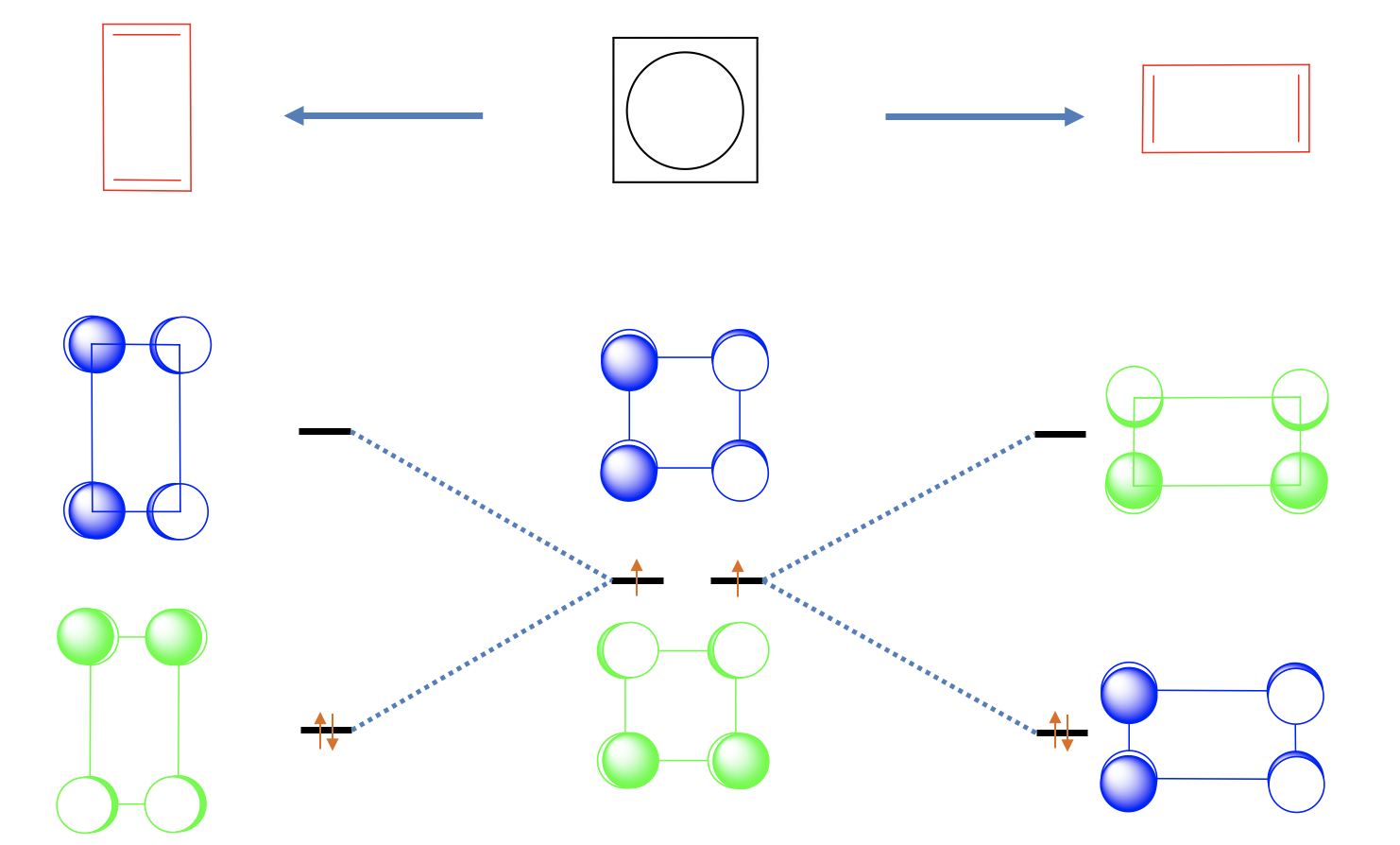
The distortion of the square to form a rectangle is energetically favorable because it lowers the energy of the two non-bonding electrons. Why? Let us look at the non-bonding orbital 1 first and elongate in x-direction, and squeeze in y-direction (Figure \(\PageIndex{26}\)). We can see that we bring the p-orbitals with bonding interactions further apart, and bring those with anti-bonding interactions closer together. This means that the energy of this orbital goes up and the orbital becomes anti-bonding. Let us do the same with non-bonding orbital 2. We see that the opposite happens. The bonding interactions are enhanced and the anti-bonding interactions are weakened. Therefore, this orbital becomes bonding and the energy goes down. We can now fill the two electrons into the bonding MO. We see that we have lowered the energy of the electrons through the distortion.

We could also have squeezed in x-direction and elongated in y-direction. In this case orbital 1 would have become bonding and orbital 2 anti-bonding. However, this distortion is symmetry-equivalent to the previous one, and does not produce a new molecule. Both molecules can be superposed by a simple 90° rotation.

Cyclobutadiene as ƞ⁴-ligand

Cyclobutadiene (Cb) in its free form is not stable because of the high ring strain and the anti-aromaticity, but complexes with cyclobutadiene as a ligand are stable. We would expect that 18 electron complexes are most stable.

Figure \(\PageIndex{27}\): Complexes with cyclobutadiene

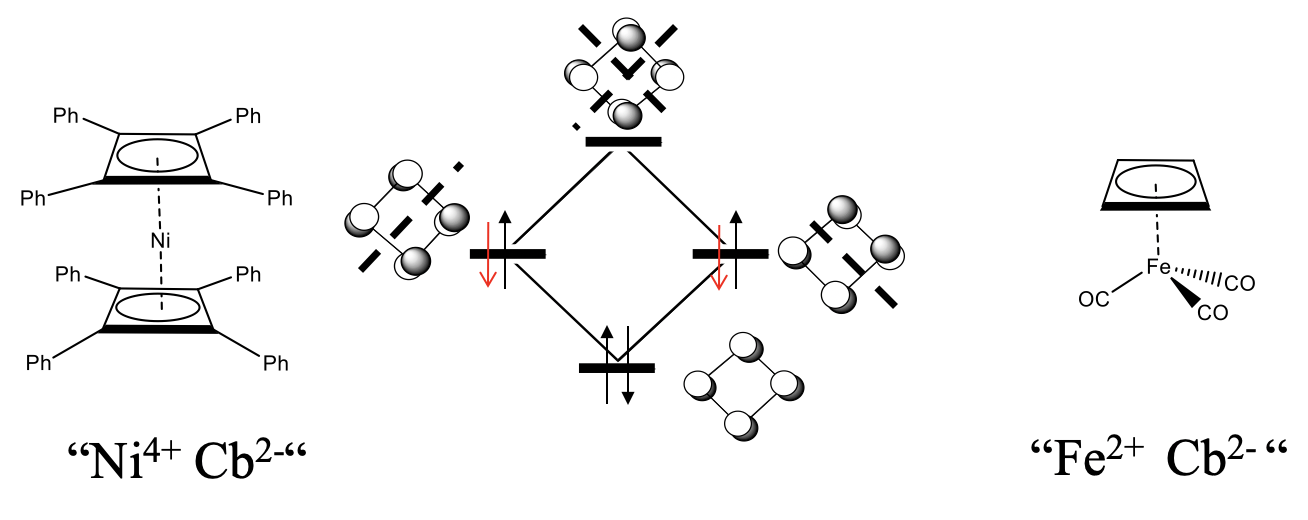
What would be an 18 electron sandwich complex with two cyclobutadiene ligands? Because each cyclobutadiene contributes four electrons, ten electrons would need to come from the metal, and we would expect a nickel cyclobutadienyl complex Ni(Cb)₂. This complex is not known, but derivatives are. For example a Ni complex with two tetraphenyl butadiene ligands are known (Figure \(\PageIndex{27}\)). Another example is the butadienyl tricarbonyl iron (0) complex. Interestingly, when cyclobutadiene acts as a ƞ⁴-ligand, then it is not distorted, but square planar. An explanation is that we can formally treat the cyclobutadiene ligand as an Cb^2- ligand binding to a metal cation. For instance in FeCb(CO)₃ the Fe would be an Fe²⁺, in the nickel complex, the nickel would be a Ni⁴⁺. The Cb^2- anion would formally aromatic because it has 4n+2=6 electrons. The additional two electrons would be in the non-bonding orbitals. Because the two non-bonding orbitals are completely filled now, there would be no longer a driving force for the distortion. Note though that is is a formal view only, and there are arguments that speak against this view. One is that the addition of the two electrons to the ligand should further destabilize the ring because the added electrons are non-bonding. Aromaticity would rather be achieved by removing two electrons to form a Cb²⁺ cation that would have only two electrons in the bonding orbital.

Cyclooctetraene (cot) as a ligand

Also metallocenes with cyclooctatetraene (cot) acting as ƞ⁸-ligand is known. However, because of the large ring size only metals with large atomic radii, can make metallocenes with this ligand. For example uranium makes a uranocenes with two cyclooctatetraene ligands (Figure \(\PageIndex{28}\)).

Figure \(\PageIndex{28}\): Aromatic Cot^2- ligand

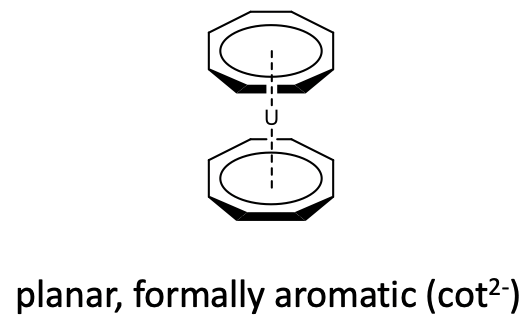
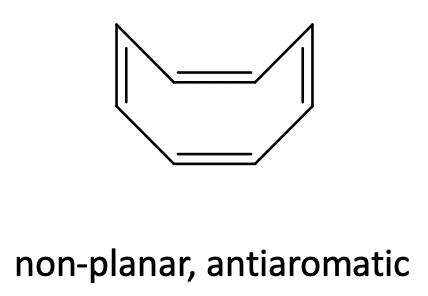
Like cyclobutadiene, cyclooctatetraene is an anti-aromatic ligand with 4n=8 π-electrons (n=2). In the free cyclooctatetraene molecule is non-planar and the π-electrons are localized (Figure \(\PageIndex{29}\)).

Figure \(\PageIndex{29}\): Free cyclooctatraene is non-planar, thus \(\pi\) electrons are localized.

In metallocenes however, the ring becomes planar (Figure \(\PageIndex{28}\)). One can again formally explain that by assuming an aromatic cot^2- ligand that binds to a metal 2+ cation, however one should keep in mind again that this is a formal view and not necessarily reflects the bonding situation in the compound.

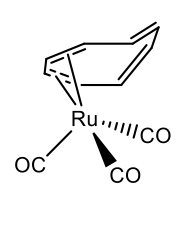
Metals having smaller atomic radius can bind to cot in ƞ², ƞ⁴, and less commonly in ƞ⁶-mode. The 18 electron rule holds in most cases. For instance, cot can make a ƞ⁴-complex in tricarbonyl cyclooctatetraene ruthenium (0) (Figure \(\PageIndex{30}\)).

Figure \(\PageIndex{30}\): tricarbonyl cyclooctatetraene ruthenium (0)

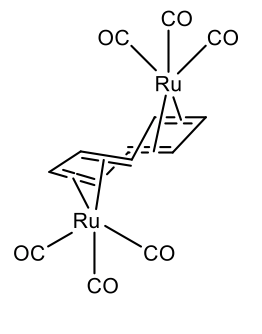
Also two metals can bind to a single cot-ligand. This is for instance realize in μ-cyclooctetraene bis(tricarbonyl ruthenium (0) (Figure \(\PageIndex{31}\)).

Figure \(\PageIndex{31}\): bis(tricarbonyl) cyclooctetraene ruthenium (0)

---

Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.