13.5.1: Linear π Systems
- Page ID
- 385586
General Properties
The π bonding orbitals of alkenes, alkynes, carbonyls, and other unsaturated compounds may overlap with dσ orbitals on metal centers. This is the classic ligand HOMO → metal LUMO interaction that we’ve beaten into the ground over the last few posts. Because of this electron donation from the π system to the metal center, coordinated π systems often act electrophilic, even if the starting alkene was nucleophilic (the Wacker oxidation is a classic example; water attacks a palladium-coordinated alkene). The π → dσ orbital interaction is central to the structure and reactivity of π-system complexes.
Then again, a theme of the last three posts has been the importance of orbital interactions with the opposite sense: metal HOMO → ligand LUMO. Like CO, phosphines, and NHCs, π systems are often subject to important backbonding interactions. We’ll focus on alkenes here, but these same ideas apply to carbonyls, alkynes, and other unsaturated ligands bound through their π clouds. For alkene ligands, the relative importance of “normal” bonding and backbonding is nicely captured by the relative importance of the two resonance structures in the figure below.
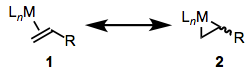
Resonance forms of alkene ligands.
Complexes of weakly backbonding metals, such as the electronegative late metals, are best represented by the traditional dative resonance structure 1. But complexes of strong backbonders, such as electropositive Ti(II), are often best drawn in the metallacyclopropane form 2. Organic hardliners may have a tough time believing that 1 and 2 are truly resonance forms, but several studies—e.g. of the Kulinkovich cyclopropanation—have shown that independent synthetic routes to metallacyclopropanes and alkene complexes containing the same atoms result in the same compound. Furthermore, bond lengths and angles in the alkene change substantially upon coordination to a strongly backbonding metal. We see an elongation of the C=C bond (consistent with decreased bond order) and some pyramidalization of the alkene carbons (consistent with a change in hybridization from sp2 to sp3). A complete orbital picture of “normal” bonding and backbonding in alkenes is shown in the figure below.
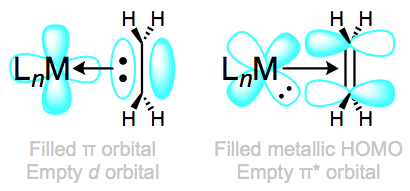
Normal bonding and backbonding in alkene complexes.
Here’s an interesting question with stereochemical implications: what is the orientation of the alkene relative to the other ligands? From what we’ve discussed so far, we can surmise that one face of the alkene must point toward the metal center. Put differently, the bonding axis must be normal to the plane of the alkene. However, this restriction says nothing about rotation about the bonding axis, which spins the alkene ligand like a pinwheel. Is a particular orientation preferred, or can we think about the alkene as a circular smudge over time? The figure below depicts two possible orientations of the alkene ligand in a trigonal planar complex. Other orientations make less sense because they would involve inefficient orbital overlap with the metal’s orthogonal d orbitals. Which one is favored?
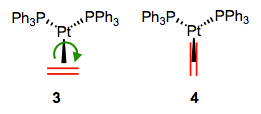
Two limiting cases for alkene orientation in a trigonal planar complex.
First of all, we need to notice that these two complexes are diastereomeric. They have different energies as a result, so one must be favored over the other. Naive steric considerations suggest that complex 4 ought to be more stable (in most complexes, steric factors dictate alkene orientation). To dig a little deeper, let’s consider any electronic factors that may influence the preferred geometry. We’ve already seen that electronic factors can overcome steric considerations when it comes to complex geometry! To begin, we need to consider the crystal field orbitals of the complex as a whole. Verify on your own that in this d10, Pt(0) complex, the crystal-field HOMOs are the dxy and dx2–y2 orbitals. Where are these orbitals located in space? In the xy-plane! Only the alkene in 3 can engage in efficient backbonding with the metal center. In cases when the metal is electron rich and/or the alkene is electron poor, complexes like 3 can sometimes be favored in spite of sterics. The thought process here is very similar to the one developed in an earlier post on geometry. However, please note that this situation is fairly rare—steric considerations often either match or dominate electronics where alkenes are concerned.