13.4.3: Hydrides and Dihydrogen Complexes
- Page ID
- 385583
Ligands can, shockingly enough, bind through the electrons in their own \(\sigma\) bonds in an L-type fashion. This binding mode depends as much on the metal center as it does on the ligand itself—to see why, we need only recognize that \(\sigma\) complexes look like intermediates in concerted oxidative additions. With a slight reorganization of electrons and geometry, an L-type \(\sigma\) ligand can become two X-type ligands. Why, then, are \(\sigma\) complexes stable? How can we control the ratio of \(\sigma\) complex to X2 complex in a given situation? How does complexation of a \(\sigma\) bond change the ligand’s properties? We’ll address these questions and more in this post.
General Properties
The first thing to realize about \(\sigma\) complexes is that they are highly sensitive to steric bulk. Any old \(\sigma\) bond won’t do; hydrogen at one end of the binding bond or the other (or both) is necessary. The best studied \(\sigma\) complexes involve dihydrogen (\(\ce{H2}\)), so let’s start there.
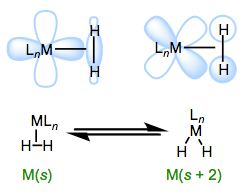
Mildly backbonding metals may bind dihydrogen “side on.” Like side-on binding in \(\pi\) complexes, there are two important orbital interactions at play here: The first is a sigma bonding interaction (\(\ce{ \sigma H-H \bond{->} d\sigma}\)), as pictured on the left in Figure \(\PageIndex{2}\); the second is a \(\pi\) bonding interaction ( \( \ce{d \pi \bond{->}} \sigma^* \ce{H–H}\)), as pictured on the right in Figure \(\PageIndex{2}\). Dihydrogen complexes can “tautomerize” to hydride \(\ce{(H)2}\) isomers through cleavage of the \(\ce{H–H}\) bond to the metal (this is an oxidative addition reaction, as discussed in the chapter on organometallic reactions).
\(\ce{H2}\) binding in an L-type fashion massively acidifies the ligand. Changes in of over thirty pKa units have been observed upon metal binding! Analogous acidifications of X–H bonds, rarely exhibit ΔpKa > 5. What’s causing the different behavior of X–H and H–H ligands? The key is to consider the conjugate base of the ligand—in particular, how much it’s stabilized by a metal center relative to the corresponding free anion. The principle here is analogous to the famous dictum of organic chemistry: consider charged species when making acid/base comparisons. Stabilization of the unhindered anion \(\ce{H^-}\) by a metal is much greater than stabilization of larger, more electronegative anions like \(\ce{HO^-}\) and \(\ce{NH2^-}\) by a metal. As a result, it’s more favorable to remove a proton from metal-complexed \(\ce{H2}\) than from larger, more electronegative X–H ligands.
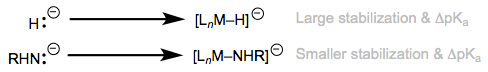
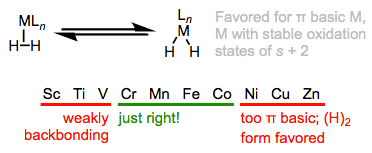
Remarkably large stabilization by an acidic metal fragment, without any counterbalancing from steric factors, explains the extreme acidification of dihydrogen upon metal binding.
The electronic nature of the metal center has two important effects on \(\sigma\) complexes. The first concerns the acidity of \(\ce{H2}\) upon metal binding. The principle here is consistent with what we’ve hammered into the ground so far. In the same way cationic organic acids are stronger than their neutral counterparts, \(\sigma\) complexes of electron-poor metals—including (and especially) cations—are stronger acids than related complexes of electron-rich metals. The second concerns the ratio of L-type to X2-type binding. We should expect more electron-rich metal centers to favor the X2 isomer, since these should donate more strongly into the \(\sigma\)*H–H orbital. This idea was masterfully demonstrated in a study by Morris, in which he showed that \(\ce{H2}\) complexes of π-basic metal centers show all the signs of X2 complexes, rather than L complexes. More generally, metal centers in \(\sigma\) complexes need a good balance of π basicity and \(\sigma\) acidity (I like to call this the “Goldilocks effect”). Because of the need for balance, \(\sigma\) complexes are most common for centrally located metals (groups 6-9).
The M–H bond in hydride complexes is a good base—anyone who’s ever quenched lithium aluminum hydride can attest to this! Intriguingly, because it’s a good base, the M–H bond can participate in hydrogen bonding with an acidic X–H bond, where X is a heteroatom. This kind of bonding, called dihydrogen bonding (since two hydrogen atoms are involved), is best described as a sort of \(\sigma\)M–H→\(\sigma\)*X–H orbital interaction. Think of it as analogous to a traditional hydrogen bond, but using a \(\sigma\) bond instead of a lone pair. Crazy, right?!
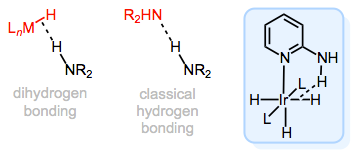
Dihydrogen bonding in metal hydrides: a sort of "interrupted protonation" of M–H.
Other kinds of \(\sigma\) complexes are known, but these are rarer than H–H complexes. One class that we’ve seen before involve agostic interactions of C–H bonds in alkyl ligands. \(\sigma\) Complexes of inorganic ligands like silanes and stannanes may involve complex bonding patterns, but we won’t concern ourselves with those here.
Hydride Complexes
Metal-hydrogen bonds, also known (misleadingly) as metal hydrides, are ubiquitous X-type ligands in organometallic chemistry. There is much more than meets the eye to most M-H bonds: although they’re simple to draw, they vary enormously in polarization and pKa. They may be acidic or hydridic or both, depending on the nature of the metal center and the reaction conditions. In this post, we’ll develop some heuristics for predicting the behavior of M-H bonds so that later, we can discuss their major modes of reactivity (acidity, radical reactions, migratory insertion, etc.).
General Properties
Metal hydrides run the gamut from nucleophilic/basic to electrophilic/acidic. Then again, the same can be said of X–H bonds in organic chemistry, which may vary from mildly nucleophilic (consider Hantzsch esters and NADH) to extremely electrophilic (consider triflic acid). As hydrogen is what it is in both cases, it’s clear that the nature of the X fragment—more specifically, the stability of the charged fragments X+ and X–—dictate the character of the X–H bond. Compare the four equilibria outlined below—the stabilities of the ions dictate the position of each equilibrium. By now we shouldn’t find it surprising that the highly π-acidic W(CO)5 fragment is good at stabilizing negative charge; for a similar reason, the ZrCp2Cl fragment can stabilize positive charge.*
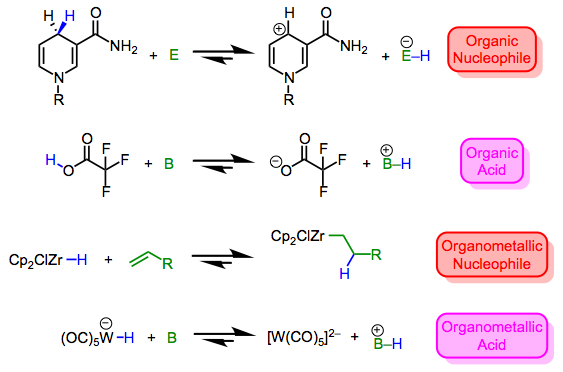
Metal-hydrogen bonds may be either hydridic (nucleophilic) or acidic (electrophilic). The nature of other ligands and the reaction conditions are keys to making predictions.
Let’s turn our attention now to homolytic M–H bond strength. A convenient thermodynamic cycle allows us to use the acidity of M–H and the oxidation potential of its conjugate base in order to determine bond strength. This clever method, employed by Tilset and inspired by the inimitable Bordwell, uses the cycle in the figure below. BDE values for some complexes are provided as well. From the examples provided, we can see that bond strength increases down a group in the periodic table. This trend, and the idea that bridging hydrides have larger BDEs than terminal M–H bonds, are just about the only observable trends in M–H BDE.
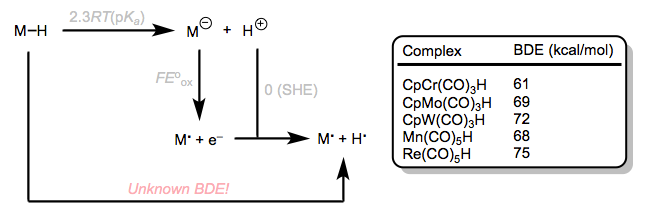
A clever cycle for determining BDEs from other known quantities, with select BDE values. I've left out solvation terms from the thermodynamic cycle. For more details, see the Tilset link above.
Why is knowing M-H BDEs useful? For one thing, the relative BDEs of M-C and M-H bonds determine the thermodynamics of β-hydride elimination, which results in the replacement of a covalent M-C bond with an M-H bond. Secondly, complexes containing weak M-H bonds are often good hydrogen transfer agents and may react with organic radicals and double bonds, channeling stannane and silane reductants from organic chemistry.
Hydricity refers to the tendency of a hydride ligand to depart as H–. A similar thermodynamic cycle relates the energetics of losing H– to the oxidation potentials of the conjugate base and the oxidized conjugate base; however, this method is complicated by the fact that hydride loss establishes an open coordination site. I’ve provided an abridged version of the cycle below. Hydricities are somewhat predictable from the electronic and steric properties of the metal center: inclusion of electron-donating ligands tends to increase hydricity, while electron-withdrawing or acidic ligands tend to decrease it. For five-coordinate hydrides that form 16-electron, square planar complexes upon loss of hydride, the bite angle of chelating phosphines plays an interesting role. As bite angle increases, hydricity does as well.
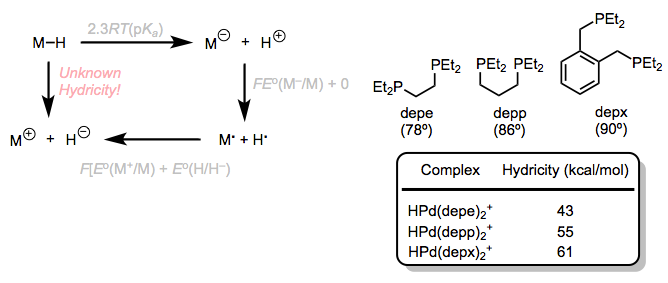
A thermodynamic cycle for hydricity, with some examples. Hydricity and bite angle are well correlated in five-coordinate palladium hydrides.
Bridging hydrides are an intriguing class of ligands. A question to ponder: how can a ligand associated with only two electrons possibly bridge two metal centers? How can two electrons hold three atoms together? Enter the magic of three-center, two-electron bonding. We can envision the M–H sigma bond as an electron donor itself! With this in mind, we can imagine that hydrides are able to bind end-on to one metal (like a standard X-type ligand) and side-on to another (like an L-type π system ligand, but using sigma electrons instead). Slick, no? We’ll see more side-on bonding of sigma electrons in a future post on sigma complexes.
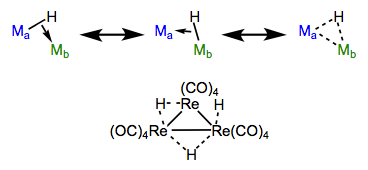
Resonance forms of bridging hydrides, with an example. Sigma complexes like these show up in other contexts, too!
Consistent with the idea that bridging is the result of “end-on + side-on” bonding, bond angles of bridging hydrides are never 180°.