11.3.7: Charge-Transfer Spectra
- Page ID
- 377934
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Charge Transfer Transitions

We are still not done with our electronic spectra. Thus far, we have only considered transitions of d-electrons between d-orbitals, and their terms. These are called d-d transitions. However, there are also so-called charge transfer transitions possible, which are not d-d transitions. We can easily see that there must be transitions other than d-d transitions when we look at the colors of d10 and d0 ions. For those, there are no d-d transitions possible. Therefore, they all should be colorless. However, that is not always true. Some of these ions are indeed colorless, but some are not (Figure \(\PageIndex{2}\)). For example, Zn2+, a d10 ion, is colorless in complexes, but not Cu(I), which is also d10. While tetrakis(acetonitrile)copper(+) is colorless, bis(phenanthrene) copper(+) is dark orange. d0 ions have similar properties: While TiF4 and TiCl4 are colorless, TiBr4 is orange, and TiI4 is brown. Some d0 species are even extremely colorful, for example, permanganate with Mn7+, which is extremely purple, and dichromate with Cr(VI), which is bright orange.
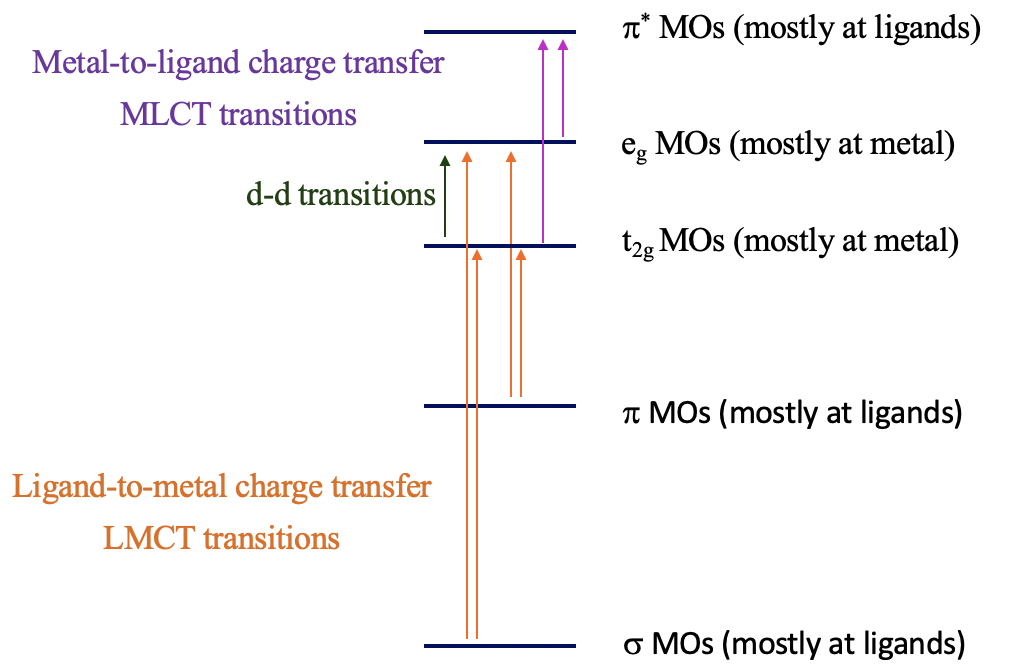
The explanation for these phenomena is charge-transfer transitions (\(\PageIndex{2}\)). There are two types of charge-transfer transitions: ligand-to-metal (LMCT) and metal-to-ligand (MLCT) charge transfer transitions. For the ligand-to-metal transitions, electrons from bonding σ and π-orbitals get excited into metal d-orbitals in the ligand field, for example the t2g and the eg orbitals in an octahedral complex. If the energy difference between the σ/π-orbitals and the d-orbitals is small enough, then this electron transition is associated with the absorption of visible light. The transition is called a ligand-to-metal transition because the ligand σ/π-orbitals are mostly located at the ligands, while the metal-d-orbitals in a ligand field are mostly located at the metal. Vice versa, the metal-to-ligand transition involves the transition of an electron from metal d-orbitals in a ligand field to ligand π*-orbitals. This essentially moves electron density from the metal to the ligand, hence the name ligand-to-metal-charge transfer transition. If the energy-difference between the ligand π* and the metal orbitals is small enough, then the absorption occurs in the visible range. Charge-transfer transitions are usually both spin- and Laporte allowed; hence, if they occur, the color is often very intense. How can we distinguish between d-d and charge transfer transitions? Charge transfer transitions often change in energy as the solvent polarity is varied (solvatochromic), as there is a change in polarity of the complex associated with the charge transfer transition. This can be used to distinguish between d-d transitions and charge-transfer bands.
LMCT Transitions
Can we predict when the energy windows between the bonding molecular orbitals and the metal d-orbitals are small enough for LMCT transitions in the visible to take place? Generally, it would be desirable if the energy of the metal orbitals were as low as possible and the energy of the bonding ligand orbitals were as high as possible. The energy of metal d-orbitals decreases with increasing positive charge at the metal because the effective nuclear charge on the metal increases. This means that very high metal oxidation states favor LMCT transitions. The d-orbitals should have few or no electrons, so that electrons can be promoted into the orbitals, and orbital energy decreases because electron-electron repulsion is minimized. Examples are Mn(VII), Cr(VI), and Ti(IV). The energy of MOs from bonding ligand orbitals increases when the ligand orbitals have high energy; this is typically the case for π-donor ligands with a negative charge (Fig. 8.2.21).


Examples of ligands are oxo- and halo ligands. This explains, for example, the LMCT transitions in permanganate. The Mn is in the very high oxidation state +7, and the ligands are oxo-ligands, which are π-donors with a 2- negative charge. The transitions are both Laporte and spin-allowed, leading to a very high intensity of light absorption, and thus color (Fig. 8.2.21).
MLCT Transitions
What are favorable metal ion and ligand properties for a metal-to-ligand transition, then? In this case we would like to keep the energy of the metal orbitals as high as possible so that the energy difference between a metal d-orbital and a π*-orbital is minimized. This is accomplished when the positive charge at the metal ion is small, and there are many d-electrons that can repel each other, thereby increasing orbital energies, for example Cu(I), Fig. 8.2.22.
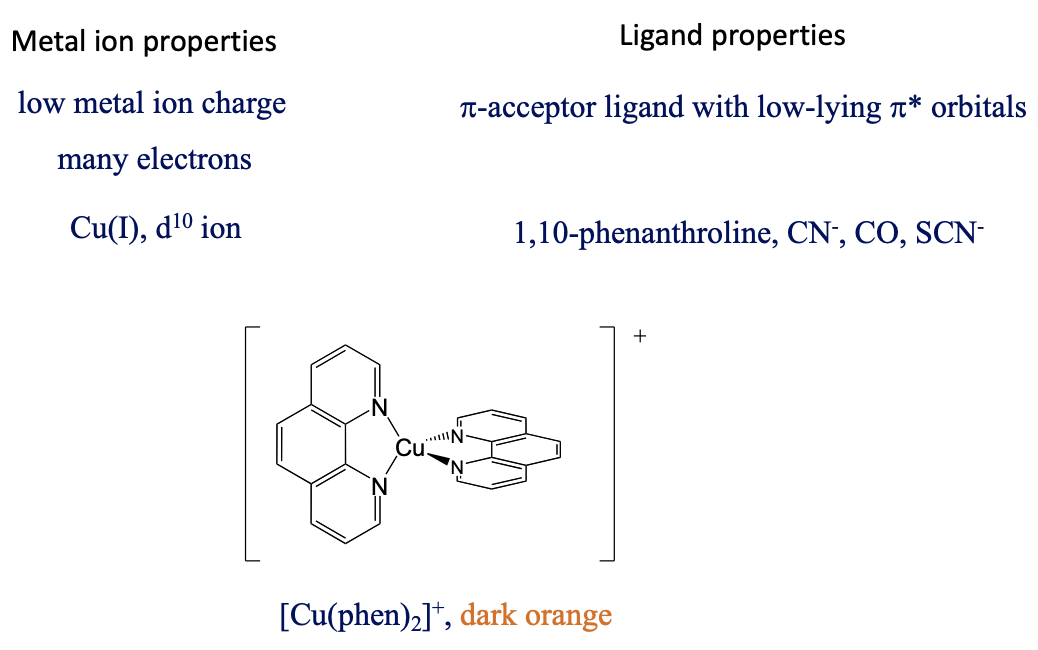
The ligand should be a π-acceptor with low-lying π*-orbitals - for example, phenanthroline, CN-, SCN-, and CO. The bis(phenanthroline) copper(+) ion, for instance, is dark orange and has an MLCT absorption band at 458 nm. This MLCT transfer is both spin and Laporte-allowed.
It should be mentioned that some complexes allow for both metal-to-ligand and ligand-to-metal transitions. For example, in the Cr(CO)6 complex, the σ-orbitals are high enough and the π*-orbitals are low enough in energy to allow for light absorption in the visible range. Finally, intraligand bands are also possible when the ligand is a chromophore.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


