11.3.6: Tetrahedral Complexes

Last updated
Save as PDF

Page ID: 377933

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Transitions in tetrahedral complexes are Laporte-allowed

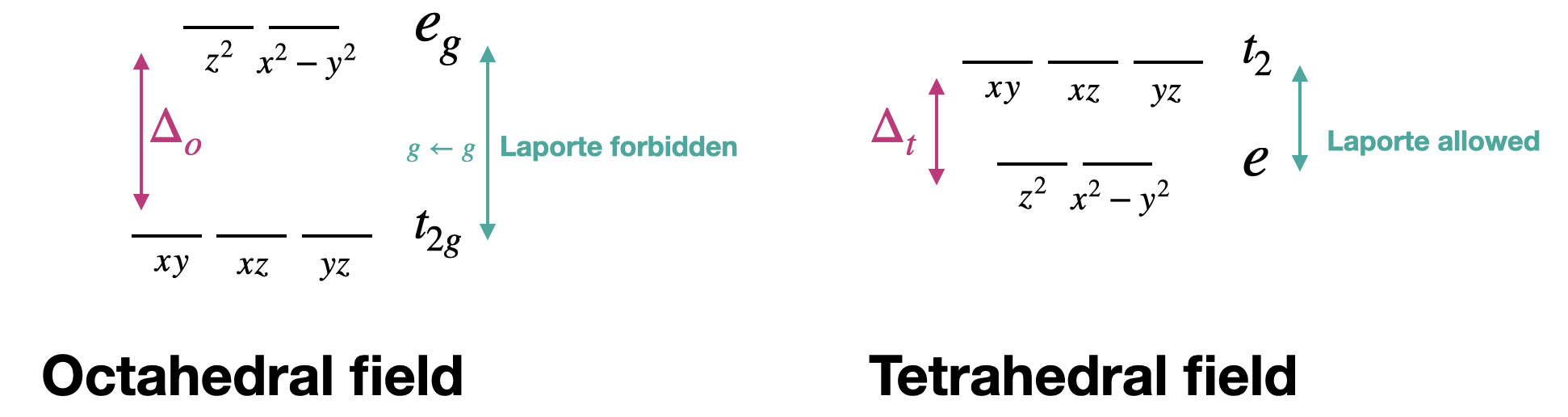
Tetrahedral metal complexes often have more intense electronic transitions than their octahedral counterparts. This is due to the fact that the \(d-d\) transitions in a tetrahedron are allowed by the Laporte selection rule, while \(d-d\) transitions in an octahedral complex are Laporte-forbidden. Recall that the Laporte selection rule applies to centrosymmetric complexes only. The Laporte rule applies to octahedral complexes but not to tetrahedral complexes because a tetrahedron does not have a center of inversion. Notice that the terms (and orbital labels) in a tetrahedron do not include the \(g\) subscripts that are present under octahedral symmetry (Figure \(\PageIndex{1}\)). The splitting pattern of a tetrahedral complex is exactly opposite to the octahedral case. In the case of a tetrahedron, however, the "\(g\)" subscripts are inappropriate because of the tetrahedron's lack of a center of inversion, and transitions between the terms in a tetrahedron do not violate the Laporte Rule.

Another way to explain this in terms of electron transitions between orbitals is through the orbital mixing required to form a tetrahedral complex. Orbital types (i.e., \(s,p,d\)) must mix to form the moleculare orbitals of a tetrahedral transition metal complex. The mixing of \(s\) and \(p\) orbitals with the \(d\) orbitals allows transitions that are forbidden in the case of pure d-orbitals.

It is also worth noting that \(\Delta_t = \frac{4}{9} \Delta_o\). The smaller \(\Delta\) for transition metals means that the tetrahedral complexes can absorb at a lower energy and longer wavelength relative to an analogous octahedron.

Figure \(\PageIndex{1}\): \(d-d\) transitions in octahedral complexes are Laporte-forbidden, while those in tetrahedral complexes are Laporte-allowed. (CC_BY_SA; Kathryn Haas)

Tanabe-Sugano diagrams for tetrahedral complexes

Due to the opposite splitting pattern, the transitions for a \(d^n\) tetrahedral complex are sufficiently represented by the \(d^{10-n}\) Tanabe-Sugano diagram (just drop the \(g\) subscripts from the diagrams). For example, the electronic spectrum of a \(d^8\) tetrahedral complex (e.g., \(\ce{[Ni(H2O)6]^2+}\)) can be interpreted using the \(d^2\) Tanabe-Sugano diagram.