9.4: Isomerism
- Page ID
- 151410
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Metal complexes present a rich, interesting, and diverse structural chemistry. Major points of variation in the structural chemistry of metal complexes include
- coordination number and coordination geometry, which involve differences in how many ligands surround a central metal and their overall geometric arrangement. Examples of the latter include the tetrahedral and square planar geometries commonly observed for four-coordinate metal centers. Tetrahedral, square planar, and octahedral coordination serve as a backdrop to the discussion of isomerism on this page. Readers who are unfamiliar with these structures might consider reading the section on coordination geometries before this one.
- structural iosmerism involves differences in how potential ligand atoms are bound to metals in a complex. Possibilities for structural isomerism include
- linkage or ambidentate isomerism
- hydrate/solvate isomerism
- ionization isomerism
- coordination isomerism.
Of these, linkage isomerism should always be considered when working with ambidentate ligands. As classifications, the last three forms of structural isomerism are mainly of academic interest since they represent permutations of ordinary structure patterns for solvates, salts, and coordination complexes, respectively.
- stereochemistry, which includes
- which coordination geometry is adopted for a metal with a given set of ligands in a particular oxidation state. For instance, [NiIICl4]2- is tetrahedral while [PtIICl4]2- is square planar. Since this geometry is usually fixed by the metal and ligands it is typically not a source of stereoisomeric varierty.
- metal-centric stereoisomerism involving possible variations in where ligands are located relative to one another around the metal. The possibilities depend on the coordination number, geometry, and number of different types of ligands. For instance, square planar complexes can exhibit cis-/trans- isomerism while tetrahedral ones cannot. Tetrahedral complexes with four different ligands exhibit R and S chirality but complexes of that type are relatively rare. The more common cases include cis and trans isomerism in square planar complexes and cis & trans-, mer & fac-, and \(\Lambda\) & \(\Delta\) isomerism in octahedral ones, although some multidentate ligands present additional possibilities for stereochemical variation
- Stereoisomerism centered on the ligands bound to a metal center. Possibilities include
- stereoisomerism inherent to a ligand. This would include cases where the ligand itself is chiral or, as in the case of amines, exists as a rapidly interconverting mixture of isomers. Thus this sort of stereoisomerism is an extension of the isomerism encountered in ordinary organic and other main group compounds. The main new issues introduced by binding of such ligands to a metal center involve the creation of new possibilities for diastereoisomerism based on the stereochemistry of the metal center and the freezing out of stereocenter inversion on binding to a metal. The latter is particularly important for amines, which as free amines racemize rapidly by nitrogen inversion.
- or conformational isomerism involving five-membered chelate rings created when a multidentate ligand binds to a metal. This isomerism is often called chelate ring twist since individual rings can exhibit one of two conformations depending on how they twist on binding.
A summary of these forms of isomerism is given in Figure \(\sf{\PageIndex{1}}\).
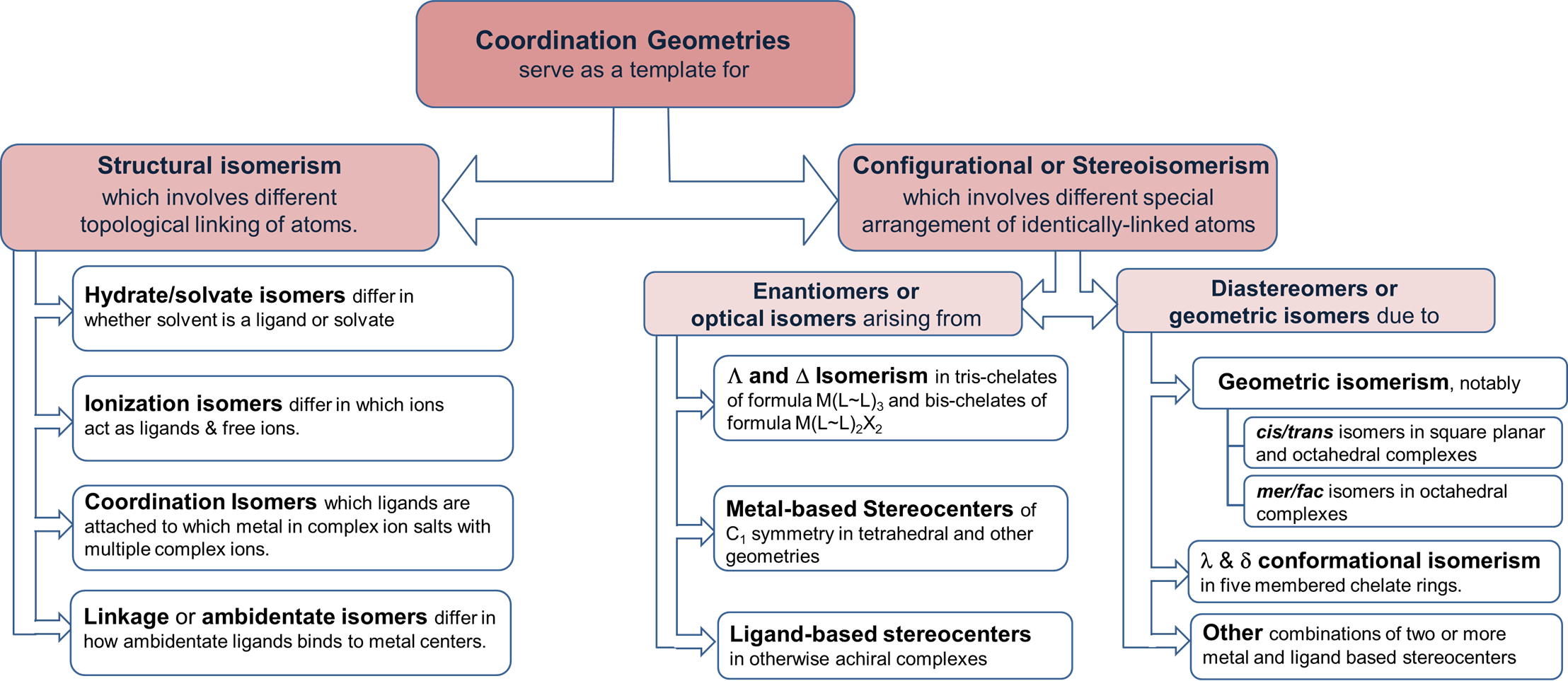
Structural isomers
Structural isomerism involves different topological linkages of atoms. Differences in atomic linkages distinctive to coordination chemistry involve the linkages between metals and ligands. The main variations are:
1. Hydrate/solvate isomerism
Solvate isomers differ in terms of whether a molecule acts as a ligand or whether it acts as a solvate by occupying a lattice site in the crystal. Among solvate isomers, the case in which water is the ligand or solvate is the best known. The resulting isomers are called hydrate isomers after the term for water acting as a solvate, hydrate. A well-known example that illustrates how solvate isomerism works is the series [CrClx(H2O)6-x]Cl3-x·xH2O, for which x = 0-2. The structures of the complex ions involved in this series are shown in Figure \(\sf{\PageIndex{2}}\).1
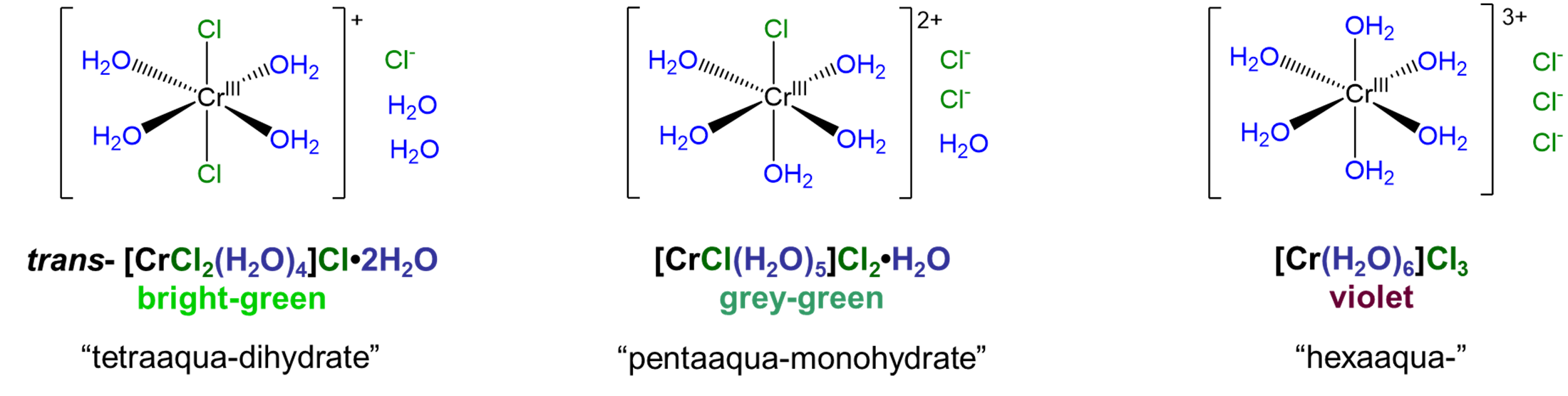
As can be seen from the compounds in Figure \(\sf{\PageIndex{2}}\), hydrate isomers differ both in terms of whether water acts as a ligand or hydrate and in terms of whether a potential counterion acts as a counterion or ligand. Thus, in trans-[CrCl2(H2O)4]Cl·2H2O two chlorides act as chloro ligands and four waters as aqua ligands while in [CrCl(H2O)5]Cl2·H2O five water molecules act as aqua ligands while only one chloride acts as a chloro ligand. In this way, solvate isomers simply represent cases in which two or more of the possible permutations for metal ligand binding among a set of solvent and counterion molecules are stable.
2. Ionization isomerism
In ionization isomerism there are two or more potential ions that can act as ligands. The ionization isomers differ in terms of which of these ions act as counterions and which act as ligands. Consider, for instance, the complexes shown in Figure \(\sf{\PageIndex{3}}\). These complexes differ in terms of whether the chloride or sulfate acts as a ligand, with the other acting as a counterion.
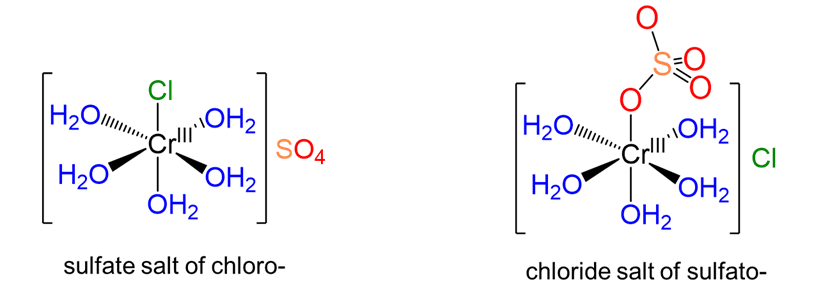
3. Coordination isomerism
Coordination isomers exist in compounds containing two or more complexes, each of which possesses a different set of ligands that can in principle be swapped with a ligand of the other complex. An example involves [CoIII(NH3)6][CrIII(ox)3], depicted in Figure \(\sf{\PageIndex{4A}}\).1 Coordination isomers of this complex involve swapping the ammine ligands around the Co3+ center for oxalato ligands surrounding the Cr3+ center. For instance, swapping all the ammine and oxalato ligands between the metal centers gives the coordination isomer [CrIII(NH3)6][CoIII(ox)3] shown in Figure \(\sf{\PageIndex{4B}}\).
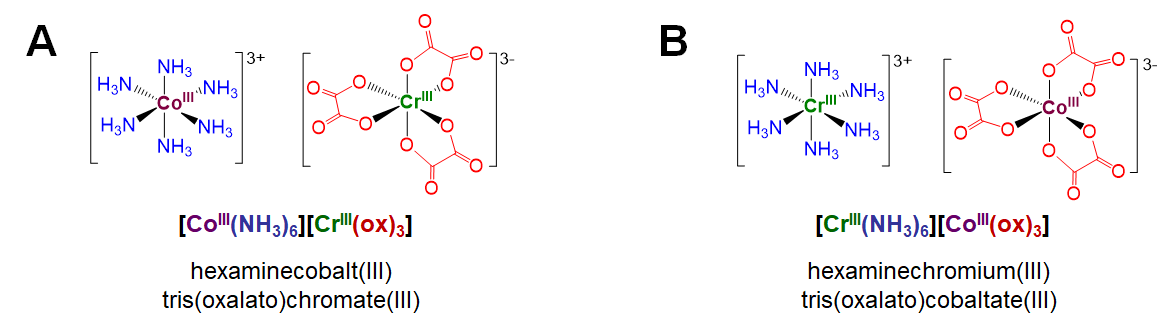
As classifications, hydrate/solvate, ionization, and coordination isomerism represent permutations of ordinary structure patterns for solvates, salts, and coordination complexes, respectively. As a result these forms of isomerism are rarely used as independent conceptual frameworks when thinking and talking about the structure of coordination compounds. Not so the final type of structural isomerism, linkage isomerism. That is because linkage isomerism has to do with the special capacity of ambidentate ligands to bind metals in multiple ways.
4. Linkage or ambidentate isomerism
Linkage or ambidentate isomers differ in how one or more ambidentate ligands bind to metal centers in a complex. The classic example dating from the work of Jørgensen and Werner is given in Scheme \(\sf{\PageIndex{I}}\).
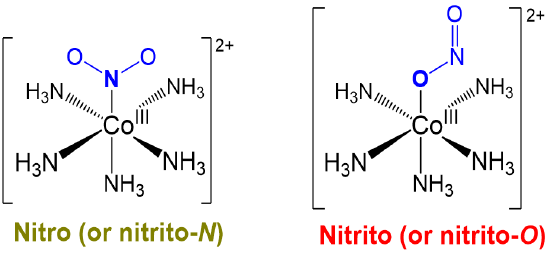
Just as alkenes exist as E and Z isomers, compounds possessing ambidentate ligands exist as one among the possible linkage isomers. As such, when working with ambidentate ligands the particular linkage isomer formed should be determined experimentally and considered when interpreting the complex's chemical and physical behavior.
The main ambidentate ligands which give rise to linkage isomerism are
- cyanide, CN-
- thiocyanate, SCN-, and the O and Se analogues, OCN- and SeCN-
- nitrite, NO2-
- sulfite, SO3-
- nitrosyl, NO
Although ambidentate ligands can bind metals in multiple ways, most exhibit a preferred binding mode (i.e., prefer to bind metal centers in one of the possible ways). For instance, cyanide almost always binds through its carbon atom and thiocyanate almost always binds through its nitrogen (\(\mu\)-N). However, the other binding mode can sometimes be formed kinetically or by using conditions that particularly favor its formation. Thus thiocyanate forms M-SCN- linkages in the presence of exceptionally soft metal centers or in hard polar solvents (in which Lewis acid groups can stablize the terminal nitrogen of a bound thiocyanate ligand).
Ambidentate ligands are of significant research interest because many don't just bind to metal centers in two ways; the linkage isomers sometimes have significantly different physical properties. In addition, the possibility of two binding modes introduces the possibility of exploiting linkage isomerism to take advantage of some of these ligands:
- different structural chemistry in different coordination modes. In mononuclear complexes the coordination mode influences which side of the ligand faces away from the complex and might be susceptible to stabilization by interaction with solvent. Additionally, the orientation of the ligand relative to the metal center might differ between one coordination mode and another. For instance, as predicted from the minor contributor to its resonance structure, thiocyanate binds nonlinearly via its S atom and linearly via its N (Figure \(\sf{\PageIndex{5}}\)). Because of this the apparent steric bulk of the ligand around the metal center might differ between forms.
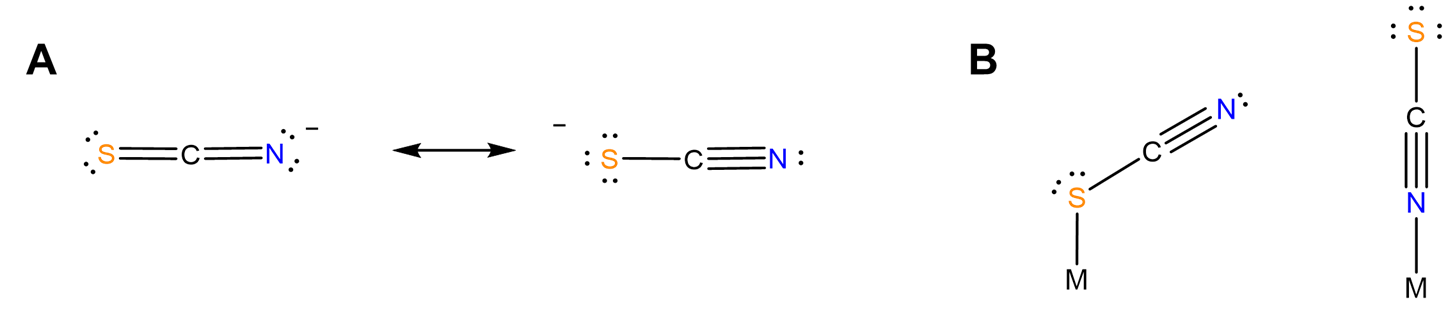
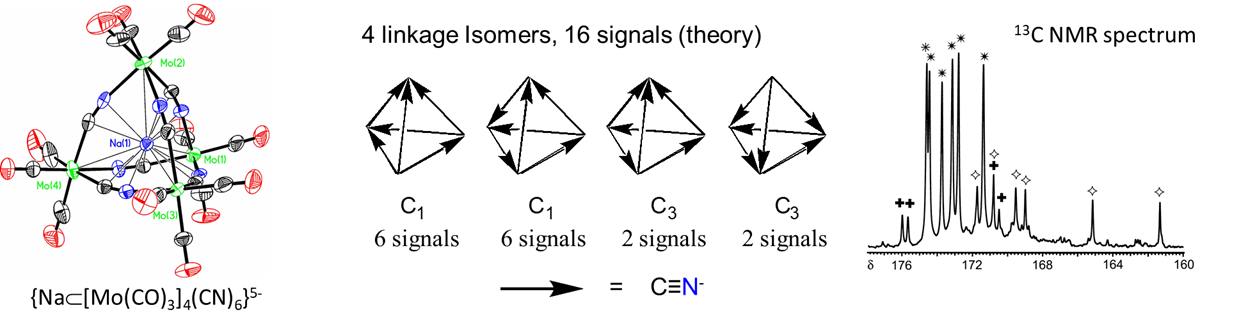
- bind two different metal centers at the same time, linking them together. Perhaps the best-known examples involve thiocyanate and cyanide. The latter forms linkages of the type M-C≡N-M'. In the dye Prussian blue these take the form FeII-C≡N-FeIII. An example from the author's graduate research involved tetrahedral clusters containing four metal atoms linked by six cyano ligands, as shown in Figure \(\sf{\PageIndex{6}}\).
- can be induced to change from one binding mode to another in response to a stimulus. The classic example involves the light-driven transformation of the thermodynamically more stable yellow nitro complex of pentamminecobalt(III), [Co(NH3)5NO2]2+ to the less stable red O-nitrito complex, [Co(NH3)5ONO]2+. Less stable cyanometallate coordination networks like those in the red K{FeII[CrIII(CN)6]} transform into the more stable green K{FeII[CrIII(NC)6]} form on heating, as shown in Figure \(\sf{\PageIndex{7}}\).3
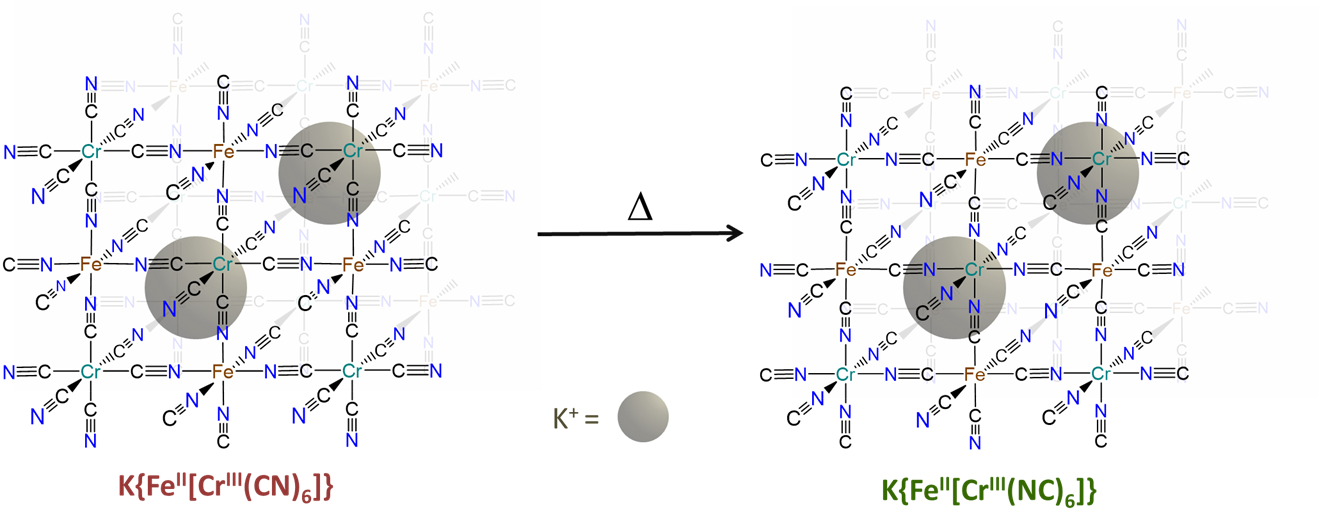
The hard-soft acid-base principle helps explain the preference of bridging ambidentate ligands for particular binding modes. How might the greater stability of the green K{FeII[CrIII(NC)6]} over red K{FeII[CrIII(CN)6]} be explained in terms of the hard and soft acid-base concept?
- Answer
-
The greater stability of K{FeII[CrIII(NC)6]} over K{FeII[CrIII(CN)6]} reflects the greater stability of the FeII-CN-CrIII linkages in the former over the FeII-NC-CrIII linkages in the latter. This is consistent with the preference for hard-hard and soft-soft Lewis acid-base interactions of the Hard-Soft Acid-Base Principle.
The FeII-CN-CrIII linkages are more stable because they possess bonds between
- the softer Lewis acid (FeII) and Lewis base (the C end of CN-)
- the harder Lewis acid (CrIII) and Lewis base (the N end of CN-)
In contrast, the FeII-NC-CrIII linkages in the less stable linkage isomer involve bonds between
- the softer base (the C end of CN-) and harder acid (CrIII)
- the harder base (the N end of CN-) and softer acid (FeII)
Stereoisomerism
Optical Isomerism/Chirality
Molecules of Dn, Cn, or C1 symmetry with only proper rotation axes (including E = C1) are chiral and exhibit optical isomerism. As described in Figure \(\sf{\PageIndex{1}}\), the main sources of such optical isomerism in coordination chemistry are:
-
Chirality inherent to an organic or main group ligand.
This type of isomerism is just an extension of the sort described in undergraduate organic texts and consequently does not merit separate discussion here, other than to note that some forms of optical isomerism which are of little importance in organic chemistry lead to optical activity in coordination compounds. In particular, the nitrogen inversion process which serves to rapidly racemize chiral amines is frozen out on formation of a metal-ligand bond. Because of this chiral amine, ligands bound to a metal form non-interconvertible R and S enantiomers, as shown in Figure \(\sf{\PageIndex{8}}\).
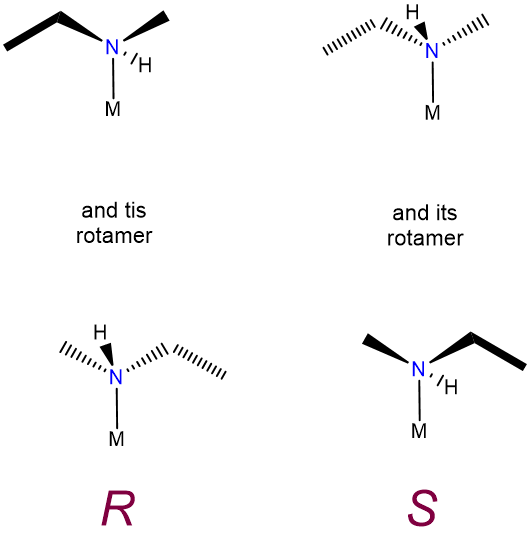
-
Chirality arising from the symmetry of ligands about a metal center.
The two common situations through which such chirality arises involve:
-
Chirality at a tetrahedral metal center surrounded by four different ligand attachment points.
Such cases are often referred to as MABCD or Mabcd where M stands for the metal and a, b, c, and d the four different ligand attachment points. An example of such a complex is given in Figure \(\sf{\PageIndex{9A}}\). The chirality of such complexes is analogous to the chirality arising from a tetrahedral carbon stereocenter. There are two caveats, though. First, it is not enough to have a four-coordinate complex; the metal must possess tetrahedral symmetry since, as shown in Figure \(\sf{\PageIndex{9B}}\), square planar M complexes with four different ligands are identical to their mirror images. Second, such chirality is most easily realized using macrocyclic ligands like proteins. Metal ligand bonds involving sterically unhindered monodentate complexes like that in the example of Figure \(\sf{\PageIndex{9A}}\) are in general weaker and more flexible than analogous carbon-carbon bonds. Consequently, in such cases it is likely that the enantiomers would interconvert through a fluxional process, making their resolution difficult if not impossible.

-
\(\Lambda\) and \(\Delta\) isomerism at octahedral metal centers surrounded by two or three chelating ligands.
Specifically,
- Octahedral tris-chelates of formula M(L~L)3 exhibit D3 symmetry.
- cis-octahedral bis-chelates of formula M(L~L)2XY exhibit C2 or C1 symmetry: C2 if X = Y and C1 if X \(\neq\) Y.
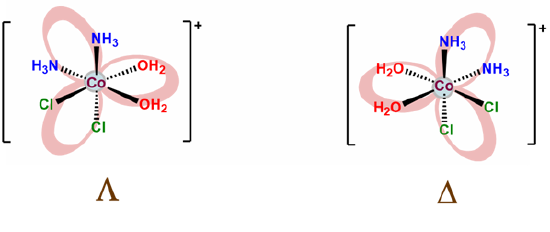
As shown in Figure \(\sf{\PageIndex{10A}}\), octahedral tris-chelates like [V(ox)3]3- are chiral and can exist as nonsuperimposable \(\Lambda\) and \(\Delta\) enantiomers. The chirality of these tris-chelates is analogous to that of pinwheels. As shown in Figure \(\sf{\PageIndex{10B}}\), when looking directly at the head of any individual pinwheel from above, the blades will be angled from back to front going around the pinwheel in either the clockwise or counterclockwise direction. As shown in Figure \(\sf{\PageIndex{10C}}\), the case for which the blades are angled in the clockwise direction is analogous to the \(\Lambda\) enantiomer and the case when they are angled in the counterclockwise direction the \(\Delta\).
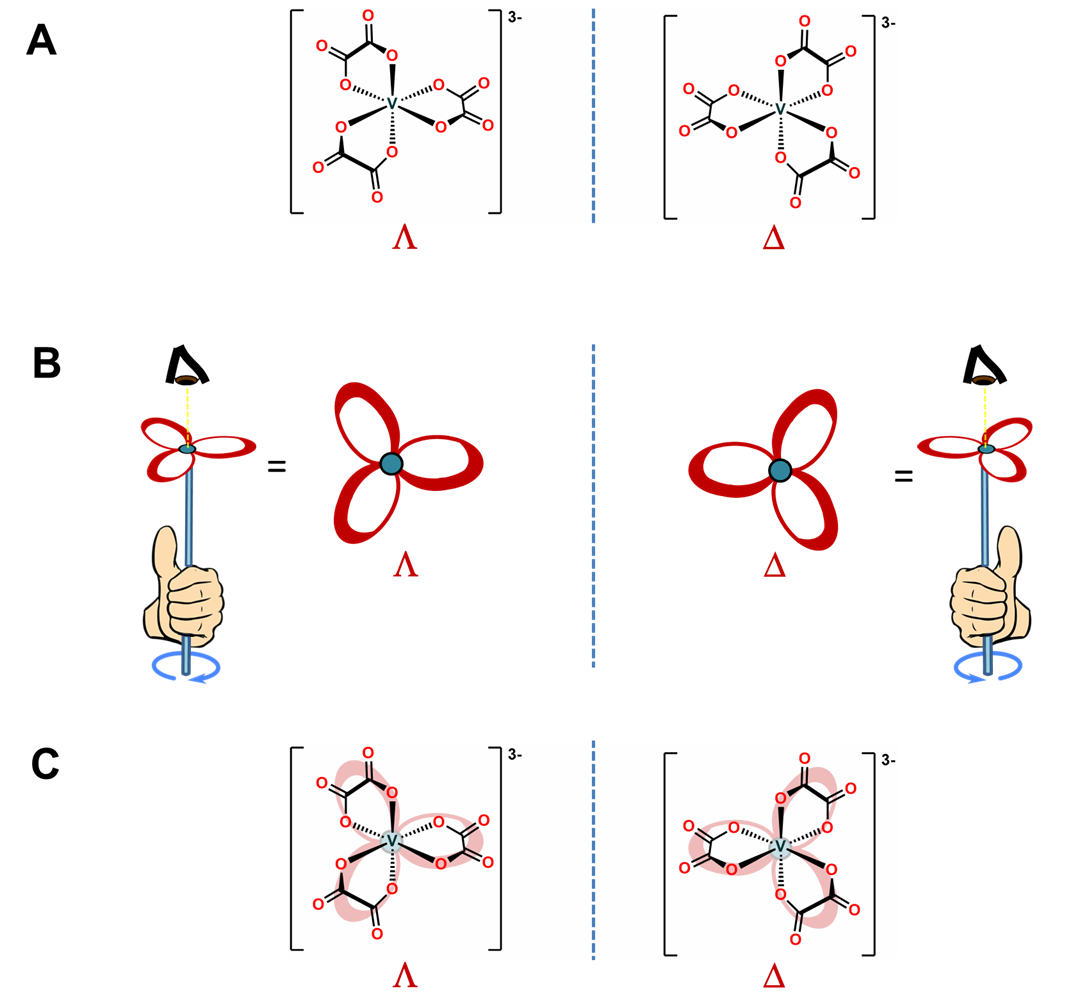
The \(\Lambda\) and \(\Delta\) chirality in octahedral bis-chelates is analogous to that in the tris-chelates except this time the third chelating ligand is replaced by an arbitrary pair of ligands. This lowers the symmetry of the complex to either C2 or C1, as shown for the C2 complex [CoCl2(en)2]+ in Figure \(\sf{\PageIndex{11A}}\). In either case the result is that such complexes exist as \(\Lambda\) and \(\Delta\) enantiomers analogous to those in the metal tris-chelates, as shown in Figure \(\sf{\PageIndex{11B}}\).
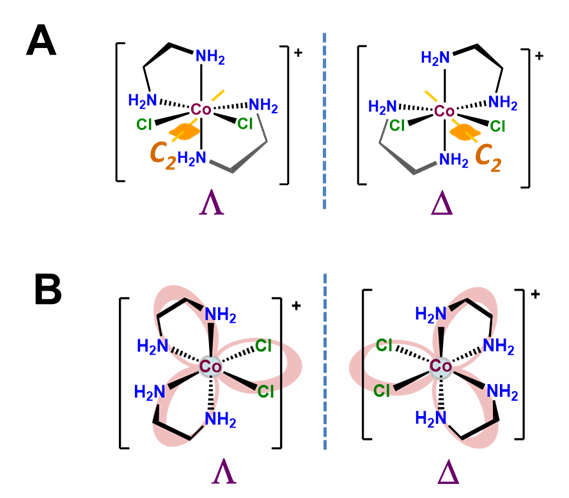
Octahedral complexes containing ligands with denticities of four or more also exhibit \(\Lambda\) and \(\Delta\) chirality; it is just that in such cases the bound ligand defines multiple rings within the complex that can be defined as existing in either \(\Lambda\) or \(\Delta\) orientations relative to each other. The procedure for making these assignments is beyond the scope of most introductory inorganic courses but the result is that such complexes are designated as \(\Lambda\Lambda\), \(\Delta\Delta\), \(\Delta\Lambda\), \(\Delta\Delta\Delta\), etc., depending on the number of relationships involving the rings defined by the bound ligand. Interested readers should consult reference 4 for more details.
Circular dichroism may be used to characterize optically active metal complexes.
At the present the most definitive way to determine the absolute configuration of an optically active coordination compound is to determine its 3D molecular structure using single crystal X-ray crystallography.5 However, as that is not always possible or convenient, the optical activity of coordination complexes is also commonly studied using circular dichroism (CD) spectroscopy. CD spectroscopy is used because, unlike most chiral organics, optically active coordination complexes possess low-energy electronic transitions that occur in the far UV and visible range. This means that it is often convenient to use the ability of a complex to refract and absorb different circular polarizations of light to derive information about both the configuration of an optically active complex and its electronic structure. The focus of this section will be to explain how the determination of absolute configuration by circular dichroism and optical rotatory dispersion work, as well as the relationship of these techniques to the more ordinary sort of polarimetry used to measure optical rotation in organic systems. Only brief notes will be made about the instrumental and electronic structure applications of these techniques since the electronic spectra of metal complexes will be discussed in Chapter 11: Coordination Chemistry III - Electronic Spectra and the instrumental aspects of CD are well-treated elsewhere.
Both polarimetry and circular dichroism spectroscopy are grounded in the recognition that plane polarized light is equivalent to a superposition of left and right circularly polarized light, as shown in Figure \(\sf{\PageIndex{12}}\).
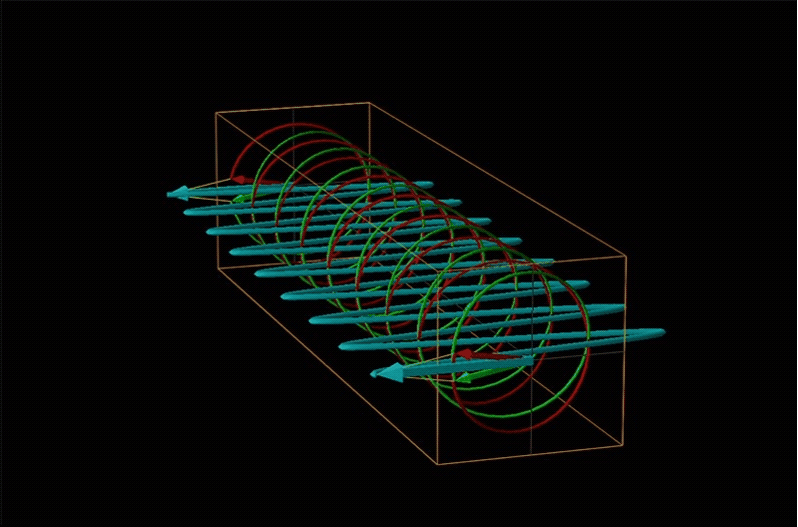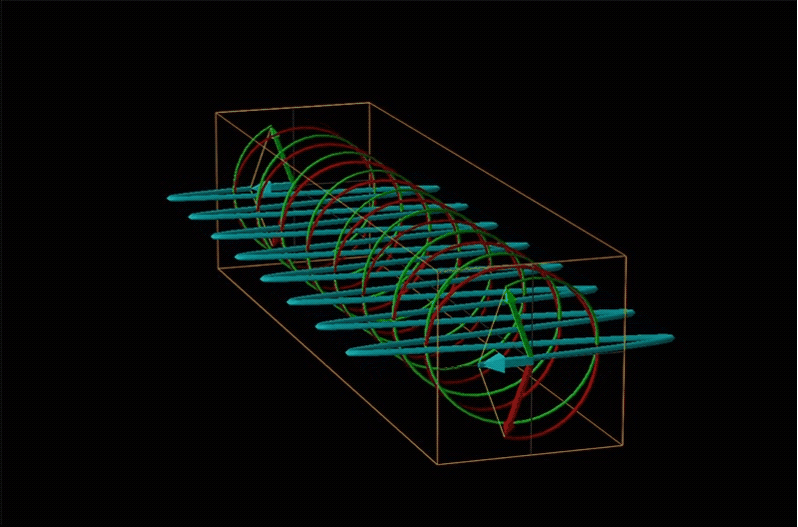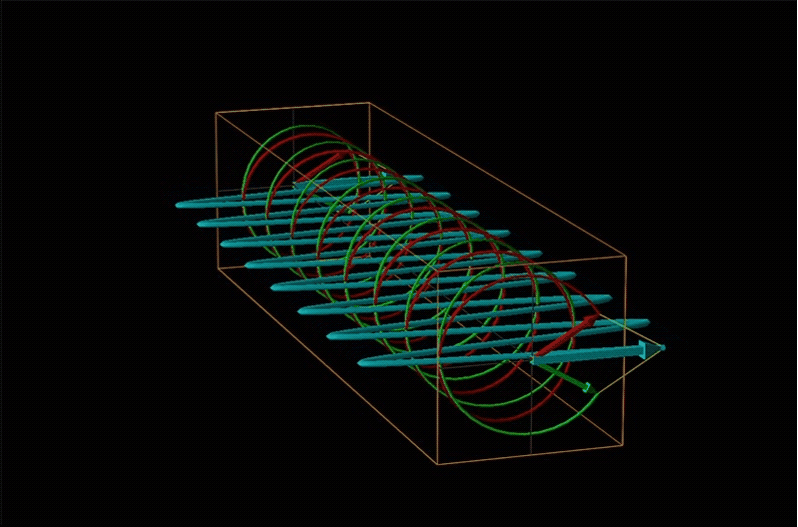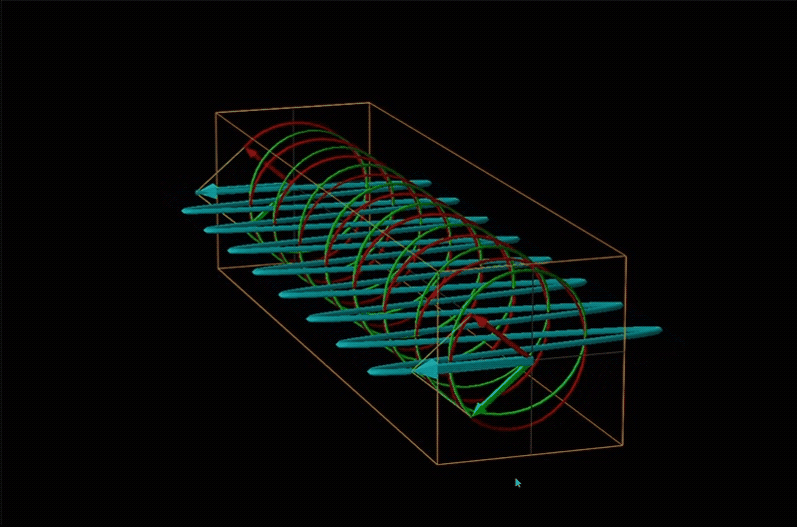

When plane polarized light passes through a chiral medium, its left and right circularly polarized components move at different rates (i.e., have different indices of refraction). This causes the plane of polarization to rotate in the direction of the faster component according to the relationship
\[\sf{\alpha ~=~\dfrac{n_l~-~n_r}{\lambda}} \nonumber \]
where \(\alpha\) is the angle of rotation, \(\lambda\) the light's wavelength, and nl and nr the refractive indices experienced by left and right circularly polarized light.
An example of such a rotation is shown in Figure \(\sf{\PageIndex{13}}\).
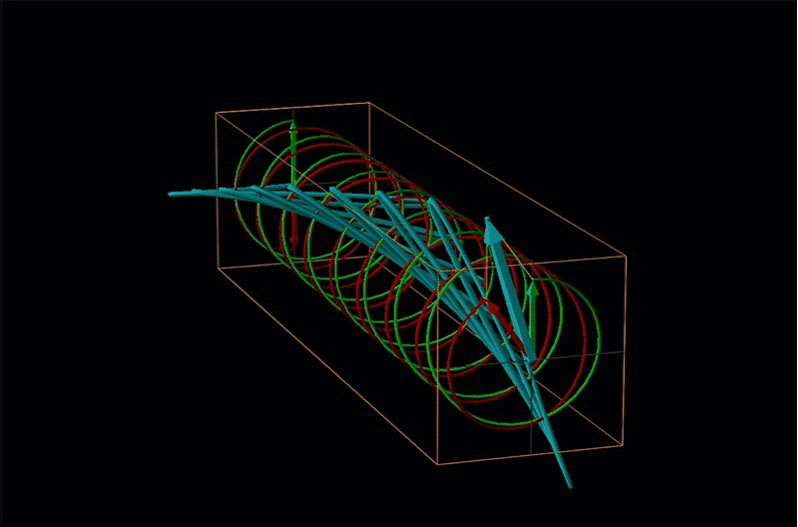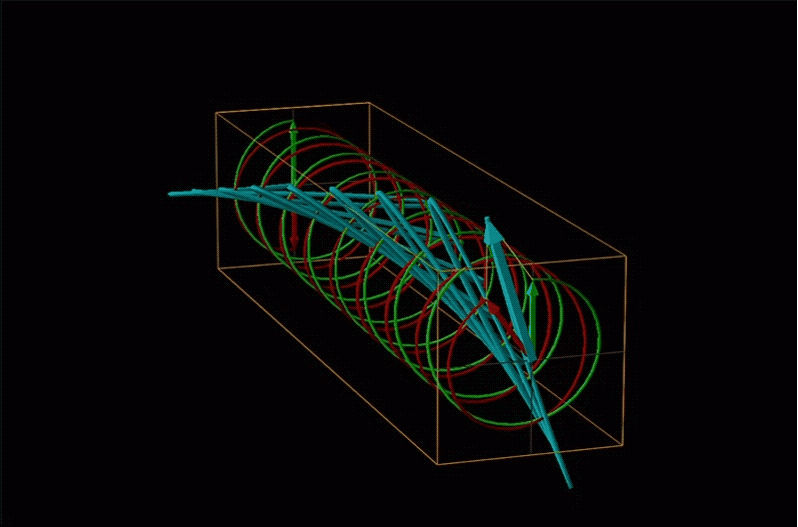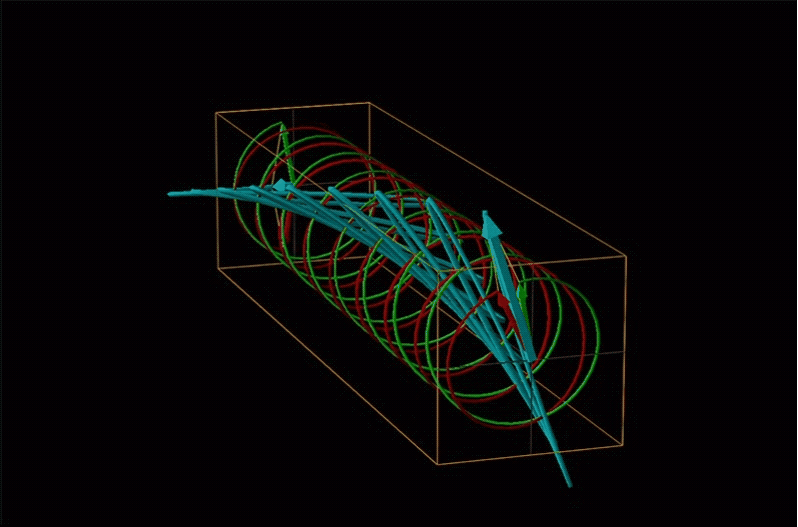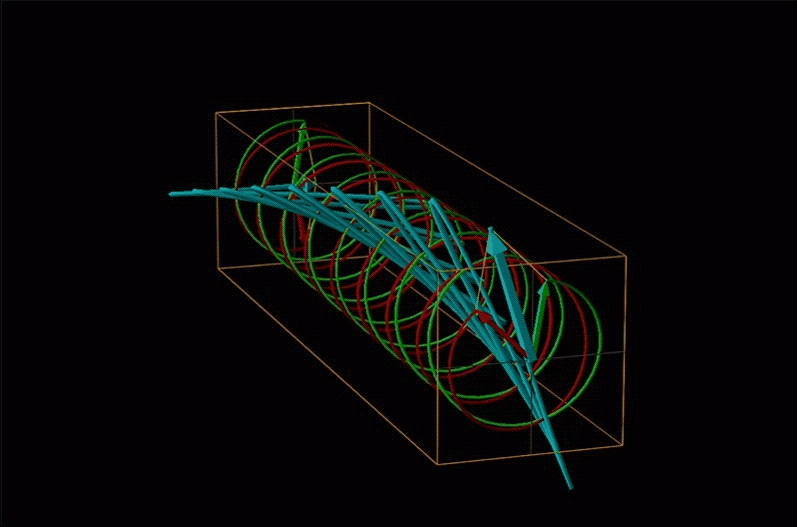

Chemists typically call this rotation of light by a chiral medium optical rotation. In organic chemistry it is common to measure the optical rotation at the sodium D wavelength of 589.29 nm, a much longer wavelength than most organics are able to absorb. Because of this the optical rotations commonly measured by organic chemists are largely independent of absorption and mainly serve as a characteristic physical property similar to melting points or are used to establish the purity of a mixture of enantiomers. The sort of spectroscopic data used to characterize chiral coordination compounds more commonly makes use of the relationship between absorption and optical rotation.
In coordination chemistry the wavelength-dependence of optical rotation is used to discern information about compounds' electronic spectra. This measurement of the wavelength dependence of optical rotation is called optical rotatory dispersion (ORD) and the resulting plots are called optical rotatory dispersion or ORD spectra or curves. Such ORD curves are useful for characterizing the chiral environment in a coordination complex because the ORD curves exhibit a characteristic shape. This characteristic shape is because according to the Cotton Effect, the optical rotation changes sign at the absorption maximum of a chromophore in the compound. For one configuration the rotation will go from negative to positive with increasing wavelength and is called a positive cotton effect; for the other configuration the rotation will go from positive to negative or exhibit a negative cotton effect. This behavior is summarized in the top two curves of Figure \(\sf{\PageIndex{14}}\).
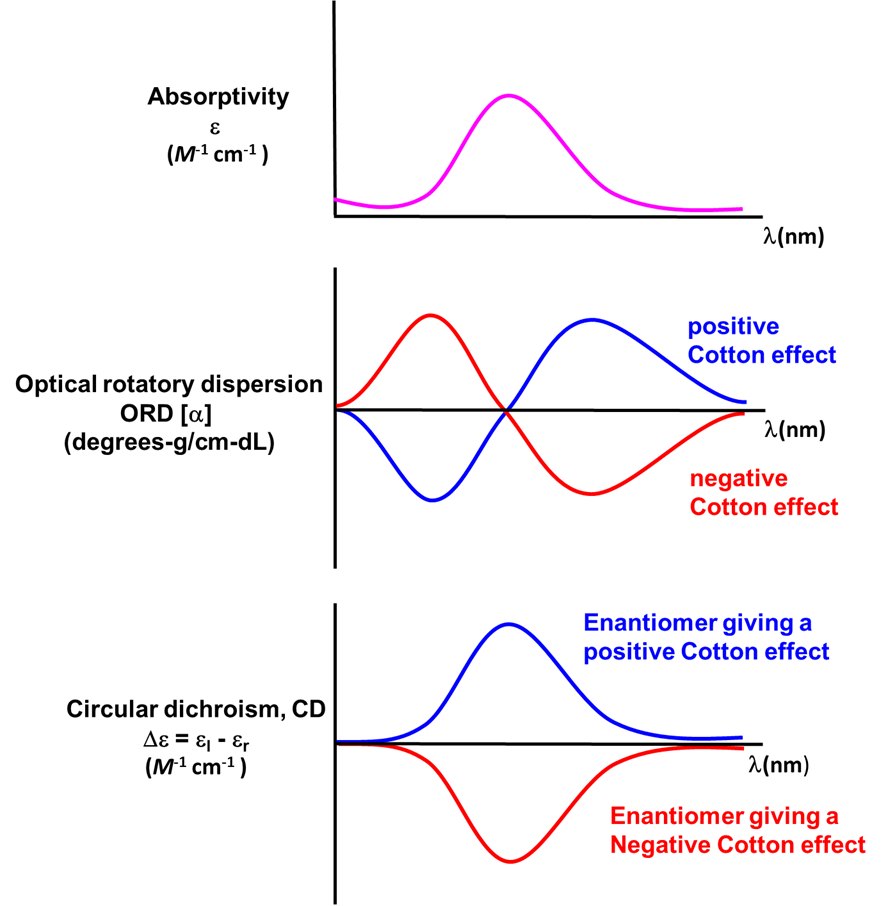
A technique used even more often than ORD is circular dichroism (CD), represented by the lowest spectrum in Figure \(\sf{\PageIndex{14}}\). Circular dichroism arises from the differential absorption of left and right circularly polarized light by a chiral compound. This gives elliptically polarized light as shown in Figure \(\sf{\PageIndex{15}}\).
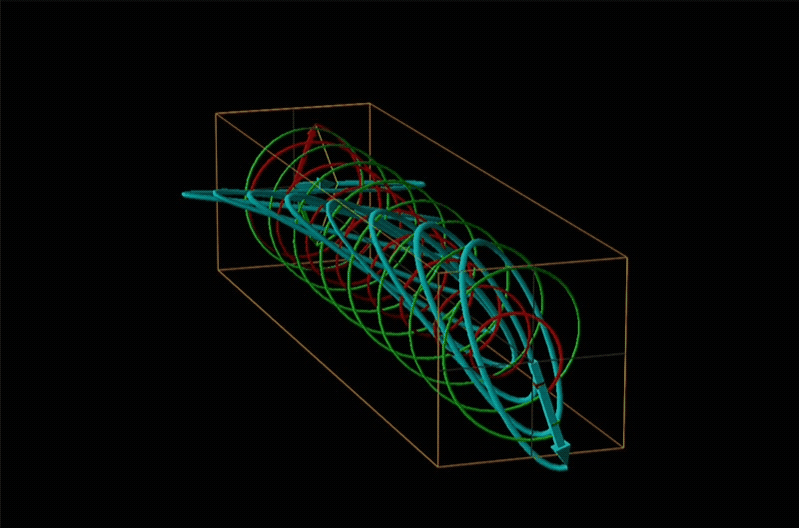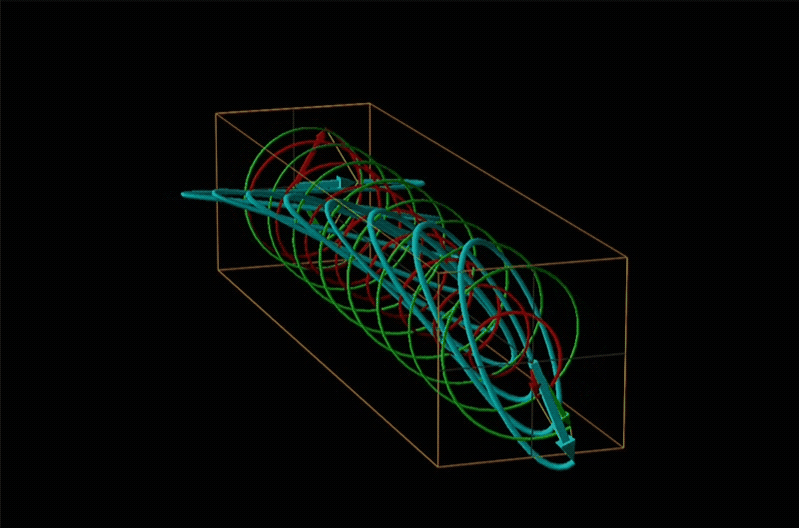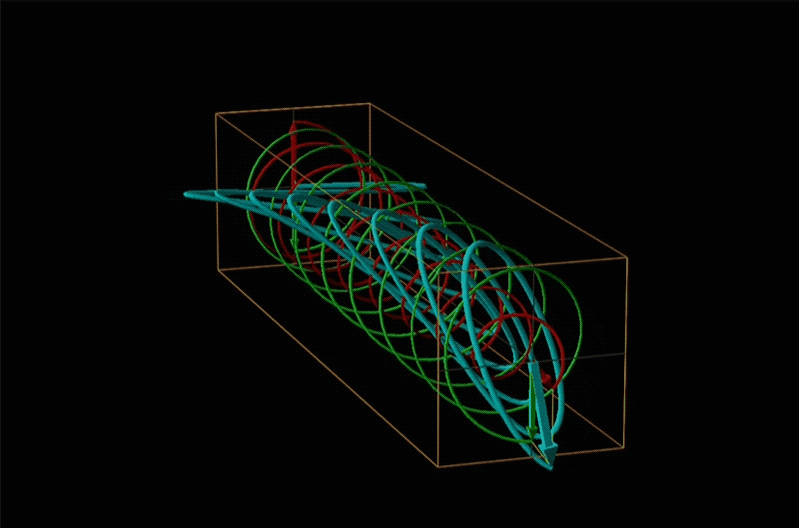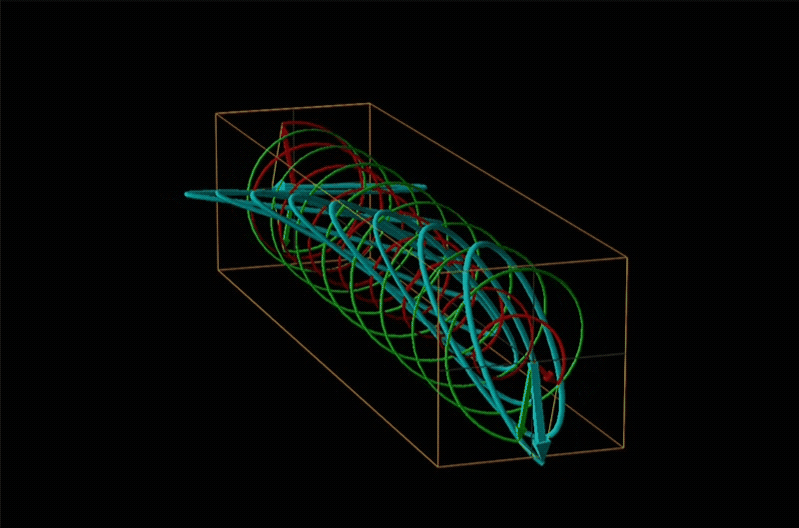

In circular dichroism (CD) spectroscopy a sample is irradiated with polarized light resulting in the transmission of elliptically polarized light due to differential refraction and absorption of the polarized light's left and right circularly polarized components. For achiral molecules the handedness doesn't affect absorbance, but for chiral molecules, which chiral ground and excited states the handedness of an EM wave affects can determine how readily that wave can distort the chiral ground state into the chiral excited one. For this reason chiral molecules absorb left and right circularly polarized light differently.
In CD spectroscopy the magnitudes of the left and right circularly polarized components of light that is transmitted by the sample are measured and used to determine how much light of each was absorbed (just as in regular absorbance spectroscopy). The difference in absorption between left and right circularly polarized light constitutes the primary signal in CD spectroscopy. More specifically, circular dichroism spectra (CD spectra) show the difference in extinction coefficients for left and right circularly polarized light, \(\Delta \epsilon\), as a function of wavelength, where
\[\sf{\Delta \epsilon\ ~=~ \epsilon_l ~-~\epsilon_r} \nonumber \]
where \(\epsilon_\sf{l}\) and \(\epsilon_\sf{r}\) are the extinction coefficients observed with left and right circularly polarized light, respectively.
As with ORD spectra, the signs of the features in CD spectra like that of Δ–[Co(en)3]Cl3 given in Figure \(\sf{\PageIndex{16}}\) are enantiomer-dependent. As illustrated in the lower spectrum in Figure \(\sf{\PageIndex{14}}\) , the CD spectra of enantiomers mirror one another. Because of this difference in behavior it is possible in principle to determine the absolute configuration of a complex from its CD spectrum.
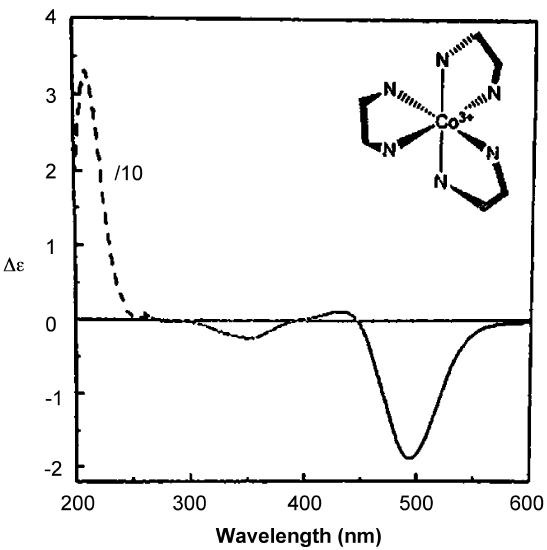
There are several ways that ORD and CD spectra can be useful for determining the absolute configuration of a chiral complex.
- First, the sign of the Cotton effect and peaks in CD spectra exhibited by a given absolute configuration is often consistent across a series of compounds. Thus if a new member of the series is isolated, its configuration can be determined based on which enantiomer has the same Cotton effect. For instance, if both the \(\Lambda\) isomer of a metal diimine complex like [Ru(bpy)3]2+ exhibit a positive Cotton effect and a newly resolved metal diimine exhibits a negative Cotton effect it might reasonably be inferred that the newly-resolved complex is in the opposite or \(\Delta\) configuration.
- Second, for some systems the expected sign of the Cotton effect and CD peaks for each enantiomer may be predicted semi-empirically based on the spatial locations of substituents relative to the chromophore (the part of the molecule that changes electronic structure during the transition), although the details are beyond the scope of the present discussion.
- Consideration of interactions between multiple chromophores in a compound can be used to infer absolute configuration. Again, the details are beyond the scope of the present discussion. Interested readers are referred to reference 7 for details.
Common patterns of Diastereomerism
Geometric isomerism
Geometric isomerism involves differences in the geometric placement of atoms in a compound. In coordination chemistry, geometric isomerism involves differences in the relative placement of a set of ligands about a metal center. There are two main types:
cis and trans isomerism
This type of isomerism has to do with how two ligands are oriented relative to one another in a square planar or octahedral complex. As shown in Figure \(\sf{\PageIndex{17}}\), ligands that are next to one another with a L-M-L bond angle of 90\(^{\circ}\) are said to be cis; those on opposite sides of the metal with a L-M-L bond angle of 180\(^{\circ}\) are in the trans arrangement.
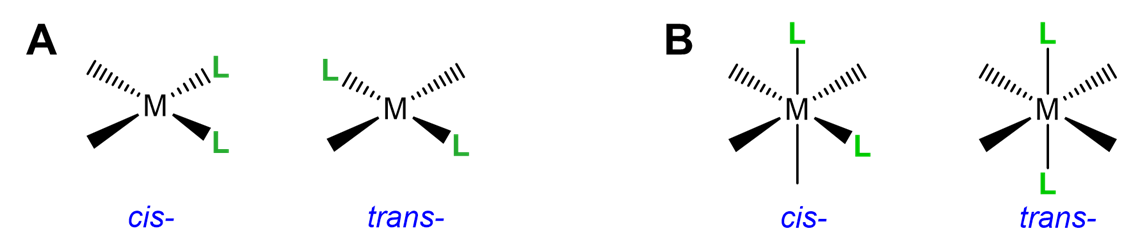
Simple cis and trans geometric isomers can be identified when there are two identical ligands (A) or chelating ligands with distinguishable attachment points (A~B) oriented about either a square planar or octahedral center. Examples are given in Figure \(\sf{\PageIndex{18}}\). Notice from the example given in Figure \(\sf{\PageIndex{18C}}\) that multidentate ligands have the potential to constrain complexes to adopt a particular geometry.

Slightly more involved examples involve perturbations of the simple cases above in which there are multiple distinguishable cis and/or trans relationships. Two square planar examples are given in Figure \(\sf{\PageIndex{19}}\).
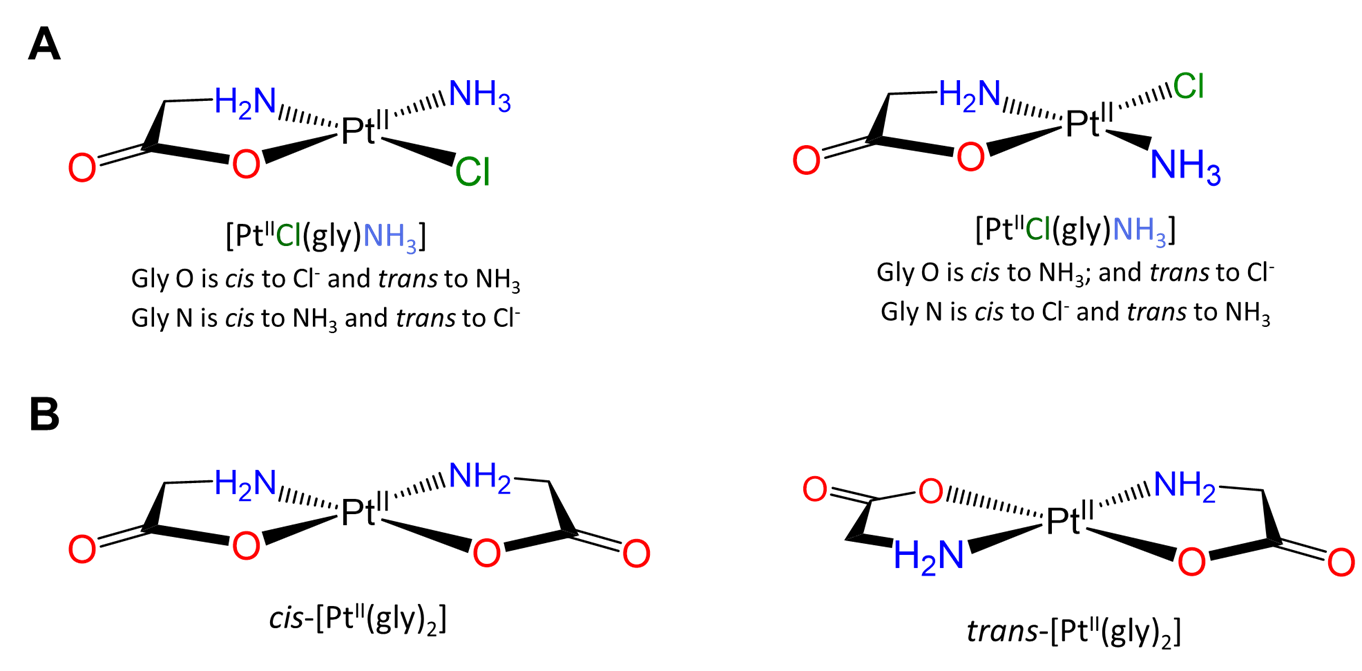
More complex examples of cis and trans relationships between ligands in octahedral complexes are given in the exercises that conclude this page, which also demonstrates how a systematic approach may be used to identify isomers.
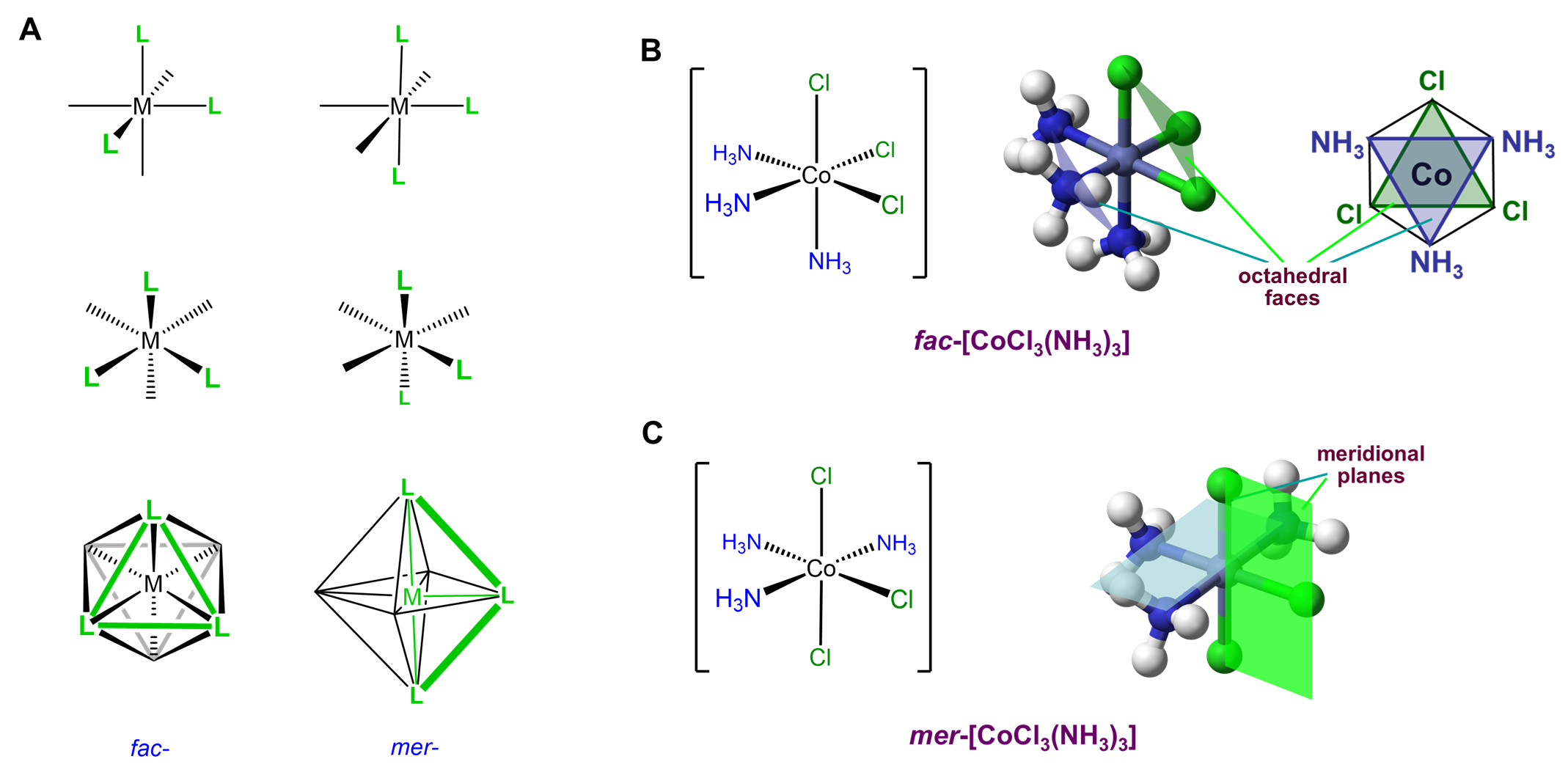
mer and fac isomerism
This type of isomerism has to do with how three ligands are oriented relative to one another in an octahedral complex. The arrangements are represented in Figure \(\sf{\PageIndex{20}}\).
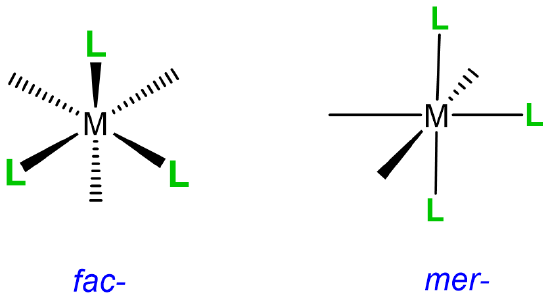
Since it can help to visualize the mer and fac geometry from multiple points of view, several representations are given in Figure \(\sf{\PageIndex{21}}\). As shown in Figure \(\sf{\PageIndex{21}}\), in fac or facial arrangements, the ligands occupy the same "face" of the octahedral coordination sphere, while in the mer or meridional geometry the ligands form a T shape in the same plane or its "meridian."8
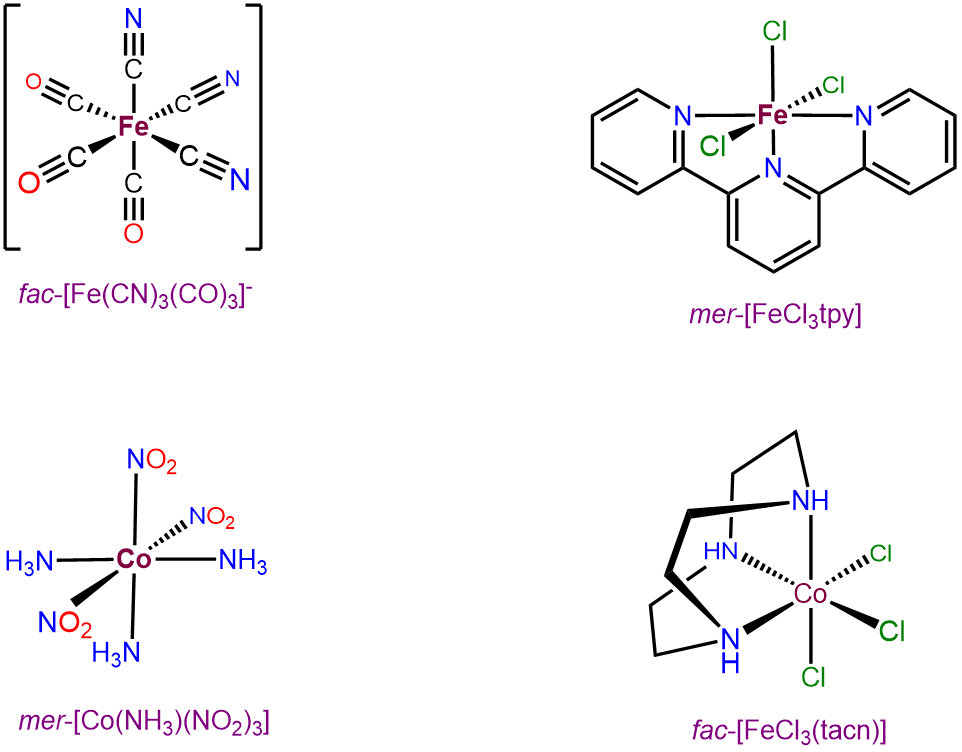
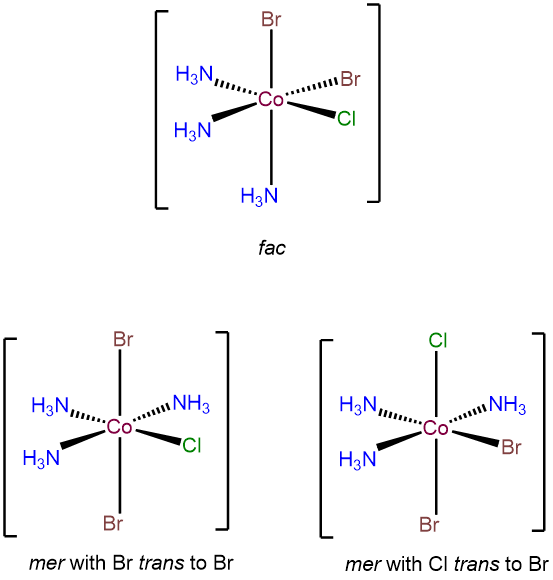
Octahedral complexes with three identical ligands oriented about an octahedral center can only exist in mer and fac arrangements. Consequently, such complexes can be designated as mer and fac isomers. Examples are given in Figure \(\sf{\PageIndex{22}}\).
Diastereomerism arising from multiple ligand-associated chiral centers
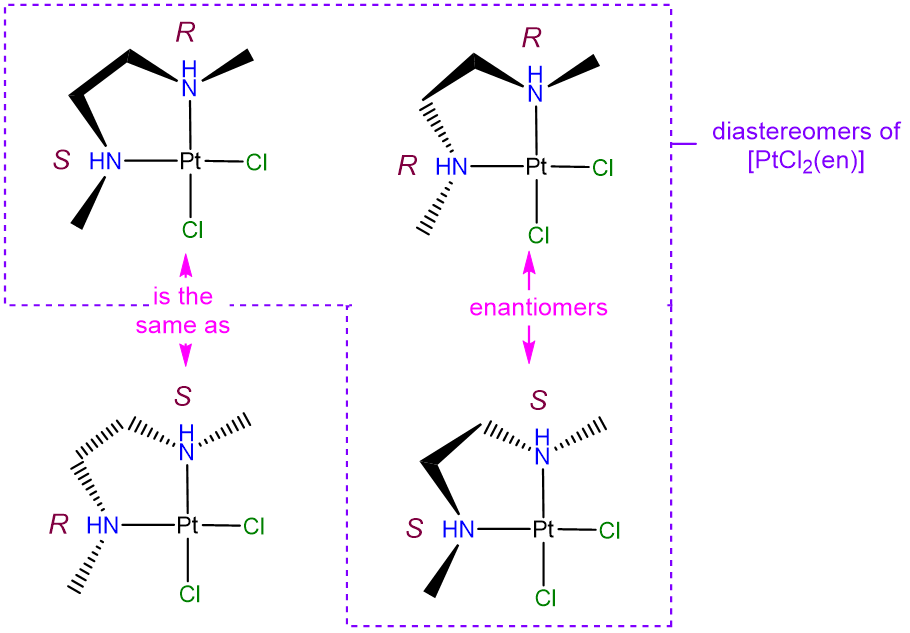
Diastereomerism can also arise when two or more chiral ligands bind to a metal center. Such cases typically give rise to a complex mixture of isomers, as shown by the example in Figure \(\sf{\PageIndex{23}}\). As may be seen from Figure \(\sf{\PageIndex{23}}\), the differences between these isomers can arise from both changes in the stereochemical configuration of the ligand and the relationship of particular ligand centers relative to one another. For instance, the leftmost two structures in Figure \(\sf{\PageIndex{23}}\) possess one R and S nitrogen center each but differ in whether the centers are oriented so that the R and S centers on the two ligands are trans or cis to one another.

Diastereomerism arising from \(\lambda\) and \(\delta\) ring conformation isomerism.
Chelate rings are formed when a chelating ligand binds a metal
As may also be seen from the structures in Figure \(\sf{\PageIndex{23}}\), when a multidentate ligand coordinates a metal, the ligand and metal center comprise one or more chelate rings. Examples of such chelate rings are shown in Figure \(\sf{\PageIndex{24}}\).

As may be inferred from the examples in Figure \(\sf{\PageIndex{24}}\), chelate rings may be of different sizes, although four, six, and especially five-membered rings are particularly common. Exactly which ring sizes will be more stable for a given system depends on the coordination geometry and, due to differences in M-L bond lengths, to a lesser degree on the metal. As a result, for octahedral and square planar complexes with 90\(^{\circ}\) L-M-L bond angles between cis ligands, five-membered rings tend to be especially stable (Figure \(\sf{\PageIndex{25}}\)).
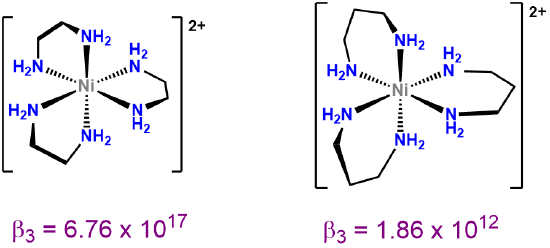
Not all metal chelates prefer to form five-membered rings. The steric requirements of chelate rings depend on both the preferred coordination geometry of the metal center and the stereochemistry of the ligand. Both of these effects are typically considered in terms of preferred L-M-L bond angles. From the perspective of the metal center, the preferred bond angle is determined by the coordination geometry. Octahedral and square planar metals prefer 90\(^{\circ}\) L-M-L bond amgles, trigonal bipyramidal systems 90 and 120\(^{\circ}\) L-M-L bond angles, and tetrahedral complexes 109.5\(^{\circ}\) L-M-L angles. The larger preferred bond angles in tetrahedral and trigonal bipyramidal systems often require the formation of larger six or seven-membered chelate rings for maximum stability. The size of the chelate ring actually formed between a metal and ligand is determined by the ligand's structure. As the contributor of all the atoms in the chelate ring but one, the ligand directly determines the chelate ring size. More subtly, ligands naturally prefer to coordinate metals at a particular L-M-L angle, called the bite angle, as shown in Figure \(\sf{\PageIndex{26A}}\). Ligands with bite angles corresponding to the ideal L-M-L angle for a metal's preferred geometry tend to form more stable complexes, although in turn ligand bite angles can cause metals with a weak coordination geometry preference to adopt the ligand's preferred geometry instead.10 As may be seen from the values in Figure \(\sf{\PageIndex{26B}}\), bite angles roughly increase with the size of the chelate ring formed but are also influenced by the types of structures used to connect the ligand's Lewis base sites. This facilitates the use of diphosphine ligands to tailor the structure and reactivity of phosphine-containing organometallic catalysts.

\(\lambda\) and \(\delta\) isomerism involves differences in the conformation of nonplanar five-membered chelate rings
As shown in Figure \(\sf{\PageIndex{27}}\), some chelate ring systems are planar while others are not.
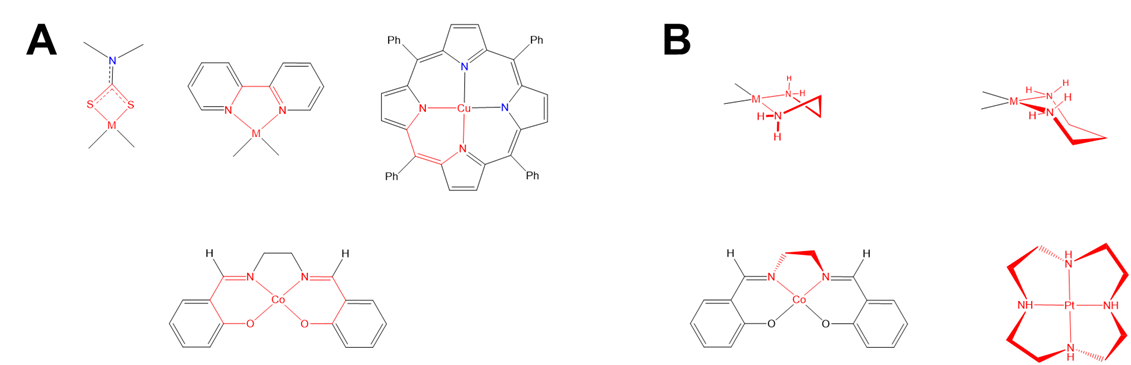
Among the nonplanar chelate ring systems are ligands like en and dppe, which contain tetrahedral C, N, O, P, and S atoms. Because these atoms create kinks in the chelate ring they introduce additional opportunities for diastereomerism due to differences in the chelate ring conformation, called ring twist. Ring twist in nonplanar systems has been most extensively explored for five-membered chelates like those formed by dppe and by en and other chelating amines. Unlike the more rigid four-membered chelate rings, five-membered chelates tend to be conformationally flexible, but not so conformationally flexible that their conformers are rapidly interconverting at room temperature (at least not when the rings are substituted to introduce additional steric strain). This balance between flexibility and rigidity enables some five-membered chelate rings to exist as mixtures of distinguishable conformational isomers at room temperature.
To understand the two most stable conformers that five-membered chelates rings tend to form, it is helpful to think of five-membered chelate rings as involving two components (Figure \(\sf{\PageIndex{28}}\)):
- a planar L-M-L group, where L are the atoms directly attached to the metal, M, and
- the remaining two ring atoms, E, which form a rigid E-E bar across the back of the chelate ring.
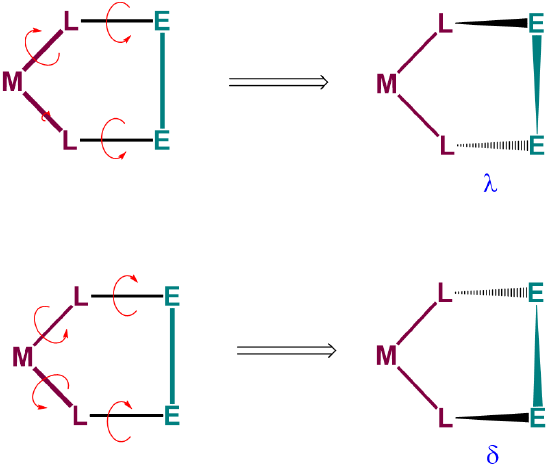
As can be seen from Figure \(\sf{\PageIndex{28}}\) , rotation about the M-L and L-E bonds causes twisting of the E-E bar relative to the L-M-L plane. The two most stable conformers produced by these motions are the \(\lambda\) or \(\delta\) conformations as shown in Figures \(\sf{\PageIndex{29}}\) and \(\sf{\PageIndex{29}}\).
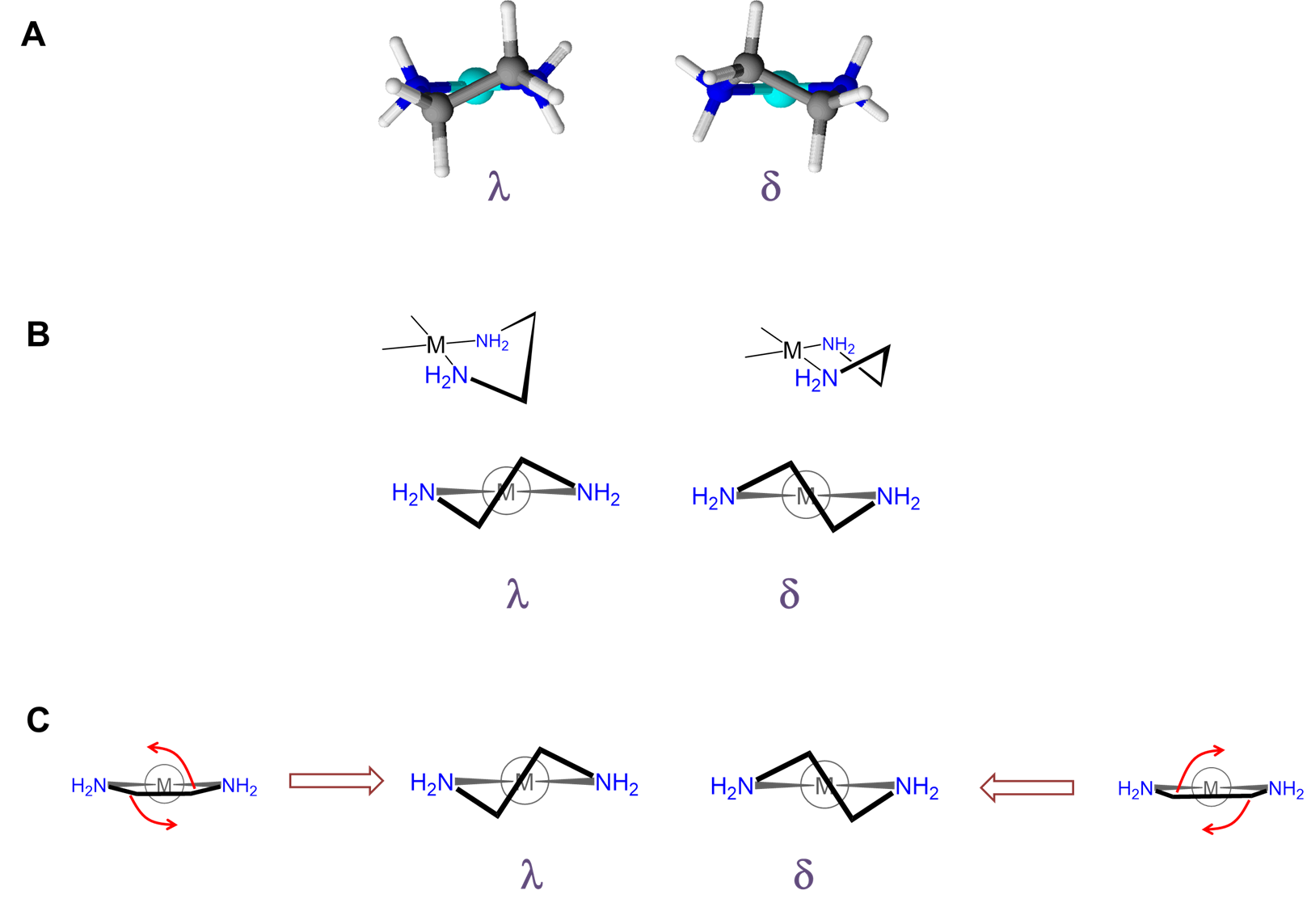
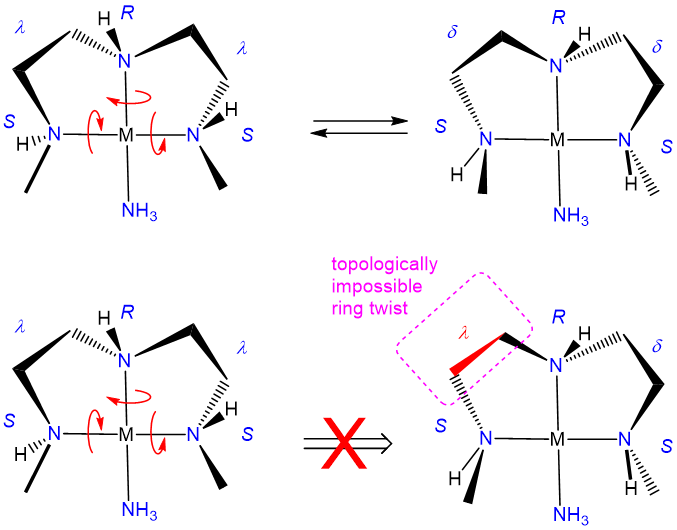
The relative stability of the \(\lambda\) and \(\delta\) conformers will depend on the configuration of any stereocenters present and steric factors. As with organic ring systems, steric effects tend to favor conformers in which bulky groups are placed in the less sterically strained equatorial positions while the configuration of the stereocenters present can serve to restrict the allowable ring twist conformations, as illustrated in Figure \(\sf{\PageIndex{30}}\). A detailed treatment of such systems is beyond the scope of this page. Interested readers are referred to reference 12 for more details.
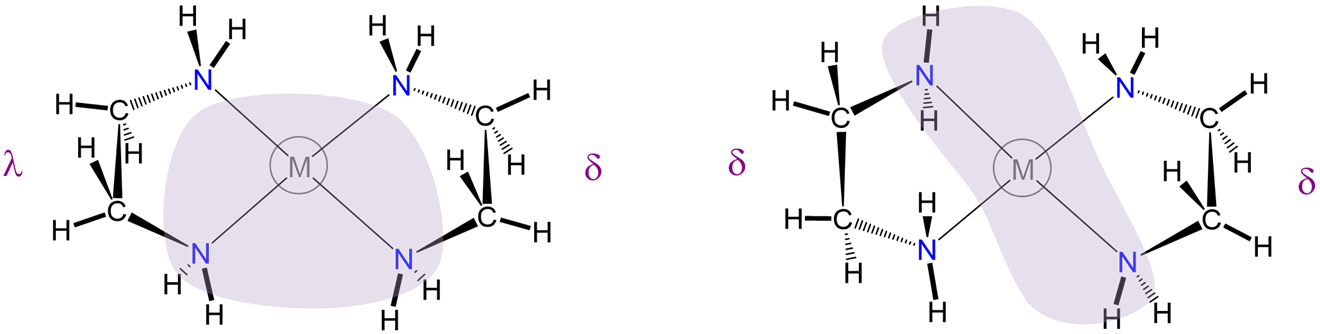
In closing, it should be noted that it might seem to be making much of small effects in pointing out that one source of diastereomerism in metal complexes involves the freezing out of chelate ring conformations. However, that would be to mistake the impacts that ring conformations can have on the steric accessibility of a coordination site and shaping the course of processes that might occur there. As illustrated in Figure \(\sf{\PageIndex{31}}\), a simple shift in the conformation of one ring in a square planar, pyramidal, or octahedral complex containing coplanar ethylene diamine ligands can exert a significant effect on the steric profile of the complex perpendicular to the MN4 square plane. Because of effects like these, ring conformation isomerism plays a role in the design of stereoselective transition metal catalysts.
Exercises
What type of isomers are
- [CoCl(NH3)5](NO3) and [Co(NH3)5(N-NO2)]Cl?
- [Co(NH3)5-CN-Ru(NH3)5]4+ and [Co(NH3)5-NC-Ru(NH3)5]4+
- [Cr(CN)5-CN-Co(NH3)5] and [Co(CN)5-CN-Cr(NH3)5]
- cis-[Mn(en)2(CN)2] and trans-[Mn(en)2(CN)2]
- Answer a.
-
Ionization isomers.
- Answer b.
-
Linkage isomers.
- Answer c.
-
Coordination isomers.
- Answer d.
-
Geometric isomers, specifically cis/trans isomers.
Many properties of transition metal complexes depend on the metal's oxidation state. For instance,
- octahedral complexes of CoII lose and gain ligands rapidly
- octahedral complexes of CoIII lose and gain ligands very slowly
- four-coordinate complexes are generally tetrahedral
- EXCEPT four-coordinate complexes of metals like PtII , PdII , RhI, and IrI, among others, are square planar
For this reason it is important to be able to estimate the formal oxidation state of a metal in a complex. Fortunately, this is easy to do if you remember
- The sum of all atoms' oxidation states will equal the overall charge on the complex
- When determining the metal's oxidation state, the ligands can be treated as having an oxidation state equal to their charge - i.e., the charge they possess in the form in which they coordinate the metal - so if they need to lose a proton to bind, don't forget to account for that.
Given the above, estimate the oxidation state of the metal in the following real and hypothetical complexes.
- Na4[Fe(CN)6]
- [Cu(phen)2]BF4
- [PtF4(NH3)2]
- [Ni(en)2]SO4
- Co(acac)3
- [MnCl(O)(salen)]
- Answer for Na4[Fe(CN)6].
-
This contains [Fe(CN)6]4-; so O.S.Fe + 6 x (-1) (for CN-) = -4 (the complex's charge) so O.S.Fe = +2 or Fe2+.
- Answer for [Cu(phen)2]BF4.
-
Since tetrafluoroborate is a monoanion, the complex is [Cu(phen)2]+ so O.S.Cu + 0 x 2 (for phen) = +1 (the complex's charge) so O.S.Cu = +1 or Cu+.
- Answer for [PtF4(NH3)2].
-
O.S.Pt + 4 x (-1) (for F-) + 0 x 2 (for NH3) = +0 (the complex's charge) so O.S.Pt = +4 or Pt4+.
- Answer [Ni(en)2]SO4.
-
The complex is [Ni(en)2]+ so O.S.Ni + 0 x 2 (for en) = +2 (the complex's charge) so O.S.Ni = +2 or Ni2+.
- Answer Co(acac)3.
-
O.S.Co + 3 x (-1) (for acac; see table 9.2.2) = +0 (the complex's charge) so O.S.Co = +3 or Co3+.
- Answer [MnCl(O)(salen)].
-
O.S.Mn + 1 x (-1) (for Cl-) + 1 x (-2)(for oxo) + 1 x (-2) (for salen; see table 9.2.2) = +0 (the complex's charge) so O.S.Mn = +5 or Mn5+.
Draw structures that match the descriptions given, assuming that
- complexes in which the metal has a coordination number of six are octahedral
- complexes in which the metal has a coordination number of five are trigonal bipyramidal
- complexes in which PtII , PdII , or RhI, or IrI have a coordination number of four are square planar
- other complexes in which the metal has a coordination number of four will be tetrahedral
- mer-triammineaqua-trans-dichlorocobalt(III) ion
- \(\Delta\)-diaminebis(oxalato)manganate(III)
- [CoCl4]2-
- trans-diamminebis(ethylenediamine)Nickel(2+) tetracyanopalladate(2-)
- \(\Lambda\)-bis(ethylenediamine)cobalt(III)- μ-amido μ-hydroxo-\(\Delta\)-bis(ethylenediamine)cobalt(III)
- Answer a. mer-triammineaqua-trans-dichlorocobalt(III) ion.
-
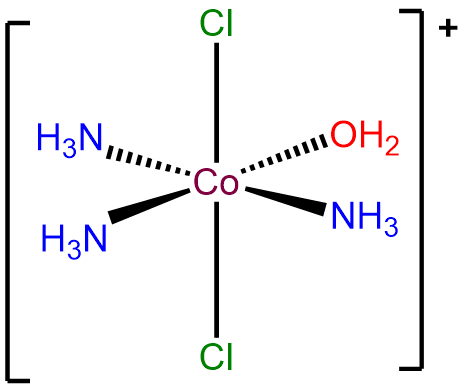
- Answer b. \(\Delta\)-diaminebis(oxalato)manganate(III).
-
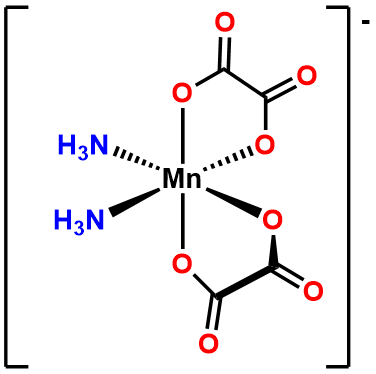
- Answer c. [CoCl4]2- .
-
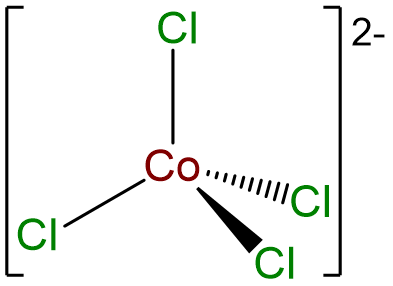
- Answer d. trans-diamminebis(ethylenediamine)Nickel(2+) tetracyanopalladate(2-).
-
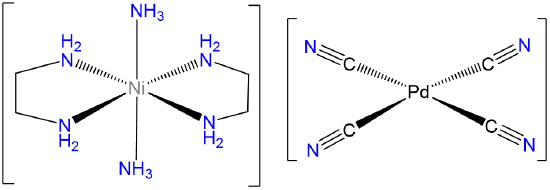
Note that since the Pd in [Pd(CN)4]2- is Pd2+ it will be square planar.
- Answer e. \(\Lambda\)-bis(ethylenediamine)cobalt(III)- μ-amido μ-hydroxo-\(\Delta\)-bis(ethylenediamine)cobalt(III).
-
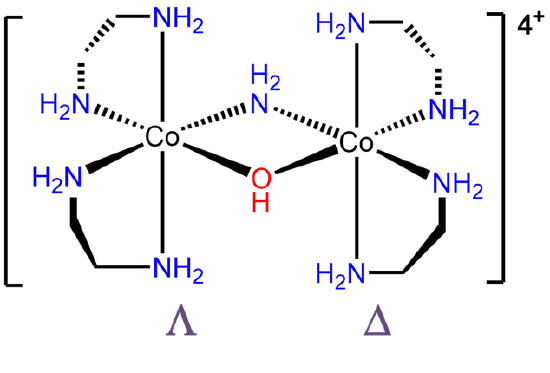 .
.
Draw all the stereoisomers of the following real and hypothetical complexes. You may assume that
- complexes in which the metal has a coordination number of six are octahedral
- complexes in which the metal has a coordination number of five are trigonal bipyramidal
- complexes in which PtII , PdII , or RhI, or IrI have a coordination number of four are square planar
- other complexes in which the metal has a coordination number of four will be tetrahedral
- [IrCl(CO)(PPh3)2]
- [CoCl3(NH3)3]
- [CoCl2(H2O)2(NH3)2]+
- [CoBrCl(H2O)2(NH3)2]+
- [CoBrClI(NH3)3]
- Answer a. [IrCl(CO)(PPh3)2]
-
This is a 4-coordinate IrI complex and, as such will be square planar. Since two of the ligands are identical, it will have cis and trans isomers. The trans isomer is famous for its ability to form adducts and is called Vaska's complex.
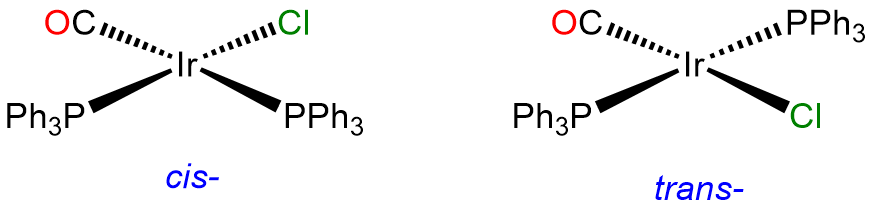
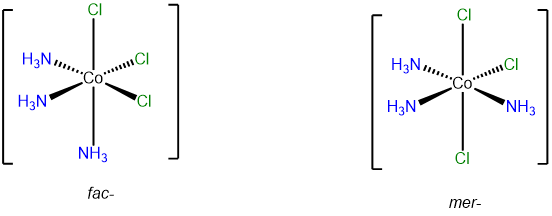
- Answer b. [CoCl3(NH3)3]
-
This complex contains three ammine and three chloro ligands and so will have fac and mer isomers.
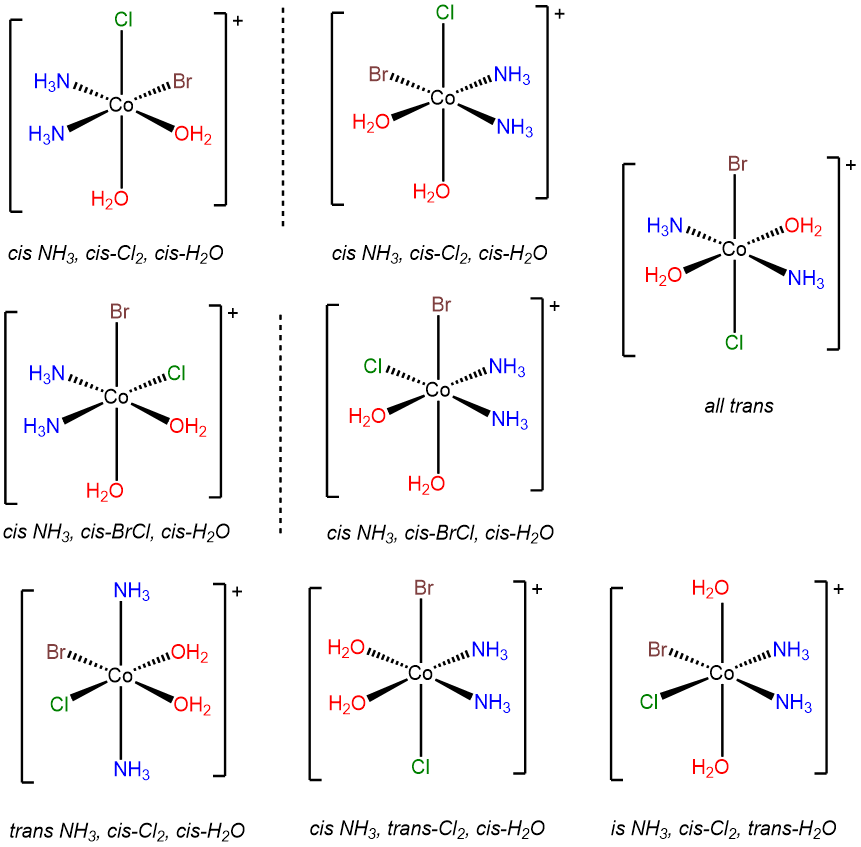
- Answer c. [CoCl2(H2O)2(NH3)2]+
-
This is a case of an MA2B2C2 system (A = Cl-, B = H2O, C = NH3) involving multiple cis and trans relationships. The six stereoisomers are shown below.
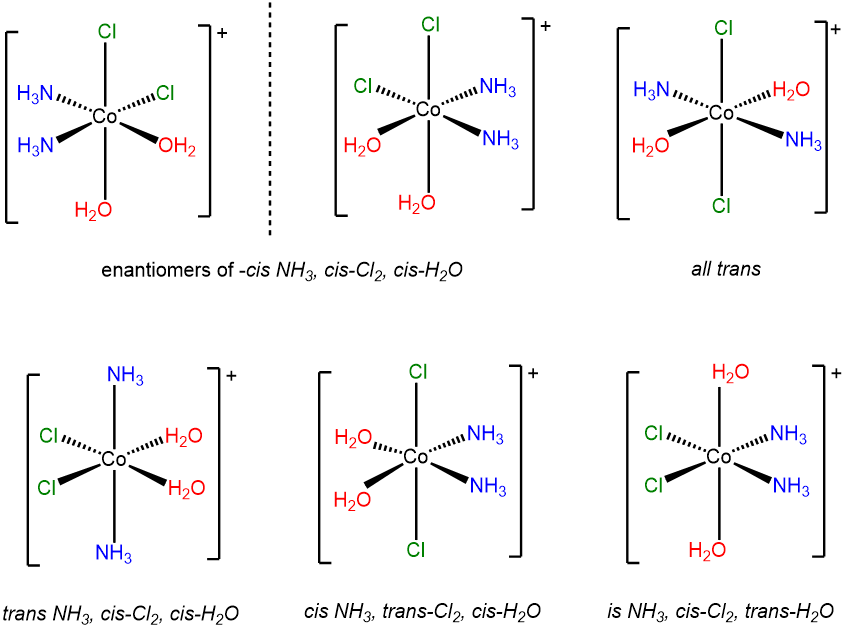
-
Since it may not be obvious how to arrive at a set of isomers like the ones above, it is worth considering how one might work through the possibilities for a system of ligands like this one. Several systems may be used to systematically identify isomers. Once approach is the Macbdef system described in Note \(\sf{\PageIndex{1}}\) at the end of these exercises. The solutions presented here and in subsequent problems employ a variant of that approach.
- Start by fixing one set of ligands. In this case the chloro ligands were first fixed as cis to one another. Then the remaining ligands might be cis or trans to one another, although since the chloro ligands are already cis, the ammine and aqua ligands cannot both be trans at the same time. Thus for cis chloro ligands the possibilities for the others are:
- cis-H2O ,cis-NH3,
- cis--H2O, trans-NH3
- trans-H2O, cis-NH3
- Swap the configuration of the ligand set you started with. In this case it means placing the chloro ligands trans to one another. From that configuration, the possibilities for the ammine and aqua ligands are
- cis-H2O ,cis-NH3,
- trans-H2O, trans-NH3
- Check for enantiomers and create mirror images of any chiral complexes you drew. The easiest way to do this is to assign point groups. However, it turns out that the octahedral all-cis case is D3 and formally equivalent to the symmetry of a tris chelate, as shown below.
- finally, check to make sure you didn't include the same complex twice. Humans do make mistakes after all.
- Start by fixing one set of ligands. In this case the chloro ligands were first fixed as cis to one another. Then the remaining ligands might be cis or trans to one another, although since the chloro ligands are already cis, the ammine and aqua ligands cannot both be trans at the same time. Thus for cis chloro ligands the possibilities for the others are:
- Answer d. [CoBrCl(H2O)2(NH3)2]+
-
This problem is analogous to the one above except that this complex contains a bromo and chloro ligand in place of the two chloro ligands in [CoCl2(H2O)2(NH3)2]+. Consequently, when the bromo and chloro ligands are cis to one another, additional possibilities for isomers arise based on whether ammine or aqua ligands are trans to the chloro and bromo. The result is eight isomers.
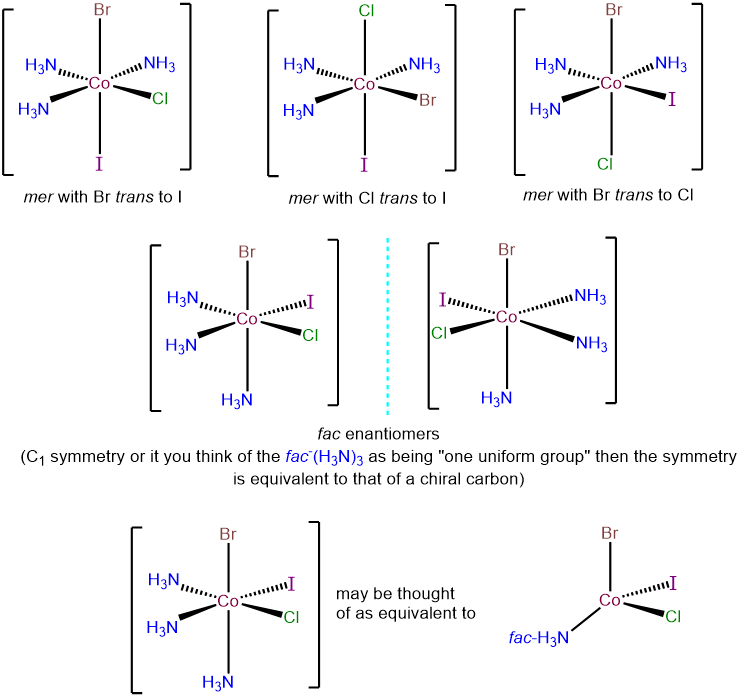
- Answer e. [CoBrClI(NH3)3]
-
There are two possibilities for this complex - a fac-(NH3)3 and a mer-(NH3)3 arrangement. These may be taken as starting points for examining the possible permutations for the Cl-, Br-, and I- ligands. The top row presents the three possibilities within the mer-(NH3)3 arrangement; each corresponds to a different ligand trans to an ammine ligand. The bottom row presents the two possible isomers with a fac-(NH3)3 arrangement. In each, the Cl-, Br-, and I- ligands are trans to ammine ligands. However, the complexes possess C1 symmetry and so are chiral and exist as enantiomers.
Ignoring ring twist, draw all the stereoisomers of the following real and hypothetical octahedral complexes.
- [CoBr2Cl2(en)]-
- [CoBrCl(en)2]+
- [CoBrCl(gly)2]-
- [Co(en)3]3+
- [Co(gly)3]
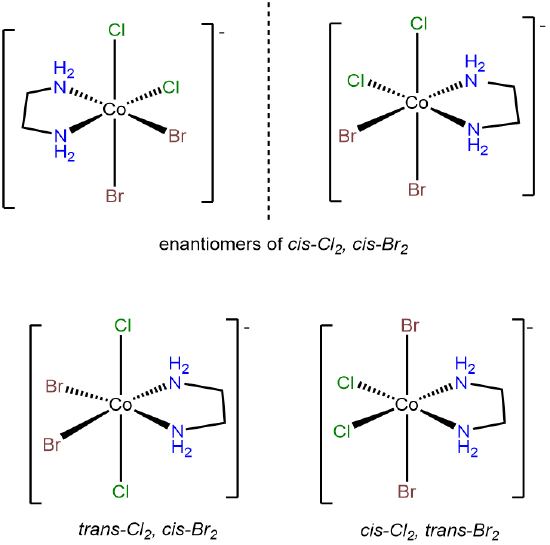
- Answer a. [CoBr2Cl2(en)]-
-
This complex is analogous to [CoCl2(H2O)2(NH3)2]+ in possessing pairs of identical ligating groups. The main difference is that in [CoBr2Cl2(en)]- the two amine ligating group of the en ligand are restricted to a cis arrangement. Under the MABCDEF system explained in Note \(\PageIndex{1}\), [CoCl2(H2O)2(NH3)2]+ may be MA2B2C2, but this complex, [CoBr2Cl2(en)]-, is M(AA)B2C2. The isomers are:
- Answer b. [CoBrCl(en)2]+
-
The key to problems like this is to focus on the unique ligands, in this case Br- and Cl-. These can exist in either a cis or trans arrangement. The trans form is achiral, but in the case where Br- and Cl- are cis, \(\Lambda\) and \(\Delta\) enantiomers are possible. The result is three isomers.
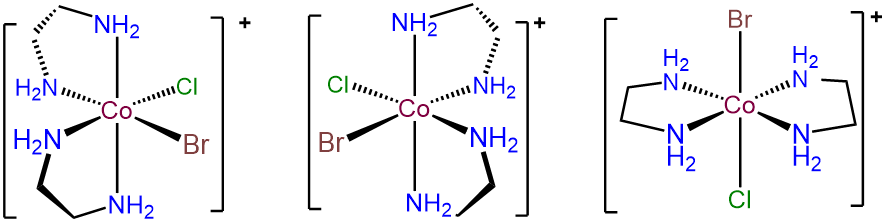
- Answer c. [CoBrCl(gly)2]-
-
This case is analogous to the one above, but this time the bidentate ligand, gly, possesses distinguishable binding sites. Thus there are additional permutations involving how the gly ligands are bound relative to one another and/or whether the O or N end of the gly is bound trans to Br or Cl. The result is 11 different isomers, which are given below.
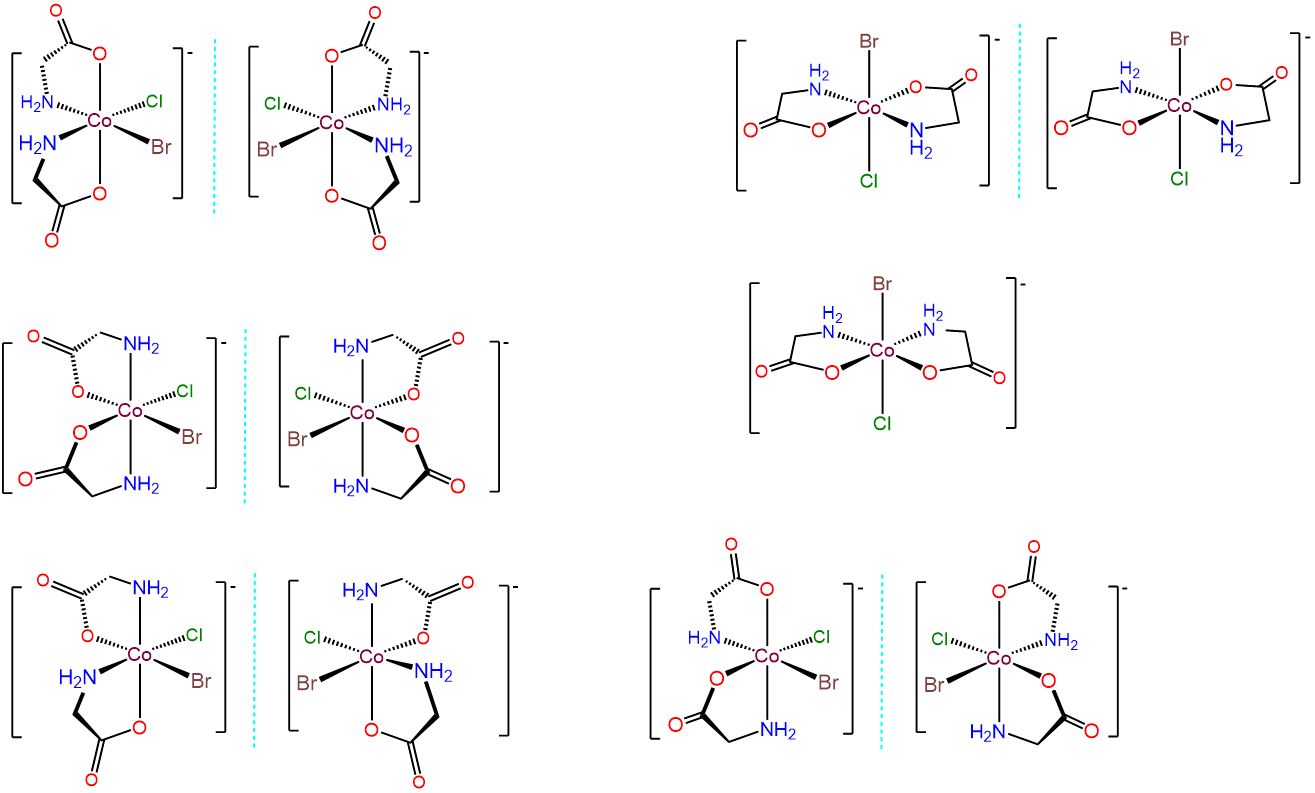
- Answer d. [Co(en)3]3+
-
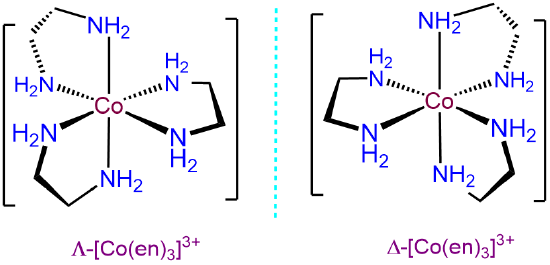
As a tris-chelate of symmetric bidentate ligands, ignoring ring twist, [Co(en)3]3+ will only exhibit \(\Lambda\) and \(\Delta\) isomerism.
- Answer e. [Co(gly)3]
-
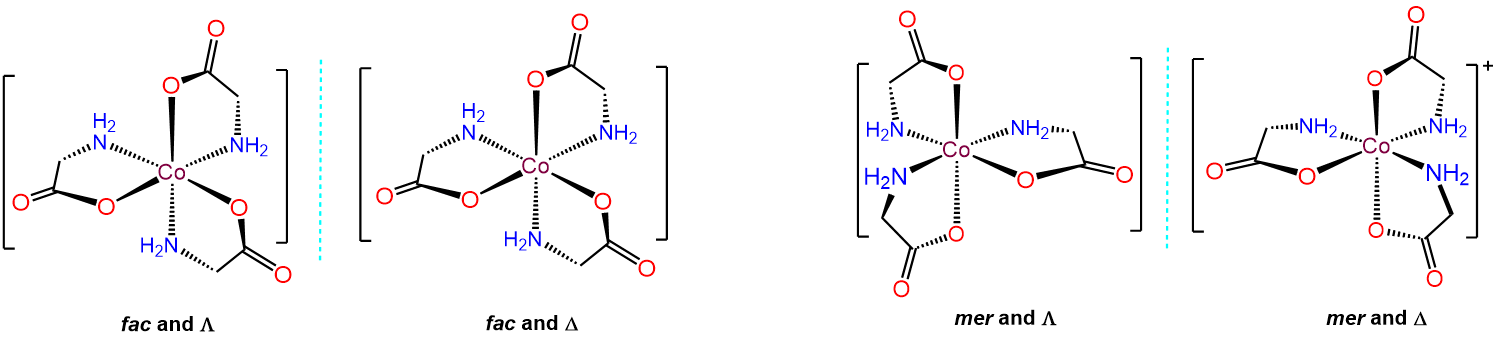
Since there are three gly ligands, each of which have carboxy and amine ends, the allowable arrangements involve whether the resulting three carboxy and three amine ends are oriented in a mer or fac arrangement. This gives two possibilities, each of which can exist as either the \(\Lambda\) or \(\Delta\) enantiomer, for a total of four isomers, which are given below.
Ignoring ring twist, draw all chemically reasonable stereoisomers for the following real and hypothetical complexes. You may assume that
- complexes in which the metal has a coordination number of six are octahedral
- complexes in which the metal has a coordination number of five are trigonal bipyramidal
- complexes in which PtII , PdII , or RhI, or IrI have a coordination number of four are square planar
- other complexes in which the metal has a coordination number of four will be tetrahedral
- [Pt(en)(SCN)2]
- [Pt(NH3)2(SCN)2]
- [Co(en)2(SCN)2]+
- Answer a. [Pt(en)(SCN)2]
-
The Pt in this neutral complex must be Pt2+ to balance the negative charges of the two SCN- ligands. Complexes of Pt2+ are square planar and four coordinate, consistent with the bidentate en and two thiocyanato ligands. Of the ligands, the en ligand must bind in a cis arrangement. Consequently, the two SCN- ligands will be in a cis arrangement as well. The isomers will therefore only differ in whether the two SCN- bind \(\kappa\)N or \(\kappa\)S. The possibilities are:
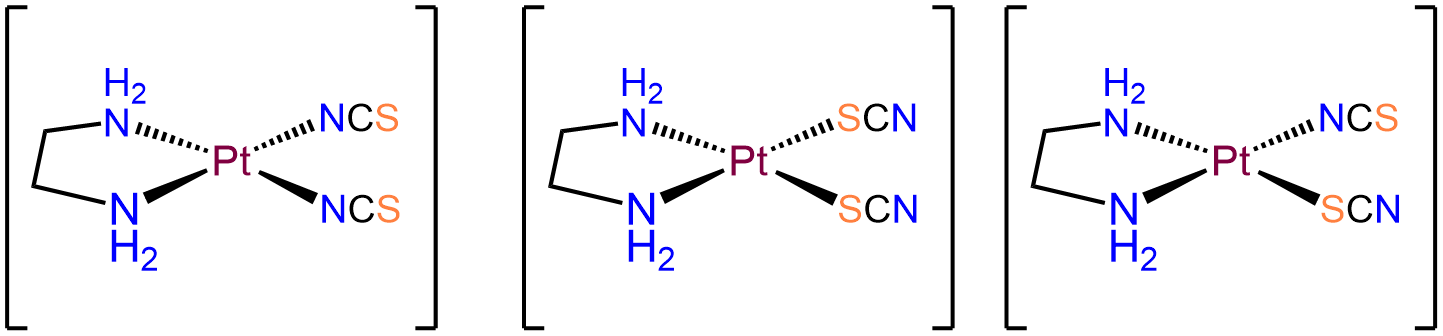
- Answer b. [Pt(NH3)2(SCN)2]
-
As with the preceding example, this will be a square planar Pt2+ complex. The main difference is that this time the coordinated nitrogens are not constrained to adopt a cis arrangement so there will be both cis and trans isomers.
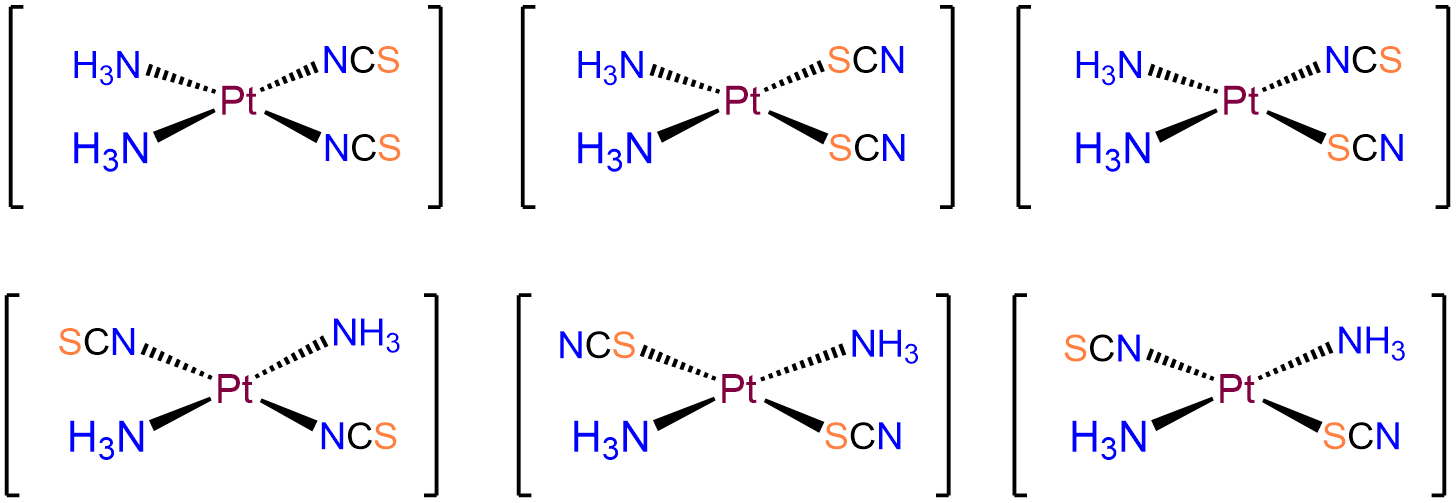
- Answer c. [Co(en)2(SCN)2]+
-
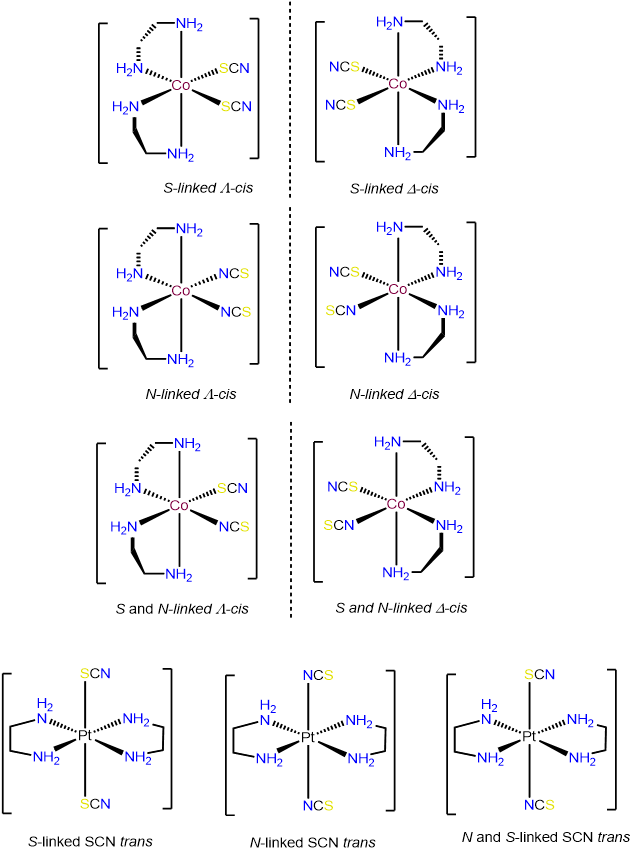
Ignoring ring twist, draw all chemically reasonable stereoisomers for the following real and hypothetical complexes. You may assume that
- complexes in which the metal has a coordination number of six are octahedral
- complexes in which the metal has a coordination number of five are trigonal bipyramidal
- complexes in which PtII , PdII , or RhI, or IrI have a coordination number of four are square planar
- other complexes in which the metal has a coordination number of four will be tetrahedral
- [Ru(bpy)(phen)(dppe)]2+
- [CoClF(PPh3)(py)]-
- [Ni(en)2(NO2)2]
- [Fe(H2O)3(SCN)3]
- [PtClF(PPh3)(py)]
- [CoBr2Cl(NH3)3]
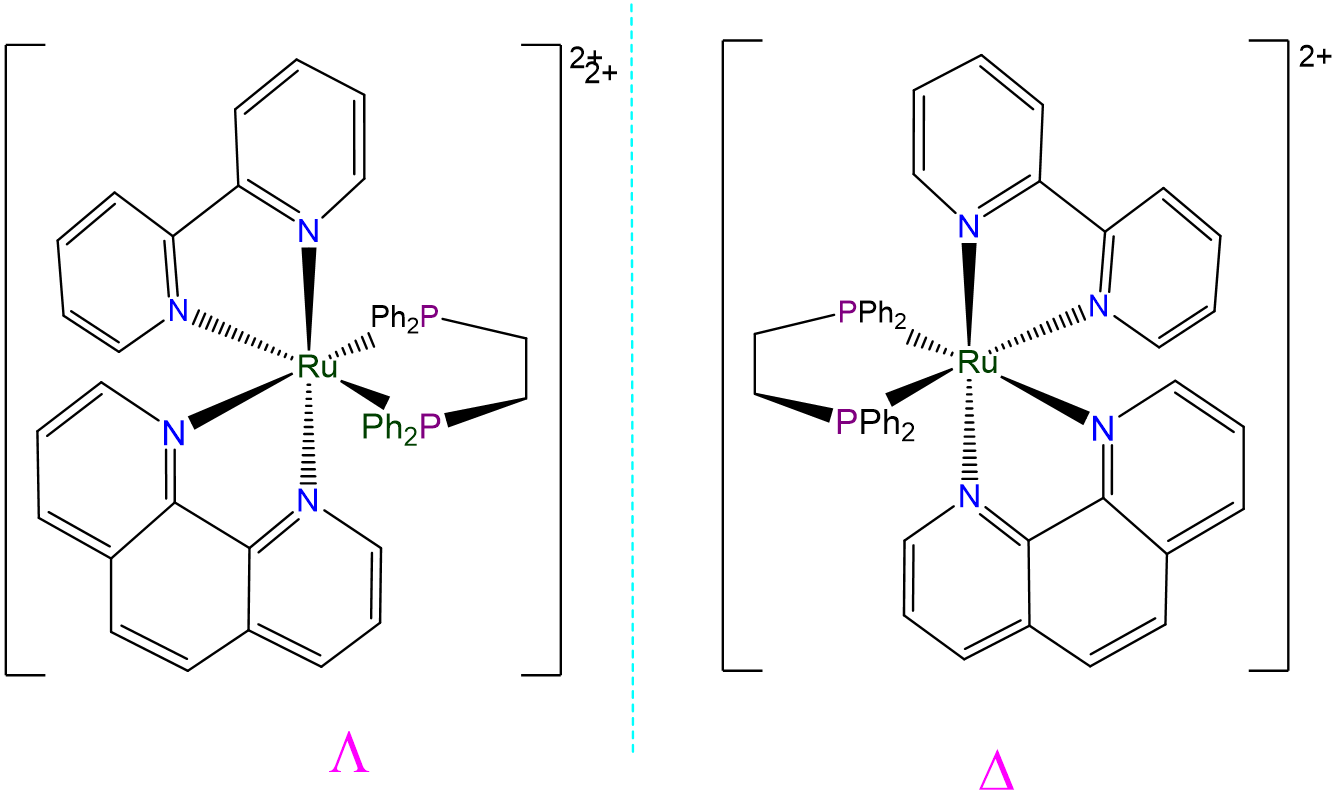
- Answer a. [Ru(bpy)(phen)(dppe)]2+
-
This complex is an octahedral tris-chelate containing symmetric ligands. As such it will exhibit \(\Lambda\) and \(\Delta\) isomers:
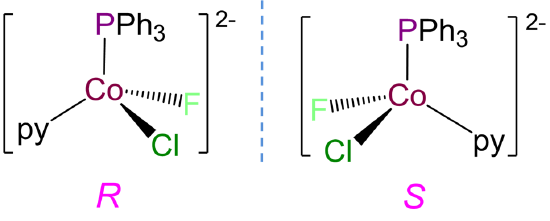
- Answer b. [CoClF(PPh3)(py)]-
-
This complex has a coordination number of 4 and contains a Co2+ ion with a d7 electron configuration, so a tetrahedral geometry is expected. Tetrahedral complexes like this one with four different ligands are chiral and can form R and S enantiomers.
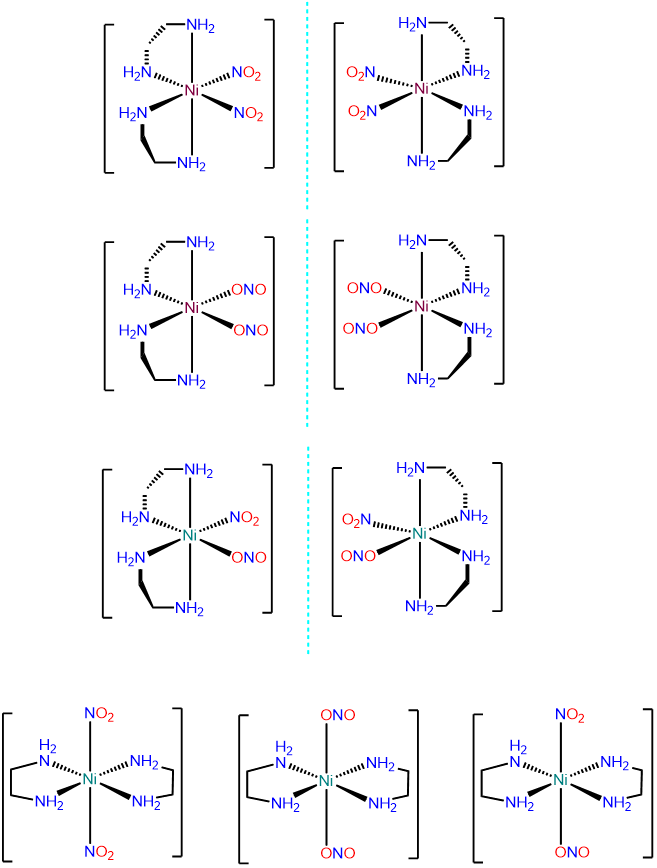
- Answer c. [Ni(en)2(NO2)2]
-
This is an octahedral bis-chelate and will exist in \(\Lambda\) and \(\Delta\) configurations. Within each configuration the NO2- ligands can exist as \(\kappa\)N and \(\kappa\)O, leading to the following possibilities:
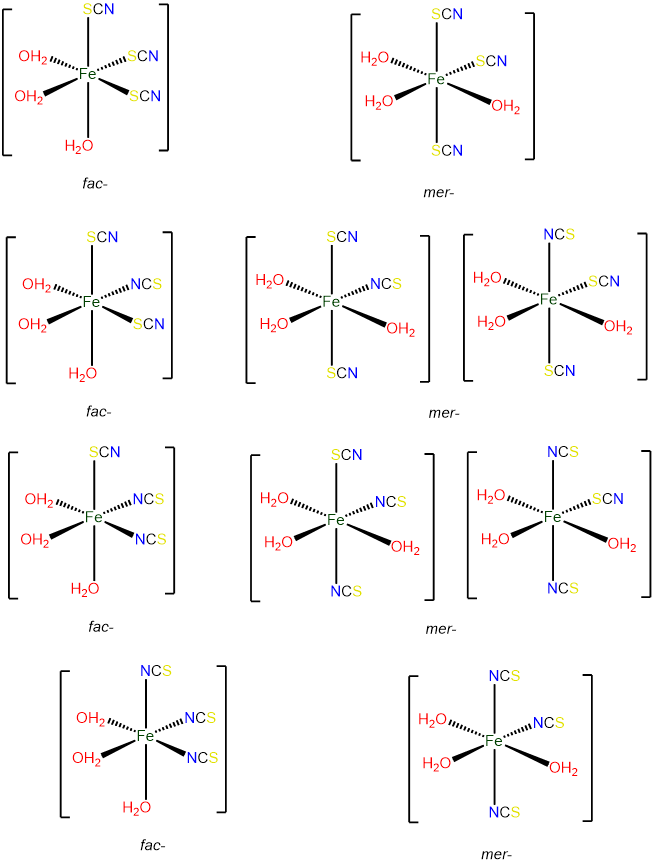
- Answer d. [Fe(H2O)3(SCN)3]
-
As an octahedral complex with three identical ligands it can exist in mer and fac configurations, with the ambidentate SCN ligand providing additional possibilities for isomerism.
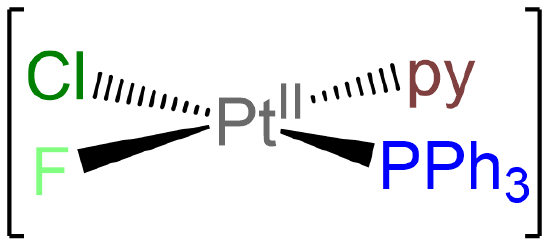
- Answer e. [PtClF(PPh3)(py)]
-
As a square planar complex with four nonidentical ligands, this complex exists as a single isomer.
- Answer f. [CoBr2Cl(NH3)3]
-
As an octahedral complex with three identical ligands it will exhibit mer and fac isomerism. In addition, it will have two mer configurations that differ in terms of the cis and trans relationships between the bromo and chloro ligands.
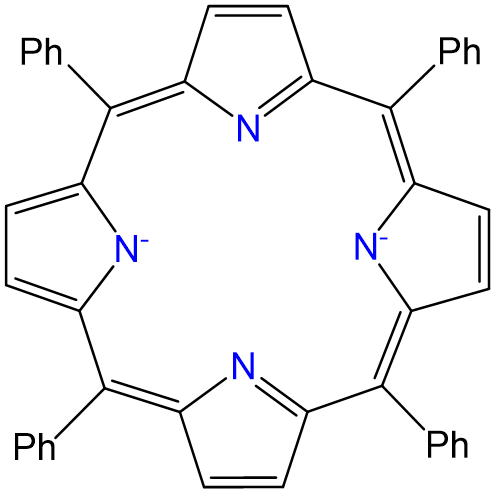
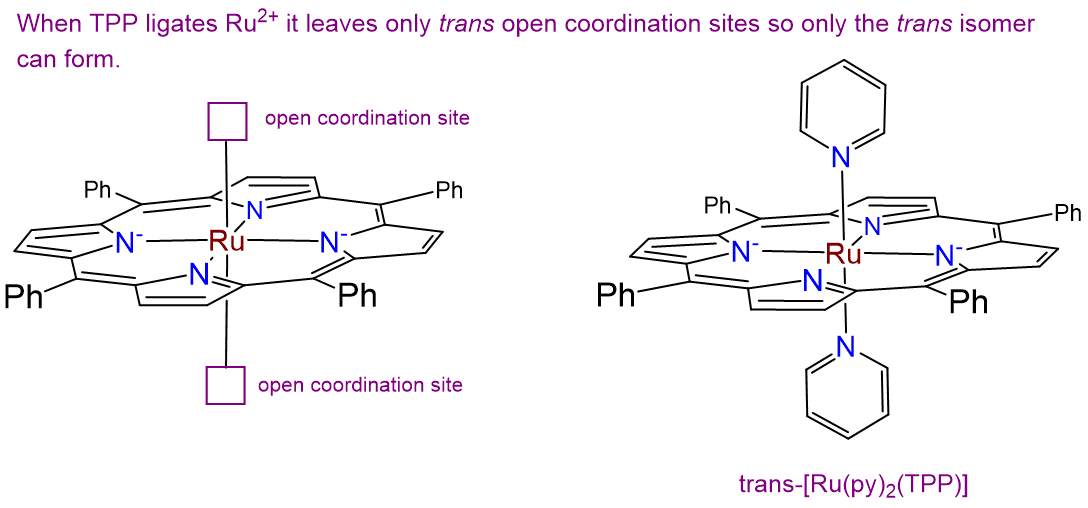
Complexes of formula Ru(TPP)py2 have been prepared, in which TPP is tetraphenylporphyrin, which binds metals in the form given below. Draw all isomers of Ru(TPP)py2.
- Answer
-
There is only one isomer. While normally complexes containing two identical ligands (in this case py) can exhibit cis and trans isomerism, in this case the planar tetraphenylporphyrin ring ligates the Ru2+ ion in a square planar arrangement, as shown at left in the image below. This leaves only a pair of trans coordination sites for the chloro ligands to occupy, giving the isomer shown at right below.
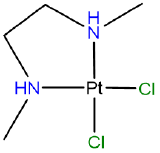
Draw the diastereomers formed due to the chirality of the amine nitrogen atoms in [PtCl2(N,N'-dimethylethane-1,2-diamine)] which has the atomic connectivity represented below
- Answer
-
The diastereomers will differ in whether the N atoms adopt an R or S configuration at the nitrogen atoms. The possible permutations are (R,R), (S,S), (R,S), and (S,R). However, as may be seen from the image below, the (R,S) and (S,R) configurations are identical (the two projections shown can be interconverted through a C2 rotation along an axis bisecting the Cl-Pt-Cl unit). As a result there are only three unique isomers. Of these, the (R,R) and (S,S) configurations are enantiomers (they are mirror images by reflection in the PtCl2N2 plane). Note that in solving problems like this one it can be helpful to keep track of possible isomers by assigning the stereochemistry at each chiral center as R or S using the Cahn-Ingold-Prelog-convention, though it is not strictly necessary to do so.
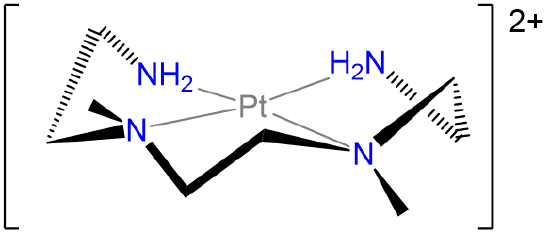
Label the conformations of all chelate rings in the structure below.
- Answer
-
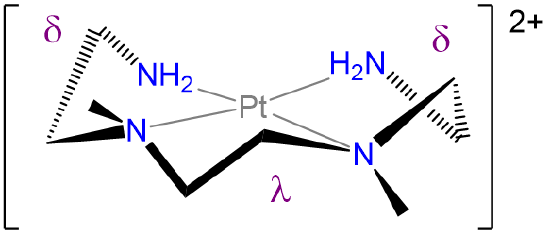 .
.
Appendix: The MABCDEF bookkeeping system for identifying isomers
The Mabcdef or MABCDEF system is one method for identifying the number of isomers in an octahedral complex, although since it is really just a bookkeeping and organizational system it can easily be extended to other geometries as well. The M in Mabcdef stands for metal and the other letters are used to stand in for ligands. The basic approach involves
- classifying the ligands as A, B, C, D, E, or F in order of multiplicity. Thus for
[Cr(NH3)6]3+ A = NH3; there are no B, C, D,E, or F ligands; and the complex is classified as MA6
[CoCl(NH3)5]2+ A = NH3, B = Cl-, and the complex is MA5B
[CrCl2(H2O)2(NH3)2]+ A = Cl-, B = H2O, C = NH3, and the complex is MA2B2C2
- in the classification above, multidentate ligands are typically classified before monodentate ones and are designated AA, AB, ABC, ABA, etc. based on the symmetry of the attachment points. Thus
en has identical attachment amine points and is AA
gly has a carboxy and amine attachment points and is AB
trien is ABA
CoCl2(en)2+ is M(AA)2B2
CoCl2(gly)2- is M(AB)2C2
CoCl2(en)(gly) is M(AA)(AB)C2
- Systematically list out the possible trans arrangements of ligands by
- assigning one pair of ligands to be trans to one another.
- Then systematically list out the other possible trans pairs by permuting the remaining trans arrangements. It can help to organize the permutations in a table, such as that shown below for an MABCDEF complex where A and B are assigned trans. In looking at the table notice how the second set of trans permutations is systematically varied. This helps ensure that no possibility is skipped.
- Go through the list of isomers and remove any duplicates you generated so far. For instance, notice in the table below that the last three stereoisomers are identical with the first three (e.g., stereoisomer 4 is identical to stereoisomer 3, 5 with 2, and 6 with 1).
| Stereoisomer 1 | Stereoisomer 2 | Stereoisomer 3 |
Stereoisomer 4 (same as isomer 3) |
Stereoisomer 5 (same as isomer 2) |
Stereoisomer 6 (same as isomer 1) |
| trans AB (fixed) | trans AB (fixed) | trans AB (fixed) | trans AB (fixed) | trans AB (fixed) | trans AB (fixed) |
| trans CD | trans CE | trans CF | trans DE | trans DF | trans EF |
| trans EF | trans DF | trans DE | trans CF | trans CE | trans CD |
- If the complex possesses multidentate ligands that demand that certain groups exist and cis pairs, then also remove any configurations which do not agree with the known binding capability of the ligand (e.g., the two amine groups of ethylenediamine cannot be trans to one another, so if you have an en ligand, remove configurations like that from the list).
- Next, swap or permute the original trans pair and repeat the process you just followed. In the case of Mabcdef this gives the following results:
| Isomer | "fixed" trans pair | Additional trans pairs | |
| 1 | AB | CD | EF |
| 2 | AB | CE | DF |
| 3 | AB | CF | DE |
| 4 | AC | BD | EF |
| 5 | AC | BE | BF |
| 6 | AC | BF | DE |
| 7 | AD | BC | EF |
| 8 | AD | BE | CF |
| 9 | AD | BF | CE |
| 10 | AE | BC | DF |
| 11 | AE | BD | CF |
| 12 | AE | BF | CD |
| 13 | AF | BC | DE |
| 14 | AF | BD | CE |
| 15 | AF | BE | CD |
- Since the procedure explained above only identifies isomers based on unique trans pairings, it does not identify when a configuration is chiral and corresponds to a pair of enantiomers. Any enantiomers can be identified by drawing out the complexes and either classifying their point groups or by drawing their mirror images and checking if they are superimposable. In the MABCDEF case - i.e., where all the ligands are different - all of the isomers identified have C1 symmetry so are chiral. This means there will be a pair of enantiomers for each, giving 15 x 2 = 30 different stereoisomers.
References
1. These examples are taken from http://wwwchem.uwimona.edu.jm/courses/inorgnom.html
2. Contakes S. M.; Rauchfuss, T.B. Chem. Commun. 2001, 553-554.
3. Shriver, D. F.; Shriver, S. A.; Anderson, S. E., Inorg. Chem. 1965, 4(5), 725-730.
4. Zelewsky, A. v., Stereochemistry of Coordination Compounds Wiley, 1996.
5. In the past it was difficult to determine absolute configurations from X-ray data alone, but recent advances have made it easier to do so.
6. Pavan M. V. Raja & Andrew R. Barron "Circular Dichroism Spectroscopy and its Application for Determination of Secondary Structure of Optically Active Species" in Physical Methods in Chemistry and Nano Science https://chem.libretexts.org/Bookshelves/Analytical_Chemistry/Book%3A_Physical_Methods_in_Chemistry_and_Nano_Science_(Barron)/07%3A_Molecular_and_Solid_State_Structure/7.07%3A_Circular_Dichroism_Spectroscopy_and_its_Application_for_Determination_of_Secondary_Structure_of_Optically_Active_Species
7. Berova, N.; Bari, L. D.; Pescitelli, G., Chemical Society Reviews 2007, 36 (6), 914-931.
8. Of course, if one set of ligands occupies a meridional plane, then the other three ligands will be oriented in an equatorial one. The reason they may both be considered meridional is because if the complex were rotated, the equatorial plane would be meridional and vice versa. From that point of view both might be considered meridional planes - albeit not at the same time.
9. Bite angles are taken from Mansell, S. M., Catalytic applications of small bite-angle diphosphorus ligands with single-atom linkers. Dalton Transactions 2017, 46 (44), 15157-15174.
10. Hancock, R. D., The pyridyl group in ligand design for selective metal ion complexation and sensing. Chemical Society Reviews 2013, 42 (4), 1500-1524.
11. Sasi, D.; Ramkumar, V.; Murthy, N. N., Bite-Angle-Regulated Coordination Geometries: Tetrahedral and Trigonal Bipyramidal in Ni(II) with Biphenyl-Appended (2-Pyridyl)alkylamine N,N'-Bidentate Ligands. ACS Omega 2017, 2 (6), 2474-2481.
12. Ehnbom, A.; Ghosh, S. K.; Lewis, K. G.; Gladysz, J. A., Octahedral Werner complexes with substituted ethylenediamine ligands: a stereochemical primer for a historic series of compounds now emerging as a modern family of catalysts. Chemical Society Reviews 2016, 45 (24), 6799-6811.


