8.1.1.2: There are qualitative differences between the chemistry of the elements in the first two rows and those in the rest of the periodic table
- Page ID
- 199670
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The bonding characteristics of the elements do not vary gradually down the groups in the main group of the periodic table. Instead, there are significant discontinuities on moving between the first and second row elements and the second row elements and the rest of the periodic table. These differences are outlined below and depicted schematically in Figure \(\PageIndex{1}\).
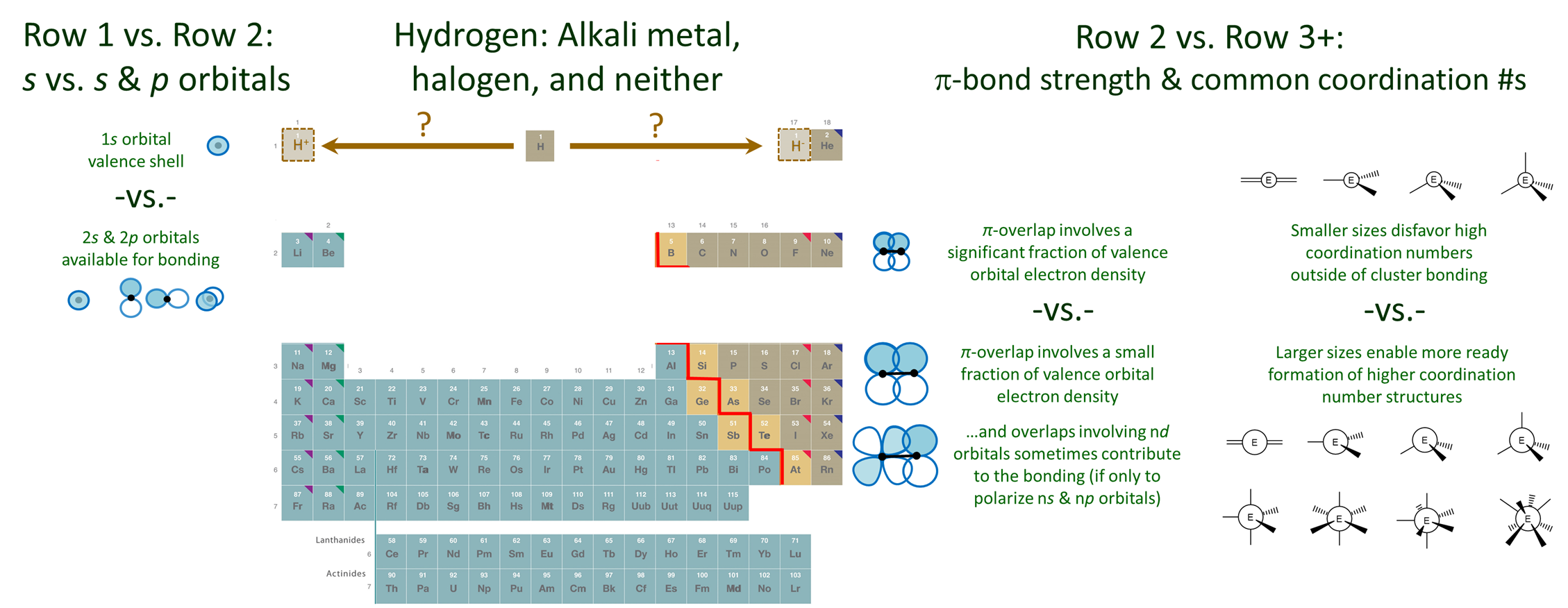
The first row elements have a unique chemistry because their valence shell is only a 1s orbital.
In the case of He the 1s orbital is full, compact, and of low energy. Consequently He is extremely inert, to the point where no compounds of He are known.
Hydrogen's 1s orbital is comparatively higher in energy. As a result H is more reactive. It tends to lose or gain its single electron but can also contribute to multicenter bonding.
Because of its chemical versatility the location of H in the periodic table is ambiguous. Even though its electronegativity is much greater than that of lithium, it is usually placed at the head of the alkali metals. This placement is consistent with its possession of a singe valence electron and the consequent readiness with which it loses an electron, particularly in aqueous media. However, hydrogen is also just short a single electron and so in other contexts it readily forms hydrides. Thus it might be placed at the head of the halogens. Although it is rare to place H above the halogens, in some tables H is placed above the table to emphasize this chemical versatility.
According to the uniqueness principle the second row elements are unique in their ability to form strong multiple bonds and their resistance to serving as high coordination number centers.
There are three reasons why the second row elements differ significantly from their heavier cogeners.
1. Only the second row elements form strong \(\pi\)-bonds. As depicted schematically in Figure \(\PageIndex{1}\), the second row elements are able to form strong \(\pi\) bonds since the fraction of electron density involved in the \(\pi\)-overlap is significant for the more compact orbitals and shorter bonds of the row 2 elements. In contrast, for row 3 and heavier elements, relatively little of the large and diffuse orbitals contributes to the overlap that stabilizes the \(\pi\)-bond. In consequence, \(\pi\)-bonds involving these elements are very weak and such bonds are relatively rare. This is because it is almost always more favorable for such elements to form multiple single bonds or engage in cluster bonding.
The tendency of Row 2 nonmetals to form strong \(\pi\) bonds in cases where their heavier cogeners form extended structures is apparent from the common allotropes formed by the p-block nonmetals. As shown in Figure \(\PageIndex{2}\), Row 3+ elements have a greater tendency to form extended structures held together by single bonds than their Row 2 counterparts.
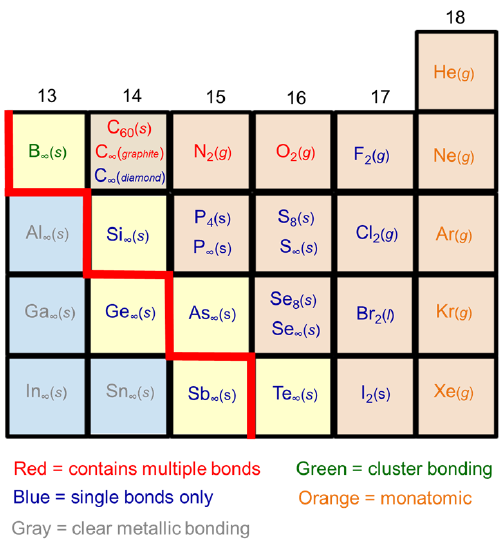
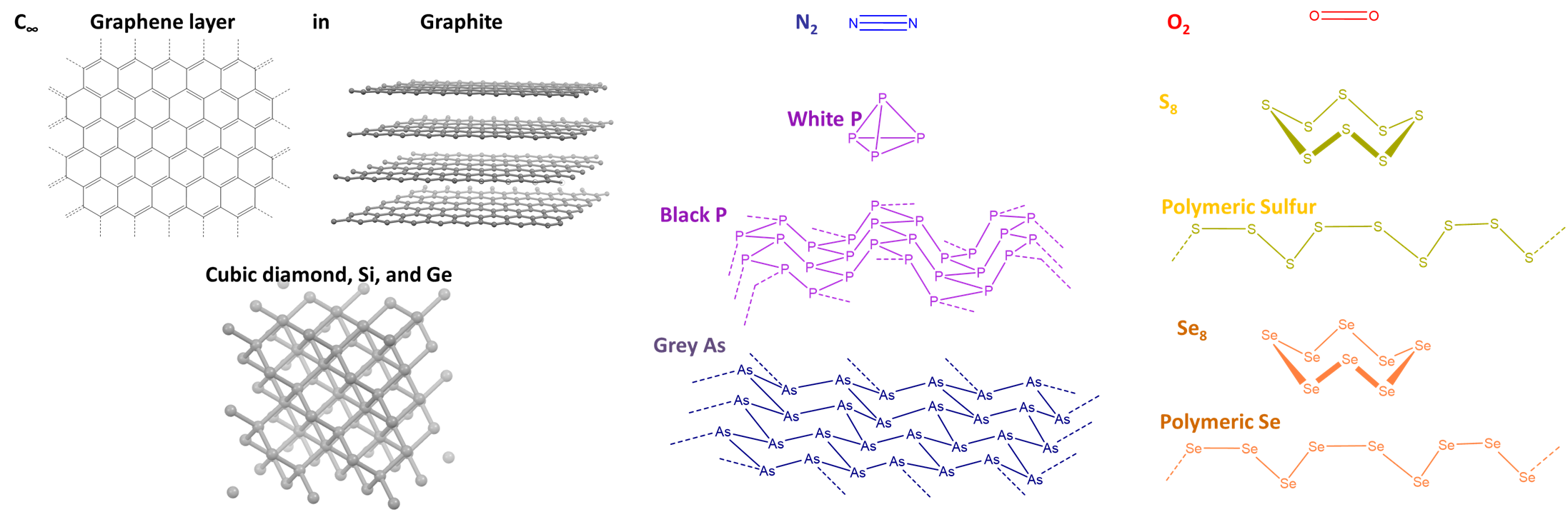
As shown in Figure \(\PageIndex{3}\), the Row 2 element carbon forms sheetlike structures involving multiple bonding (graphite, fullerenes, nanotubes) as well as 3D networks held together by single bonds (the diamond structure), while its heavier cogeners Si and Ge only form 3D networks. Similarly, nitrogen and oxygen form diatomic gases held together by multiple bonds, while their heavier cogeners form clusters (P), layers (As, Sb), or chains (S, Se, Te) held together by single covalent bonds.
2. The valence shell of the second row elements lacks low-lying nd orbitals. As a result, only the 2s and 2p type orbitals of second row elements significantly contribute to the bonding in their compounds. In contrast, the main group elements of row 3 and higher possess low lying unoccupied nd orbitals, which enable them to act as a \(\pi\) acid towards a ligand atom by forming \(d_{\pi}-p_{\pi}\) and \(d_{\pi}-d_{\pi}\) overlaps.
3. As depicted in Figure \(\PageIndex{1}\), when second row elements serve as a central atom, they do not readily exhibit coordination numbers higher than four. In contrast, the larger size of row 3 and heavier elements reduces the steric strain associated with the addition of multiple ligands about an element center. This makes it easier for these elements to form trigonal bipyramidal, octahedral, and other high coordination number structures.
Contributors and Attributions
Stephen M. Contakes, Westmont College


