8.1.1: The Periodic Table is an Organizing Concept in Main Group Chemistry
- Page ID
- 199659
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The chemical and physical properties of the main group compounds result from the electronic properties of their constituent atoms and ions. These atomic electronic properties are determined by the number of electrons present and the ground state orbitals they occupy. Of these electrons the chemically most important are the valence electrons and the orbitals they occupy, called valence orbitals. These valence electron counts and orbital occupancies vary systematically in a way that is reflected in the organization of the periodic table. Specifically, the number of valence electrons and the types of atomic orbitals they occupy are determined by the element’s group. This is reflected in the familiar block structure of the periodic table shown in Figure \(\PageIndex{1}\).
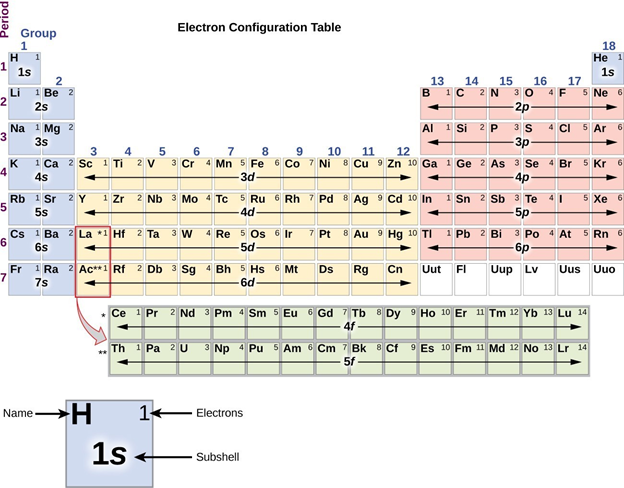
From Figure \(\PageIndex{1}\) it can be seen that the main group elements are those with nsx and ns2 npy type valence electron configurations – called s and p block elements. The exact occupancy of the s and p subshells increases with the total number of valence electrons from left to right across the periodic table as shown in Figure \(\PageIndex{2}\).

From Figure \(\PageIndex{2}\) it can be seen that elements within a group of the periodic table have the same configuration of s and p valence electrons. This is one reason why elements within the same group tend to have similar chemical properties.[1] Consequently, it is usually convenient to think and talk about the elements and their properties by group.
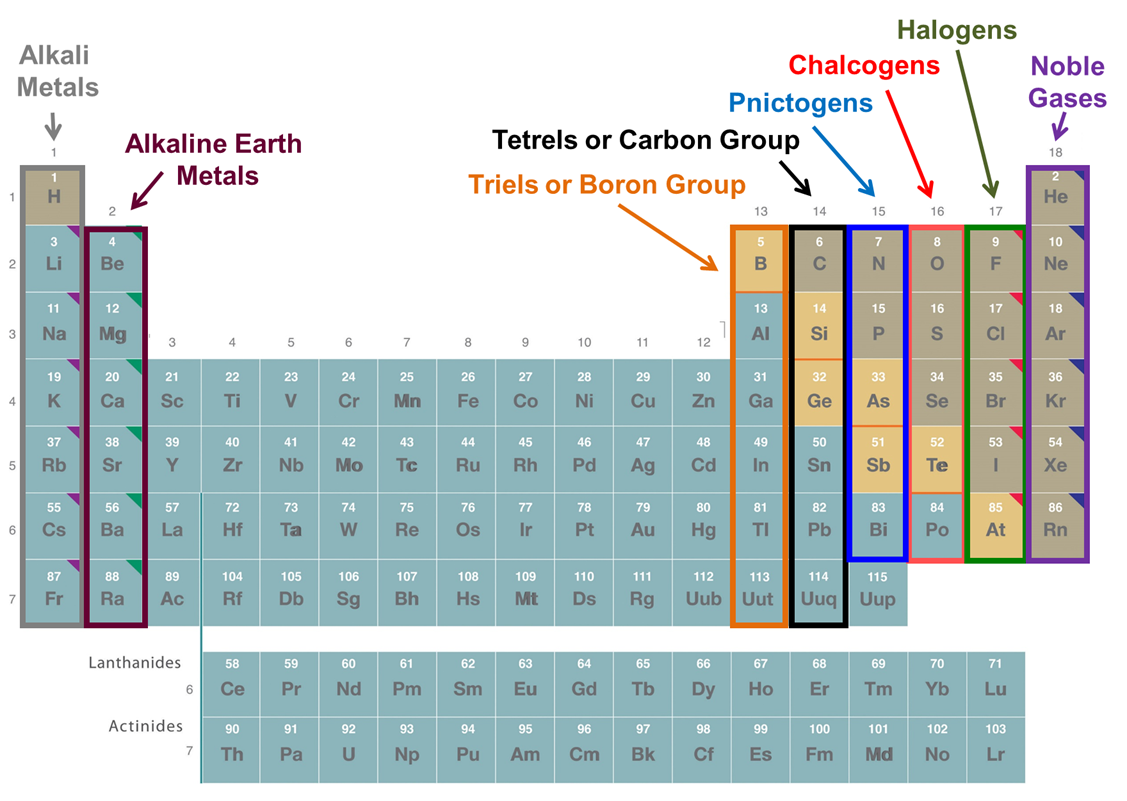
Groups may always be referred to by their group number or their first element. In addition, a number have common names that are widely used. These are given in Figure \(\PageIndex{3}\).
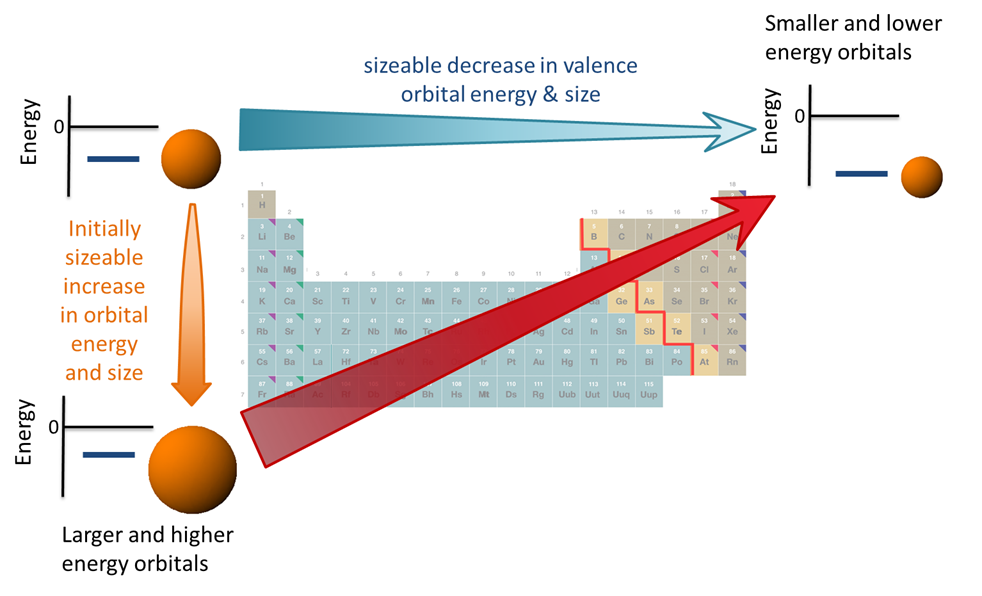
Further insight into the properties of the elements may be gained by considering how the systematic variation in electron configuration that occurs across the periodic table's rows interacts with the systematic variations in atomic properties that occur across rows and down groups. A detailed understanding of these properties, how they vary throughout the periodic table, and why they vary in the way they do will be developed in later sections. For now, it is only necessary to know the trends in valence orbital properties, which are:
- The valence orbital size tends to increase down a group as the principle atomic number increases. This increase in orbital size corresponds to lengthening of the average electron-nuclear distance and consequently a weakening of the valence electron-nucleus attraction.
- The valence orbital energy roughly decreases across a row as the effective nuclear charge, Z*, increases. The major factor driving this decrease in energy is the increase in electron-nucleus attraction as Z* increases.
- The valence orbital size roughly decreases across a row as the effective nuclear charge, Z*, increases. This decrease in size corresponds to a shortening of the valence electron-nuclear distance and strengthening of the valence electron-nucleus attraction. This size effect reinforces the aforementioned lowering of valence orbital energies, effective nuclear charge, although in general the lowering of energy due to decreasing size is less important than the lowering of energy due to increasing charge. That is because size decreases gradually from left to right while the effective nuclear charge increases by about 2/3 of a charge unit when moving from group to group.
These trends are summarized in Figure \(\PageIndex{4}\).
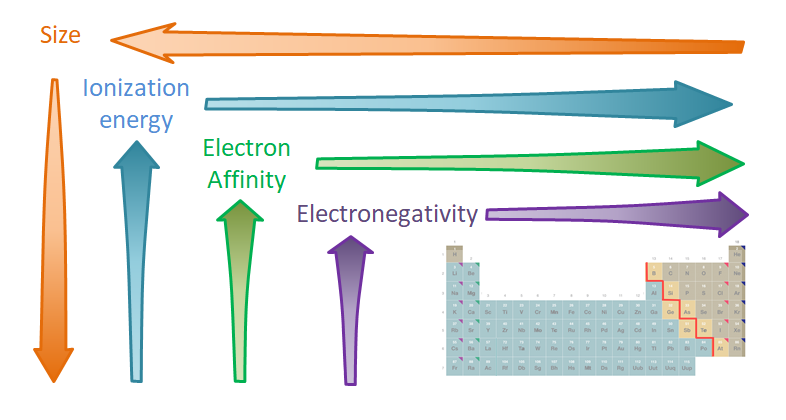
These valence orbital property trends affect two different classes of atomic properties. The first class includes the valence orbital size-related properties such as atomic radii and the \( \pi \)-bonding interaction strength. The second class contains electron-nucleus attraction-related properties comprising ionization energy, electron affinity, and electronegativity.
The consequences of the valence orbital property trends for atomic properties are as follows
- Atomic size increases down a group as the valence orbital becomes larger (n increases) and roughly decreases across a row as the effective nuclear charge increases.
- Ionization energy decreases down a group as the valence orbital becomes larger and roughly increases across a row as the effective nuclear charge increases.
- Electron affinity decreases down a group as the valence atomic orbital becomes larger and roughly increases across a row as the effective nuclear charge increases.
- Electronegativity decreases down a group as the lowest incompletely occupied atomic orbital becomes larger and roughly increases across a row as the effective nuclear charge increases.
These consequences are summarized in Figure \(\PageIndex{5}\).
These variations in turn explain the trends in main group element properties that are explored in the remainder of this chapter.
[1] Another is that the valence orbital energies tend to vary relatively little down a group, especially as one moves from row three downward.
Contributors and Attributions
Stephen M. Contakes (Westmont College)

