Ionic solids tend to be very stable compounds. The enthalpies of formation of the ionic molecules cannot alone account for this stability. These compounds have an additional stability due to the lattice energy of the solid structure. However, lattice energy cannot be directly measured. The Born-Haber cycle allows us to understand and determine the lattice energies of ionic solids.
Introduction
This module will introduce the idea of lattice energy, as well as one process that allows us to calculate it: the Born-Haber Cycle. In order to use the Born-Haber Cycle, there are several concepts that we must understand first.
Lattice Energy
Lattice Energy is a type of potential energy that may be defined in two ways. In one definition, the lattice energy is the energy required to break apart an ionic solid and convert its component atoms into gaseous ions. This definition causes the value for the lattice energy to always be positive, since this will always be an endothermic reaction. The other definition says that lattice energy is the reverse process, meaning it is the energy released when gaseous ions bind to form an ionic solid. As implied in the definition, this process will always be exothermic, and thus the value for lattice energy will be negative. Its values are usually expressed with the units kJ/mol.
Lattice Energy is used to explain the stability of ionic solids. Some might expect such an ordered structure to be less stable because the entropy of the system would be low. However, the crystalline structure allows each ion to interact with multiple oppositely charge ions, which causes a highly favorable change in the enthalpy of the system. A lot of energy is released as the oppositely charged ions interact. It is this that causes ionic solids to have such high melting and boiling points. Some require such high temperatures that they decompose before they can reach a melting and/or boiling point.
Born-Haber Cycle
There are several important concept to understand before the Born-Haber Cycle can be applied to determine the lattice energy of an ionic solid; ionization energy, electron affinity, dissociation energy, sublimation energy, heat of formation, and Hess's Law.
- Ionization Energy is the energy required to remove an electron from a neutral atom or an ion. This process always requires an input of energy, and thus will always have a positive value. In general, ionization energy increases across the periodic table from left to right, and decreases from top to bottom. There are some excepts, usually due to the stability of half-filled and completely filled orbitals.
- Electron Affinity is the energy released when an electron is added to a neutral atom or an ion. Usually, energy released would have a negative value, but due to the definition of electron affinity, it is written as a positive value in most tables. Therefore, when used in calculating the lattice energy, we must remember to subtract the electron affinity, not add it. In general, electron affinity increases from left to right across the periodic table and decreases from top to bottom.
- Dissociation energy is the energy required to break apart a compound. The dissociation of a compound is always an endothermic process, meaning it will always require an input of energy. Therefore, the change in energy is always positive. The magnitude of the dissociation energy depends on the electronegativity of the atoms involved.
- Sublimation energy is the energy required to cause a change of phase from solid to gas, bypassing the liquid phase. This is an input of energy, and thus has a positive value. It may also be referred to as the energy of atomization.
- The heat of formation is the change in energy when forming a compound from its elements. This may be positive or negative, depending on the atoms involved and how they interact.
- Hess's Law states that the overall change in energy of a process can be determined by breaking the process down into steps, then adding the changes in energy of each step. The Born-Haber Cycle is essentially Hess's Law applied to an ionic solid.
Using the Born-Haber Cycle
The values used in the Born-Haber Cycle are all predetermined changes in enthalpy for the processes described in the section above. Hess' Law allows us to add or subtract these values, which allows us to determine the lattice energy.
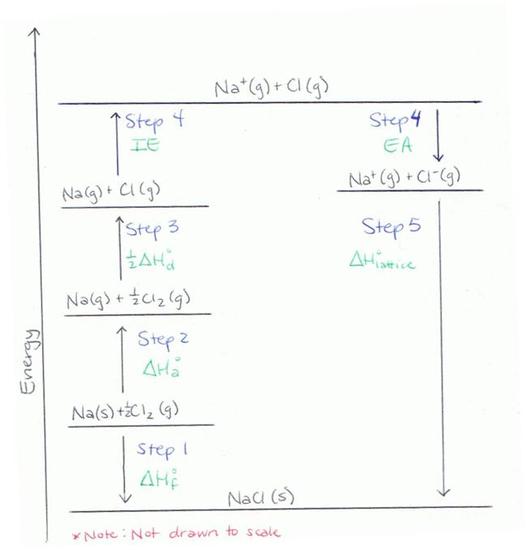
Step 1
Determine the energy of the metal and nonmetal in their elemental forms. (Elements in their natural state have an energy level of zero.) Subtract from this the heat of formation of the ionic solid that would be formed from combining these elements in the appropriate ration. This is the energy of the ionic solid, and will be used at the end of the process to determine the lattice energy.
Step 2
The Born-Haber Cycle requires that the elements involved in the reaction are in their gaseous forms. Add the changes in enthalpy to turn one of the elements into its gaseous state, and then do the same for the other element.
Step 3
Metals exist in nature as single atoms and thus no dissociation energy needs to be added for this element. However, many nonmetals will exist as polyatomic species. For example, Cl exists as Cl2 in its elemental state. The energy required to change Cl2 into 2Cl atoms must be added to the value obtained in Step 2.
Step 4
Both the metal and nonmetal now need to be changed into their ionic forms, as they would exist in the ionic solid. To do this, the ionization energy of the metal will be added to the value from Step 3. Next, the electron affinity of the nonmetal will be subtracted from the previous value. It is subtracted because it is a release of energy associated with the addition of an electron.
*This is a common error due to confusion caused by the definition of electron affinity, so be careful when doing this calculation.
Step 5
Now the metal and nonmetal will be combined to form the ionic solid. This will cause a release of energy, which is called the lattice energy. The value for the lattice energy is the difference between the value from Step 1 and the value from Step 4.
--------------------------------------------------------------------------------------------------------------------------------------------
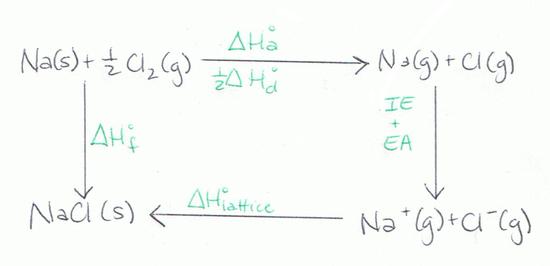
The diagram below is another representation of the Born-Haber Cycle.
Equation
The Born-Haber Cycle can be reduced to a single equation:
Heat of formation= Heat of atomization+ Dissociation energy+ (sum of Ionization energies)+ (sum of Electron affinities)+ Lattice energy
*Note: In this general equation, the electron affinity is added. However, when plugging in a value, determine whether energy is released (exothermic reaction) or absorbed (endothermic reaction) for each electron affinity. If energy is released, put a negative sign in front of the value; if energy is absorbed, the value should be positive.
Rearrangement to solve for lattice energy gives the equation:
Lattice energy= Heat of formation- Heat of atomization- Dissociation energy- (sum of Ionization energies)- (sum of Electron Affinities)
References
- Cheetham, A.K. and P. Day. Solid State Chemistry. Oxford: Clarendon Press, 1992.
- Jenkins, H. Donald B. "Thermodynamics of the Relationship between Lattice Energy and Lattice Enthalpy." Journal of Chemical Education. Vol. 82, P. 950-952. Coventry, West Midlands, UK: University of Warwick, 2005.
- Ladd, Mark. Crystal Structures: Lattices and Solids in Stereoview. Chichester: Horwood, 1999.
- Ladd, Mark. Chemical Bonding in Solids and Fluids. Chichester: Horwood, 1994.
- Suzuki, Takashi. Free energy and Self-interacting Particles. Boston: Birkhauser, 2005.
Problems
- Define lattice energy, ionization energy, and electron affinity.
- What is Hess' Law?
- Find the lattice energy of KF(s).
Note: Values can be found in standard tables.
- Find the lattice energy of MgCl2(s).
- Which one of the following has the greatest lattice energy?
- A) MgO
- B) NaC
- C) LiCl
- D) MgCl2
- Which one of the following has the greatest Lattice Energy?
- NaCl
- CaCl2
- AlCl3
- KCl
Solutions
- Lattice energy: The difference in energy between the expected experimental value for the energy of the ionic solid and the actual value observed. More specifically, this is the energy gap between the energy of the separate gaseous ions and the energy of the ionic solid.
Ionization energy: The energy change associated with the removal of an electron from a neutral atom or ion.
Electron affinity: The release of energy associated with the addition of an electron to a neutral atom or ion.
- Hess' Law states that the overall energy of a reaction may be determined by breaking down the process into several steps, then adding together the changes in energy of each step.
- Lattice Energy= [-436.68-89-(0.5*158)-418.8-(-328)] kJ/mol= -695.48 kJ/mol
- Lattice Energy= [-641.8-146-243-(737.7+1450.6)-(2*-349)] kJ/mol= -2521.1 kJ/mol
- MgO. It has ions with the largest charge.
- AlCl3. According to the periodic trends, as the radius of the ion increases, lattice energy decreases.
References
- Ralph, William, F.Geoffrey, and Jeffry. General Chemistry. Ninth ed. New Jersey:Pearson Education, Inc. 2007. p500;513-515.
- Combs, Leon. "Lattice Energy". Dr. Leon L. Combs. 1999. erkki.kennesaw.edu/genchem8/ge00002.htm
- Picture of NaCl diagram intro.chem.okstate.edu/1314f0...BornHaber2.GIF
- Housecroft, Catherine E. and Alan G. Sharpe. Inorganic Chemistry. 3rd ed. England: Pearson Education Limited, 2008.174-175.



