5.4.4: NH₃
- Page ID
- 172984
Construct SALCs and the molecular orbital diagram for \(\ce{NH3}\)
This is the first example so far that has more than two pendant atoms and the first example in which the molecule has atoms that lie in three dimensions (i.e., it is not flat). Ammonia is a trigonal pyramidal molecule, with three pendant hydrogen atoms. The three-dimensional shape and the odd number of pendant atoms makes this example more complicated than the previous cases of water, carbon dioxide, and bifluoride. In this case, sketching the shapes (step 5) of pendant atom SALCs is less straightforward; rather, an alternative method, the projection operator method, is preferred for generating pictorial representations of the SALCs.
As in previous examples, it is important to remember that interactions of pendant ligands are dependent on their positions in three-dimensional space. You should consider the positions of the four atoms in ammonia to be essentially fixed in relation to each other. We will walk through the steps used to construct the molecular orbital diagram of ammonia. The first few steps are the same as you've seen before:
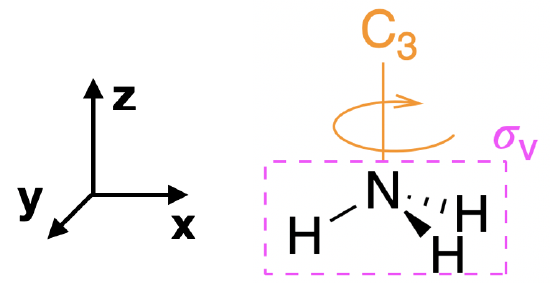
Step 1. Find the point group of the molecule and assign Cartesian coordinates so that z is the principal axis.
The NH\(_3\) molecule is trigonal pyramidal and its point group is \(C_{3v}\). The \(z\) axis is collinear with the principal axis, the \(C_3\) axis.
Step 2. Identify and count the pendant atoms' valence orbitals.
Each of the three pendant hydrogen atoms has one valence orbital; the \(1s\). Thus, we can expect a total of three SALCs from these three atoms.
Step 3. Generate the \(\Gamma\)'s
Use the \(C_{3v}\) character table to generate one reducible representation (\(\Gamma\)); in this case we need only one \(\Gamma\) because there is only one type of valence orbital (the \(1s\)). For each \(s\) orbital, assign a value of 1 if it remains in place during the operation or zero if it moves out of its original place. The \(\Gamma\) is given below:
\[\begin{array}{|c|ccc|} \hline \bf{C_{3v}} & E & 2C_3 & 3\sigma_v \\ \hline \bf{\Gamma_{1s}} & 3 & 0 & 1 \\ \hline \end{array} \nonumber \]
Step 4. Break \(\Gamma\)'s into irreducible representations for individual SALCs
Reduce each \(\Gamma\) into its component irreducible representations. Using either of the processes described previously, we find that the \(\Gamma\) reduces to the two irreducible representations \(A_1\) and \(E\) under the \(C_{3v}\) point group.
\[\begin{array}{|c|ccc|} \hline \bf{C_{3v}} & E & 2C_3 & 3\sigma_v \\ \hline \bf{\Gamma_{1s}} & \bf 3 & \bf 0 & \bf 2 \\
A_{1} & 1 & 1 & 1 \\
E & 2 & -1 & 0 \\
\hline \end{array} \nonumber \]
Notice that we only found TWO irreducible representations. But, in fact we have THREE different SALCs. The \(E\) irreducible representation is doubly degenerate, which in this context means that it corresponds to two degenerate SALCs. Thus, we have already found the symmetries of the three SALCs for ammonia: Two of the SALCs are degenerate with \(E\) symmetry under the \(C_{3v}\) point group, while the third SALC has \(A_1\) symmetry.
Step 5. Sketch the SALCs using the PROJECTION OPERATOR METHOD
From the first four steps (described above), you have found the symmetries (the irreducible representations) of all three SALCs under the \(C_{3v}\) point group. To sketch the SALC that corresponds to each irreducible representation, again we use the \(C_{3v}\) character table. But now we will introduce the projection operator method to derive the surface representation of each SALC.
Step 5.1: Label the pendent atoms
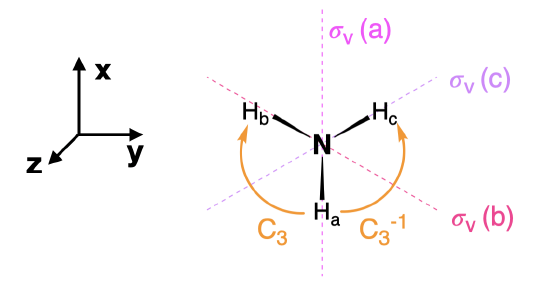
In the projection operator method, first label each of the pendant atoms so that we can distinguish identical atoms from one another; for example, identify the three hydrogen atoms on ammonia as \(H_a\), \(H_b\), and \(H_c\) (Figure \(\PageIndex{2}\)).
Step 5.2: Create an expanded character table with one pendant atom's projected position after each operation
We will perform each operation of the \(C_{3v}\) point group on this labeled molecule and follow where one of the atoms is projected after the operation is complete. We will arbitrarily choose H\(_a\). For example, upon performing the identity operation, E, the H\(_a\) atom is projected onto itself. On the other hand, H\(_a\) is projected onto \(H_b\) upon a clockwise \(C_3\) rotation (as drawn in Figure \(\PageIndex{2}\)). We take into account the result of each operation using an expanded character table (refer to the table below, \ref{expanded1}). In the expanded character table, each operation within each class is written separately (i.e., \(2C_3\) is accounted for separately as \(C_3\) and \(C_3^{-1}\)).
\[\text{Table }\ref{expanded1} \text{: The expanded character table, and the projection of \(H_a\) by each operation is shown below.} \nonumber \]\[\begin{array}{|r|cccccc|} \hline \bf{C_{3v}} & E & C_3 & C_3^{-1} & \sigma_v(a) & \sigma_v(b) & \sigma_v(c) \\ \hline \bf{\text{Projection of }H_a} & H_a & H_b & H_c & H_a & H_c & H_b \\
\hline \end{array} \label{expanded1} \]
Step 5.3: Find the contribution of each pendant atom to each SALC
Next, create a linear combination of the projections for each of the SALCs (the irreducible representations found in step 4). For each of the irreducible representations, multiply the projection by the respective character of the operation.
\[\text{Contribution of each atom to the SALC } = \sum(\text{Projection of }H_a \times \chi) \nonumber \]
The linear combination for all irreducible representations of \(C_3v\) is shown below.
\[\text{Table }\ref{expanded2} \text{: The symmetry adapted linear combination (SALC) for each irreducible representation of \(C_3v\) is shown.} \nonumber \]\[\begin{array}{|r|cccccc|l|} \hline \bf{C_{3v}} & E & C_3 & C_3^{-1} & \sigma_v(a) & \sigma_v(b) & \sigma_v(c) & \text{Linear Combination} \\
\hline \bf{\text{Projection of }H_a} & \bf H_a & \bf H_b & \bf H_c & \bf H_a & \bf H_c & \bf H_b & \\
A_1 & 1 & 1 & 1 & 1 & 1 & 1 & = \bf 2H_a + 2H_b + 2H_c \\
A_2 & 1 & 1 & 1 & -1 & -1 & -1 & = 0 \\
E & 2 & -1 & -1 & 0 & 0 & 0 & = \bf 2H_a - H_b - H_c \\
\hline \end{array} \label{expanded2} \]
Notice that there are only two irreducible representations that produce SALCs, and these are the same that were found in Step 4, above. This illustrates the fact that only the irreducible representations found through the reduction of the \(\Gamma\) will produce SALCs. We can ignore any irreducible representations that were not found in Step 4. Or, you can check your work in Step 4 by applying the projection operator to any irreducible representations not found in Step 4, and finding that they produce a sum of zero.
Step 5.4: Sketch the SALCs
The meaning of the linear combinations found in Table \ref{expanded2} is as follows:
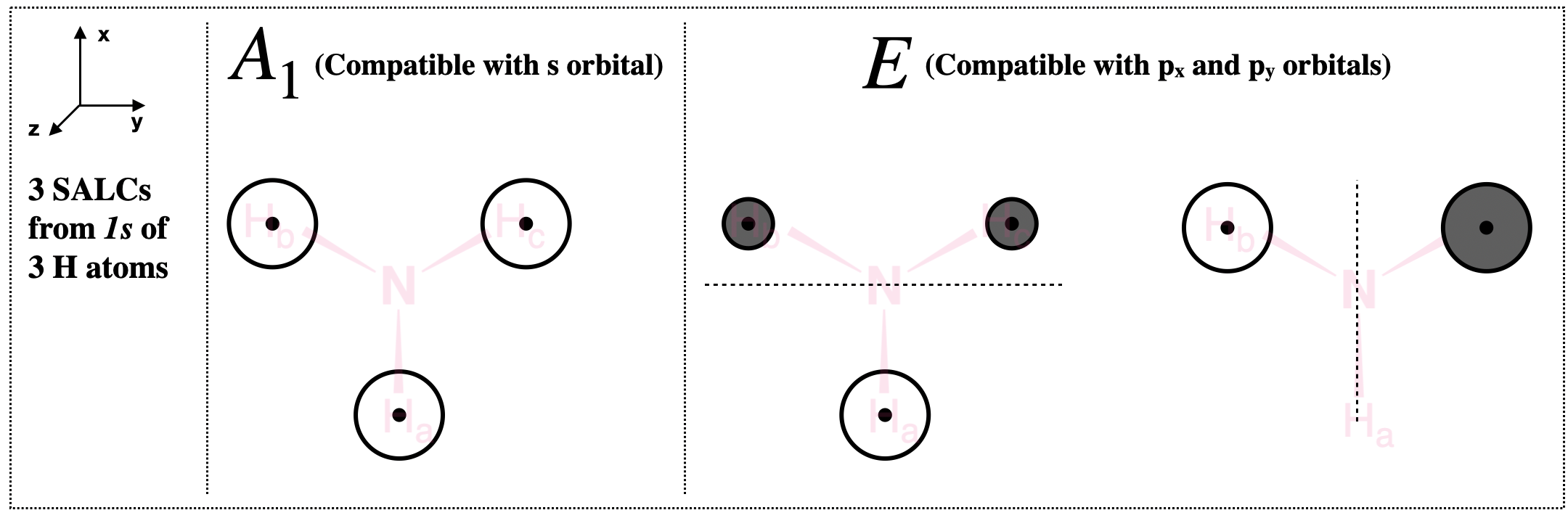
- Sketch the SALC with \(A_1\) symmetry: The linear combination \(2H_a + 2H_b + 2H_c\) indicates all contributions to this SALC are of the same sign (of the wavefunction). Qualitatively, this means there is no node in this SALC. We can take this SALC almost literally to assume that all three H 1s wavefunctions contribute equally to the SALC. We can also use the fact that the \(A_1\) representation possesses the full symmetry of the \(C_3v\) point group, is compatible with an s orbital on N, and thus is a totally symmetric SALC.
Quantitatively, we can apply the normalizing factor, N, for this SALC. The linear combination for the \(A_1\) SALC in Table \ref{expanded2} shows us that the coefficient for each orbital is 1. Thus, the normalizing factor for the \(A_1\) SALC is \(N=\left(\frac{1}{\sqrt{1^2 + 1^2 + 1^2}}\right) = \frac{1}{\sqrt{3}}\). This tells us that \(H_a\), \(H_b\), and \(H_c\) each contribute \(\frac{1}{\sqrt{3}}\) to the normalized \(A_1\) group orbital: \[ A_1 \text{ group orbital } = \frac{1}{\sqrt{3}}\left[\psi_{H_{a}}+\psi_{H_{b}}+\psi_{H_{c}}\right] \nonumber \] This is shown visually in Figure \(\PageIndex{3}\). - Sketch two SALCs with E symmetry: The linear combination \(2H_a - H_b - H_c\) indicates that there are contributions with both positive and negative sign to the wavefunction for each of the \(E\) group orbitals. Qualitatively, this tells us that there is a node within each of these two SALCs, and that the total contribution of the positive portion of the wavefunction is equal to the contribution of the negative portion.
- Finding the first E SALC:
For one of the SALCs, we can take the linear combination from Table \ref{expanded2} almost literally: The contribution from \(H_a\) is equal and opposite to the sum of the contributions from \(H_b + H_c\). This would result in a SALC as shown in Figure \(\PageIndex{3}\) (E, left), that would have symmetry of the \(x\) axis and that would be compatible with the \(p_x\) orbital on N. The node exists in the \(yz\) plane and there is an equal contribution of positive and negative parts of the total wavefunction.
We can also apply the normalizing factor, N, to find this SALC. The linear combination for the \(E\) SALC in Table \ref{expanded2} shows us that the coefficients for orbital contributions are 2, -1, and -1. Thus, the normalizing factor for the first \(E\) SALC is \(N=\left(\frac{1}{\sqrt{2^2 + (-1)^2 + (-1)^2}}\right) = \frac{1}{\sqrt{6}}\). This normalized \(E\) group orbital is: \[\text{First } E \text{ group orbital } = \frac{1}{\sqrt{6}}\left[2\psi_{H_{a}}-\psi_{H_{b}}-\psi_{H_{c}}\right] \nonumber \] This is shown visually in Figure \(\PageIndex{3}\) (E, left). - Finding the second E SALC:
The second SALC is less obvious at first glance. We must use clues from the character table to help us determine what it should "look like". Since the \(E\) representation transforms as the group, (\(x,y\)), we know that one of the SALCs will have the symmetry of the \(x\) axis and \(p_x\) orbital on the central nitrogen atom, while the other should possess the symmetry of the \(y\) axis and be compatible with the \(p_y\) orbital on nitrogen. This alone could lead you to the sketch of the second SALC with E symmetry shown in Figure \(\PageIndex{3}\) (E, right). This second E SALC must have a node in the \(xz\) plane, and because \(H_a\) lies in this node, \(H_a\) cannot contribute to this group orbital. Retaining the fact that the positive and negative contributions of the linear combination must be equal, we can arrive at a SALC that has equal but opposite contributions of \(H_b\) and \(H_c\), and no contribution by \(H_c\) (Figure \(\PageIndex{3}\), right).
We can also apply the normalizing factor, N, to find this SALC. But we must apply the fact that \(H_a\) cannot contribute to the SALC with "\(y\)" symmetry. We remove the contribution of \(H_a\), leaving us with coefficients of 0 for \(H_a\) and \(1\) for \(H_b\) and \(H_c\). Thus, the normalizing factor for the second \(E\) SALC is \(N=\left(\frac{1}{\sqrt{0^2 + 1^2 + 1^2}}\right) = \frac{1}{\sqrt{2}}\). To this, we must add positive and negative coefficients so that the entire wavefunction of this SALC is normalized. The result for this normalized \(E\) group orbital is: \[\text{Second } E \text{ group orbital } = \frac{1}{\sqrt{2}}\left[\psi_{H_{b}}-\psi_{H_{c}}\right] \nonumber \] This is shown visually in Figure \(\PageIndex{3}\).
- Finding the first E SALC:
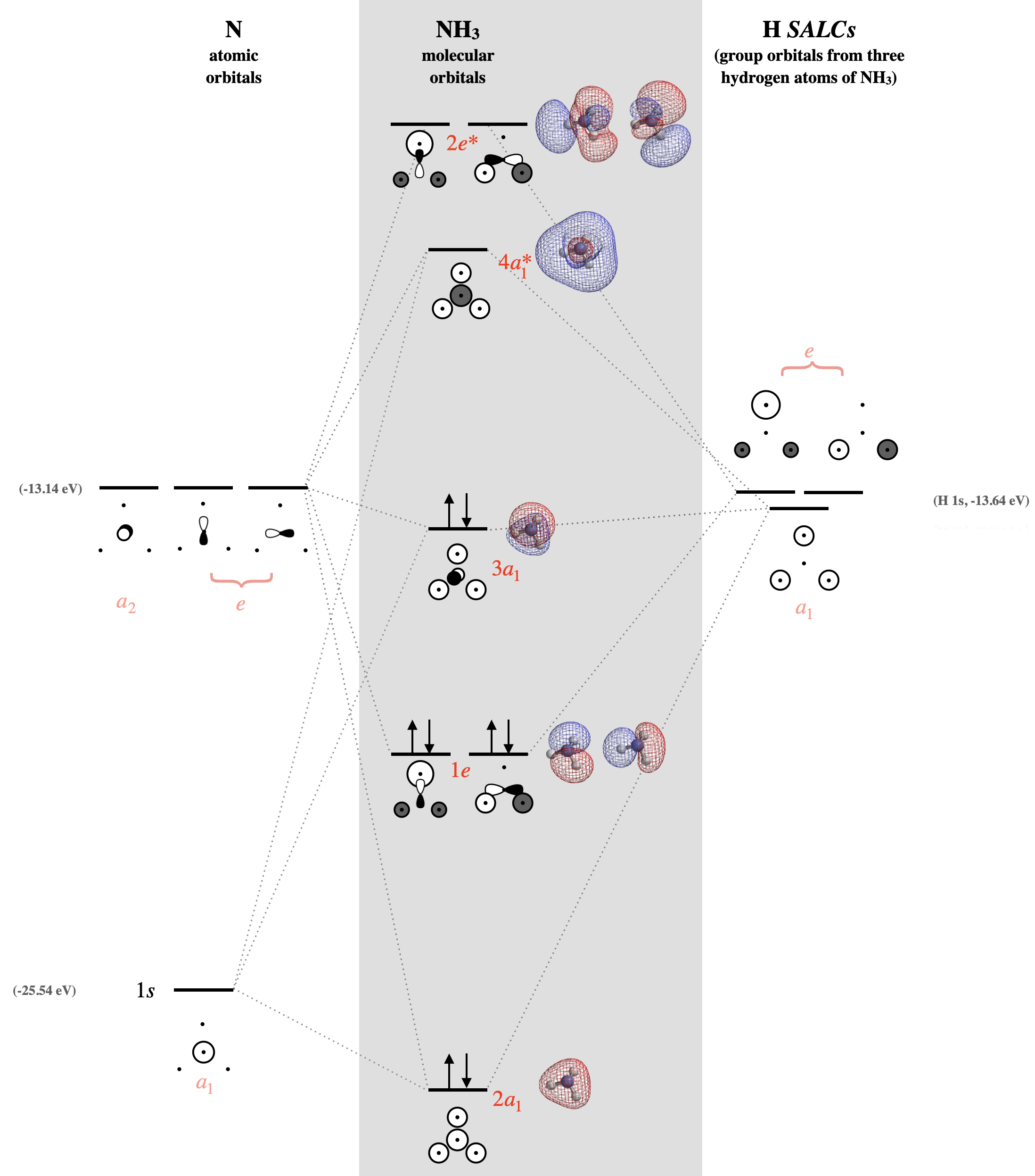
Step 6. Combine SALCs with AO’s of like symmetry to draw the MO diagram for \(\ce{NH_3}\)
First we must identify the valence orbitals on the central nitrogen: there are four including \(2s\), \(2p_x\), \(2p_y\), and \(2p_z\). Now we identify the symmetry of each using the \(C_{3v}\) character table. The symmetry of a central \(2s\) orbital corresponds to the combination of functions \(x^2\), \(y^2\), and \(z^2\) in the character table; this is \(A_1\). The \(p_z\) orbital also corresponds to \(A_1\). And so on... The symmetries of nitrogen valence orbitals are listed below. \[2s =A_1 \\ (2p_x, \; 2p_y) = E \\ 2p_z = A_1 \nonumber \]
The next step is to get a sense of the relative energies of valence atomic orbitals for nitrogen and hydrogen, and then construct the molecular orbital diagram. The nitrogen \(2s\) orbital is about 12 eV lower in energy than a H \(1s\). This difference is an acceptable energy-match for the H orbitals to interact, but would not usually result in a strong interaction. On the other hand, the nitrogen 2p orbitals have an energy very close to the hydrogen 1s, different by only 0.5 eV. Knowledge of the relative energies of the atomic orbitals tells us that, when constructing a diagram, we can place the H SALCs at an energy similar to that of the N \(2p\) orbitals, while the N \(2s\) is much lower (Figure \(\PageIndex{4}\)).
The \(2s\) and \(2p_z\) orbitals have \(A_1\) symmetry and can combine with the \(A_1\) SALC. These orbitals will give three molecular orbitals. The \(2s\) orbital will not have strong interactions with the other orbitals of \(A_1\) symmetry due to the large energy difference. The \(2p_z\) orbital will not have good overlap with the wavefunctions for the three hydrogen orbitals due to their positions in space: The \(2p_z\) orbital has half of its angular distribution pointed away from the hydrogen orbitals, and half pointed toward the center of a triangle formed by the three hydrogen atoms. The nitrogen \(2s\) and \(2p_z\) will combine with the hydrogen SALC of \(A_1\) symmetry to give three molecular orbitals; one low-energy bonding orbital, one mid-energy non-bonding orbital, and one high-energy antibonding orbital. The mid-level non-bonding \(a_1\) molecular orbital is close in energy to, and resembles, the nitrogen \(2p_z\) orbital. The lowest energy \(a_1\) molecular orbital will be lower in energy, but be similar to the nitrogen \(2s\).
The remaining two \(2p\) orbitals are degenerate and possess \(E\) symmetry under the \(C_{3v}\) point group. Although these orbitals are a good energy match, again, their orientation and positions in space do not allow for good orbital overlap, and their bonding and antibonding interactions are relatively weak compared to what we might otherwise expect from such a good energy match. The \(e\) atomic orbitals of nitrogen will combine with the \(e\) SALCs to give a set of two degenerate bonding molecular orbitals and a set of two degenerate antibonding orbitals (four total molecular orbitals of \(e\) symmetry). The MO diagram for \(\ce{NH3}\) is shown in Figure \(\PageIndex{4}\), with calculated electron density surfaces of each MO shown.