1.7: Structure and Bonding - Stereochemistry
- Page ID
- 212840
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Stereo isomers
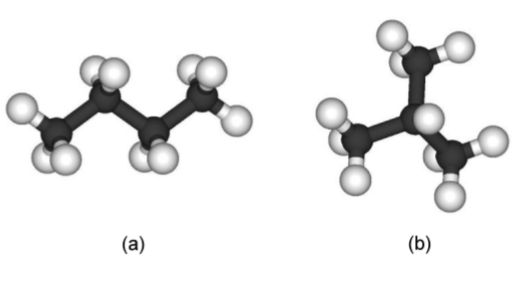
Stereo isomers have the same empirical formula or molecular formula but different structural formulas. A typical example is butane, C4H10, which can have two different possible structures: n-butane (Figure \(\PageIndex{1}\).30a) and iso-butane also known as 1-methylpropane (Figure \(\PageIndex{1}\).30b).
Geometric isomers
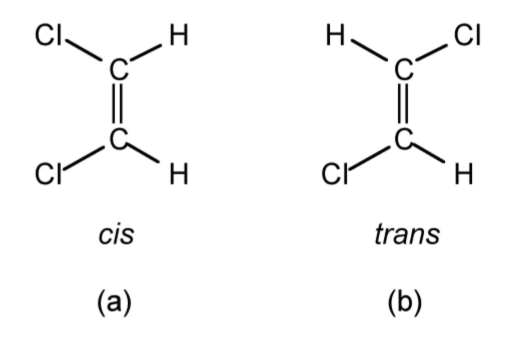
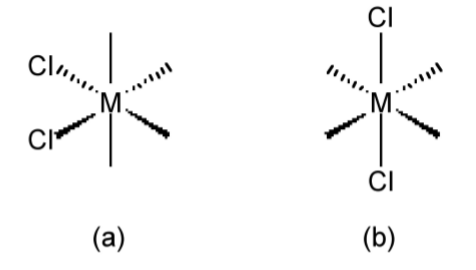
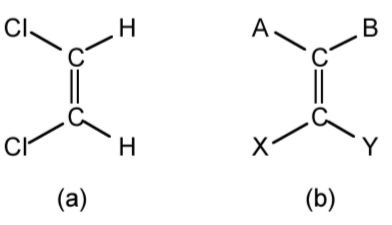
Geometric isomers have the same empirical formula or molecular formula and also the same structural formula, but have a different relative arrangement of the substituent groups. For example, the two geometric isomers of 1,2-dichloroethene (Figure \(\PageIndex{1}\).31) have the molecular formula of C2H2Cl2, and the same structural formula of Cl(H)C=C(H)Cl, but the relative position of the two chlorine atoms can either be the same side of the C=C double bond (i.e., cis, see Figure \(\PageIndex{1}\).31a) or on opposite sides of the C=C double bond (i.e., trans, see Figure \(\PageIndex{1}\).31b). The use of cis and trans is not limited to organic compounds such as olefins, but can also be used in metal complexes, e.g., Figure \(\PageIndex{1}\).32.
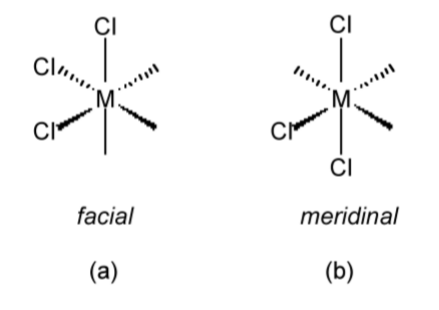
When it is not possible to describe geometric isomers by the terms cis or trans, the terms facial (fac, Figure \(\PageIndex{1}\).33a) or meridinal (mer, Figure \(\PageIndex{1}\).33b) are commonly employed.
Optical isomers
If the mirror object and mirror image of a molecule are not the same (i.e., they are not superimposable) they are known as enantiomers. If they also have optical activity they are called chiral and are described as having chirality. Enantiomers of a particular compound have the same general properties with two exceptions:
- Their behavior to polarized light.
- Their reaction with other chiral molecules
It is possible to determine if a molecule is chiral or not from its symmetry. Chiral molecules will have no symmetry or axis of rotation. The optical activity of a chiral molecule will turn the plane of polarized light either to the right (+) or the left (-). The former is known as dextrorotatory (D), while the latter is known as levorotatory (L).
Configuration
The configuration of a chiral molecule may be represented in a number of ways. Lactic acid (C3H6O3) provides a suitable and simple example. The two optical isomers of lactic acid can be represented in 3-dimensional (3D) form as shown in Figure \(\PageIndex{1}\).34; however, it is also possible to draw the same molecules in 2D using the Fischer projection (Figure \(\PageIndex{1}\).35). While the Fisher projection does not appear to dene the geometry about the central carbon atom, the convention is that the side chains are out of the plane of the page (towards the observer), while the top and bottom groups are into the plane of the page (away from the observer). Thus, Figure \(\PageIndex{1}\).35a is a representation of Figure \(\PageIndex{1}\).34a, and Figure \(\PageIndex{1}\).35b is a representation of Figure \(\PageIndex{1}\).34b.
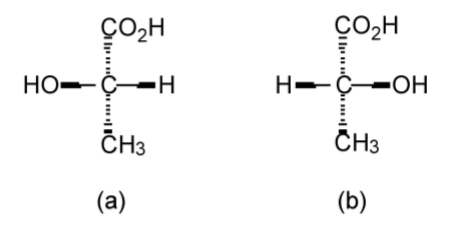
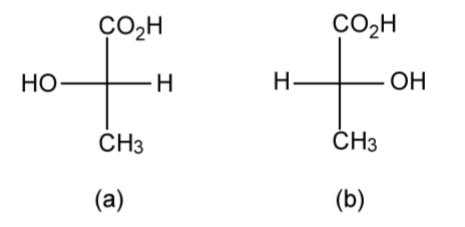
Fischer-Rosenoff convention
The Fischer-Roseno convention defines chirality of a molecule using the Fischer projection. The convention is based upon D-(+)-glyceraldehydes (Figure \(\PageIndex{1}\).36).
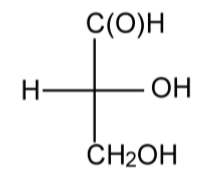
To determine the chiral label for a molecule, the Fischer projection is drawn with the longest carbon chain pointing away from the observer, i.e., into the plain of the page. The number 1 carbon (that of the highest substitution) is positioned at the top of the diagram. If the functional group is on the right of the diagram the isomer is given the label D (from the dextrorotatory enantiomer of glyceraldehydes rather than the molecule being dextrorotatory per se), i.e., Figure \(\PageIndex{1}\).36. On the other hand if the functional group is on the left of the diagram the isomer is given the label L (from the levorotatory enantiomer of glyceraldehyde rather than the molecule being levorotatory per se).
Rules
Where molecules are large and complex a number of additional rules are useful:
- Make any alcohol substituent to be nearest to the top, e.g., a butan-2-ol (Figure \(\PageIndex{1}\).37a) rather than a butan-3-ol (Figure \(\PageIndex{1}\).37b).
- Aldehydes and ketones are the number 1 carbon atom.
- If there are both sets of substituents, rule 1 has precedence over rule 2.
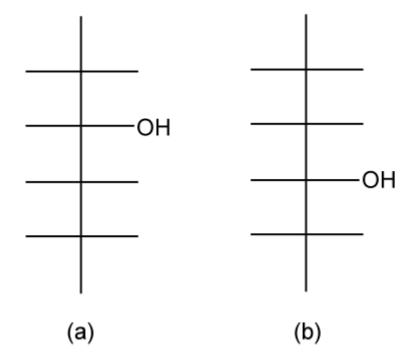
Nomenclature in terms of R and S
The R/S nomenclature is a more widely used alternative to the D/L nomenclature, and is based upon the hierarchical order of the substituents. From the Fischer projection, the groups are ordered with the largest atom first, as shown in Figure \(\PageIndex{1}\).38. The lowest numbered substituent is then oriented away from the observer (i.e., H in Figure \(\PageIndex{1}\).38). The order of the remaining substituents 1, 2, 3 is then traced: if it goes clockwise the molecule is labeled R, if it goes anti-clockwise (counter-clockwise) the molecule is labeled S.
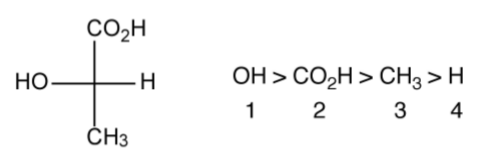
The advantage of the R/S methodology is that it can also be used for geometric isomers. Thus, while cis and trans are useful when the groups either side of a C=C double bond are the same (e.g., cis-1,2dichloroethene, Figure \(\PageIndex{1}\).39a); however, when four different groups are present (e.g., A, B, X, and Y as seen in Figure \(\PageIndex{1}\).39b) then an alternative must be used. By taking either group A/B or X/Y and placing in order of precedence, the relative order defines the isomer. Thus, if in Figure \(\PageIndex{10}\)b A>B and X>Y the label Z (zusammen from the German for together) is used. Conversely, if in Figure \(\PageIndex{10}\)b A<B and X>Y the label E (entgegen from the German for opposite) is used.
More complex molecules
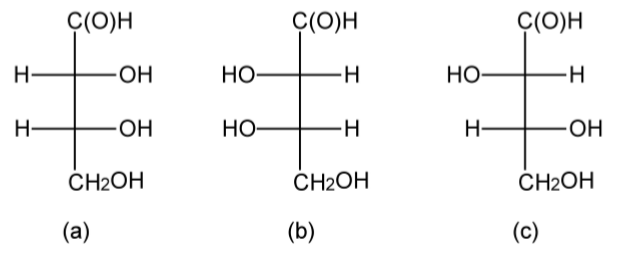
As molecules become more complex with multiple functional groups and multiple chiral centers the D/L nomenclature has the potential to become confusing. Erythrose has two chiral centers, and based upon the Fischer projections it may be seen that since the alcohol substituents in the 2 and 3 positions are on the same side of the backbone in the Fischer projection irrespective if it is D-(-)-erythrose or L-(+)-erythrose (Figure \(\PageIndex{1}\).40a and b). Thus, the naming is simplified despite the presence of multiple side groups. However, in threose (Figure \(\PageIndex{1}\).40c) the substituents are on different sides of the Fischer projection raising the issue as to whether this should be L or D. However, in such cases the substituent at the bottom of the side chain takes priority, thus Figure \(\PageIndex{1}\).40c is D-(-)-threose.
Note
D-(-)-erythrose and L-(+)-erythrose are enantiomers, and D-(+)-threose and L-(+)-threose are also enantiomers, but threose and erythrose are diasteriomers. Enantiomers have the same physical properties (just different behavior to polarized light), while diasteriomers may have different physical properties such as melting points and solubility.
Amino Acids
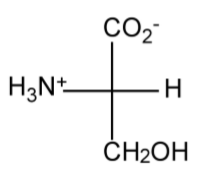
Amino acids (or more properly α-amino acids) are compounds containing both an amine (NH2) group and a carboxylic acid (CO2H) attached to the same carbon atom. The presence of both acid and base groups can result in the formation of the Zwitterionic form with ammonium (NH3+) and carboxylate (CO2-) groups.
In defining the labels for amino acids, the basis is D-(-)-allothreonine (Figure \(\PageIndex{1}\).41), whereas for an amino acid such as threonine the top substituent is used for a label, e.g., Figure \(\PageIndex{1}\).42.
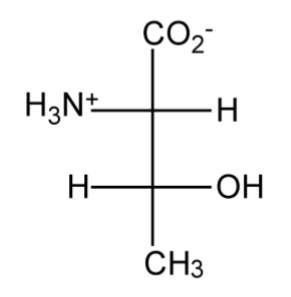
Similar chiral centers
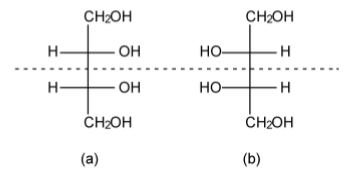
Just because a compound has more than one chiral center does not mean that it is optically active. A consideration of erythritol shows the presence of a mirror plane of symmetry (Figure1.43). As such, erythritol is not optically active, i.e., there is no effect on polarized light. In contrast, while threitol has the same molecular and geometric formula, the lack of a mirror plane of symmetry (Figure \(\PageIndex{1}\).44) means that the L- and D+ forms are optically active.
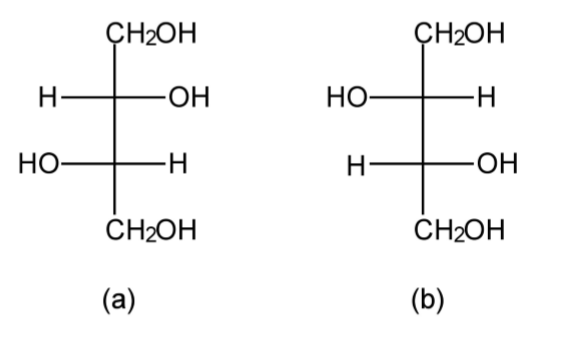
Compounds with a D:L ratio of 1:1 are called racemic compounds and are totally optically inactive. However, it is also possible for a racemic solution of a compound to crystallize to form crystals of pure D or L, which may be manually separated.
Optical isomers that are not tetrahedral
Pyrimidal molecules
Pyramidal molecules can also exhibit chirality when the three substituents are distinct, e.g., PR1R2R3 (Figure \(\PageIndex{1}\).45). Unfortunately, most pyramidal compounds undergo an inversion of their isomers (in a similar manner to turning an umbrella inside out), such that the chiral forms interconvert rapidly. In such a case, it is not possible to resolve (separate) the different forms. Phosphines may generally be resolved because the barrier to their inversion is suficiently large (ca. 132 kJ/mol)
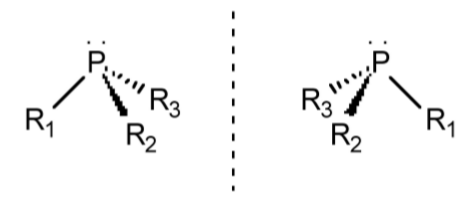
The notation used for pyramidal molecules is the same as that for tetrahedral molecules, in that the individual substituents are ordered with the largest atom first. The lone pair is defined as having the lowest numbering and thus is oriented away from the observer. The order of the remaining substituents 1, 2, and 3 is then traced: if it goes clockwise the molecule is labeled R, if it goes anti-clockwise (counter-clockwise) the molecule is labeled S.
Chirality in octohedral complexes
The presence of a chelate ligand on an octahedral complex can induce chirality in the complex.
Note
A chelate ligand is a molecule or ion that is bonded to at least two points of a central atom or ion. The term chelate is from the Greek chelè, meaning claw.
Unlike tetrahedral based compounds, chiral octahedral compounds have their nomenclature based on the structure of a helix. For example, in the case of a bis-chelate complex (Figure \(\PageIndex{1}\).46), with one of the chelate ligands pointing straight up the helix, the direction of the other defines the chirality of the helix, i.e., if it is a left or right hand helix. If the ligand points up to the left the complex is assigned the symbol shown in Figure \(\PageIndex{1}\).46a, while if the ligand points up to the right the complex is assigned the symbol shown in Figure \(\PageIndex{1}\).46b.
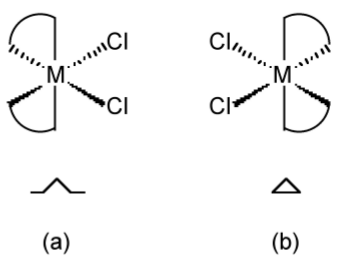
In complexes with three chelate ligands (i.e., a tris-chelate complex, Figure \(\PageIndex{1}\).47), the same methodology applies, in that any two ligands can be chosen and the same rules applied.
Methods of resolution of racemic mixtures
A racemic mixture, or racemate, is one that has equal amounts of left- and right-handed enantiomers of a chiral molecule. The first known racemic mixture was "racemic acid," which Louis Pasteur (Figure \(\PageIndex{1}\).48) found to be a mixture of the two enantiomeric isomers of tartaric acid (Figure \(\PageIndex{1}\).49).

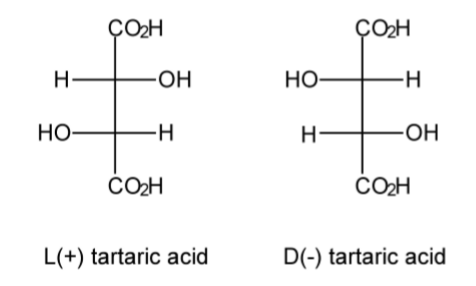
In nature, it is common that only one of an optical isomers is naturally produced, but in laboratory synthesis it is more common that both isomers are made in equal amounts. The separation of a racemate into its components (the pure enantiomers) is called a chiral resolution.
Mechanical seperation
The crystals of enantiomerically pure compounds often have different appearances. Thus, just as Pasteur did in 1848, it is often possible to look under a microscope and physically separate the two different enantiomers.
Resolution by formation of diasteriomers
One of the differentiating properties of a chiral molecule is that each enantiomer reacts with another chiral molecule to form a diastereomeric pair of compounds. For example, a racemic acid, (+)HA and (-)HA, will react with a chiral base, (-)B, to form a mixture of diasteriomers, [(-)BH+.(+)A-] and [(-)BH+.(-)A-]. Because diasteriomers have different physical properties they can be separated by recrystallization. Once separated by recrystallization, the addition of excess acid will liberate the enantiomerically pure compound, i.e., (+)HA or (-)HA. A typical chiral base would be a natural alkaloid base to ensure that it is pure + or -. If it is a base that is needed to be separated, then (-)malic acid is a suitable acid.
Resolution by chromatography
In a related method to resolution by the formation of diasteriomers, a chiral column material will allow for the chromatographic separation of an enantiomeric mixture. Thus, the retention rate for (+)X will be different from (-)X on a column in which the stationary phase is chiral, i.e., (-)A. Many common chiral stationary phases are based on oligosaccharides such as cellulose or cyclodextrin (in particular with β-cyclodextrin).
Labile stereo isomers and racemization
It is only possible to separate (resolve) racemic mixtures if the molecule stays as one form for a long time. In other words, if there is a mechanism by which the two forms are interconverted, then resolution cannot be achieved.
Intramolecular rearrangement
Intramolecular rearrangements involve no bonds being broken. The classic example is the inversion of an amine, (1.12), which has a low energy barrier (24.7 kJ/mol).

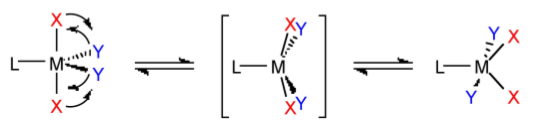
Another example of an intramolecular rearrangement is the conversion of a square-based pyramidal geometry via a trigonal bipyramidal geometry to the isomeric square-based pyramidal geometry, or the alternative isomerization of one trigonal bipyramidal geometry to another via a square-based pyramidal transition state. Such a process is known as a Berry rotation. The Berry mechanism is a pseudorotation process for simultaneously interchanging two equatorial groups with the two axial groups, while the third equatorial group (called the pivot group) remains an equatorial group (Figure \(\PageIndex{1}\).50).
Intermolecular processes
Intermolecular processes involve bond breaking (and bond formation). For example a tetrahedral compound could loose one ligand, which creates a labile pyramidal compound. Rapid inversion of the pyramidal compound is followed by re-attachment of the ligand. Such a process is often so fast that resolution cannot be achieved.
Intramolecular processes
Intramolecular processes with bond breaking (and making) also lead to racemization. For example, in an octahedral complex with chelate ligands, if one of the ends of a chelate ligand detaches, it can reattach in the same configuration, or attach differently to change the chirality. In this manner the chirality can be changed from one form to another.
Conformation
The conformation of a molecule arises from the rotation of a single bond (Figure \(\PageIndex{1}\).51). However, even though there is rotation about the bond, there are energy barriers due to steric interactions of the substituents. In order to understand (and predict) these interactions, it is necessary to visualize the molecule in such a manner as to highlight the across-bond interactions; this is done by using a Newman projection.
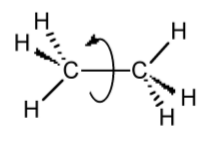
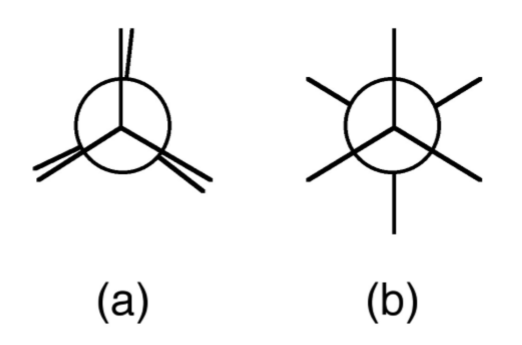
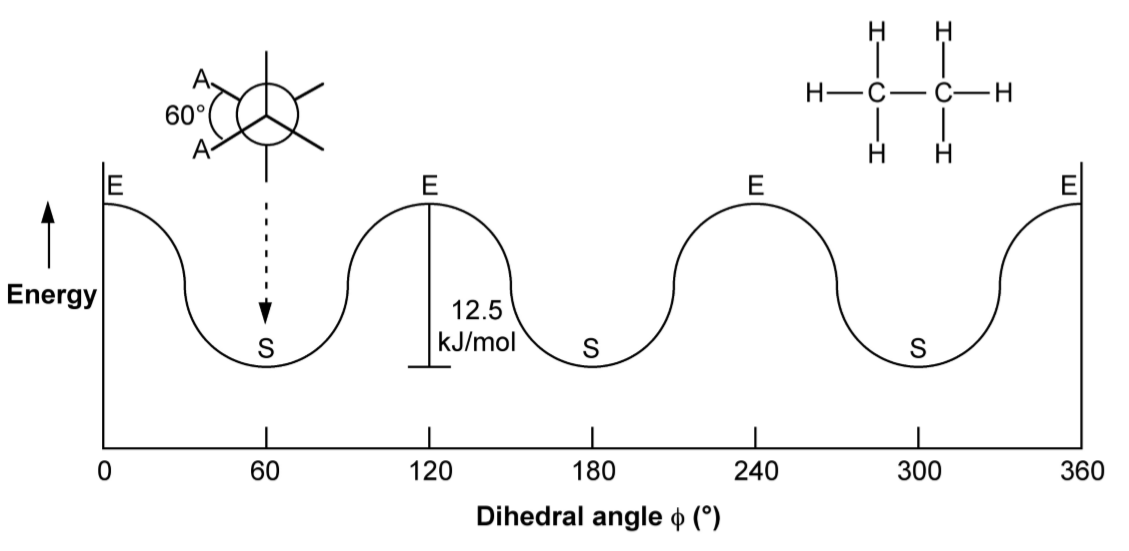
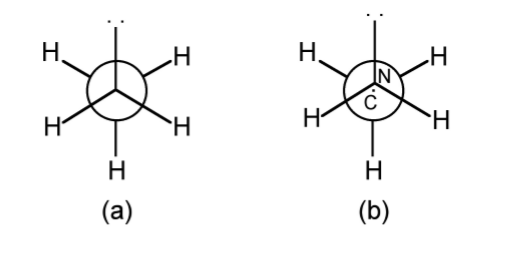
A Newman projection, useful in alkane stereochemistry, visualizes chemical conformations of a carbon-carbon chemical bond from front to back, with the front carbon represented by a dot and the back carbon as a circle (Figure \(\PageIndex{1}\).52). The front carbon atom is called proximal, while the back atom is called distal. This type of representation is useful for assessing the torsional angle between bonds. Using ethane as an example, the Newman projection along the C-C single bond results in two basic conformations: eclipsed (Figure \(\PageIndex{1}\).52a) and staggered (Figure \(\PageIndex{1}\).52b). The staggered conformation will be energetically favored since the substituents are the most distant from each other. Conversely, the staggered will be the highest in energy. The difference in energy between the two conformations will define the barrier to rotation. In the case of ethane this is very small (12.5 kJ/mol).
Although we often only consider the two extreme conformations, in reality there is a continuum around 360◦ rotation of the C-C bond. Figure \(\PageIndex{1}\).53 shows the relative energy as a function of the dihedral angle for ethane. Since each carbon in ethane has equivalent substitution (i.e., three H atoms) the energy for each staggered conformation is the same. This is not true for more complex molecules such as butane (Figure \(\PageIndex{1}\).54).
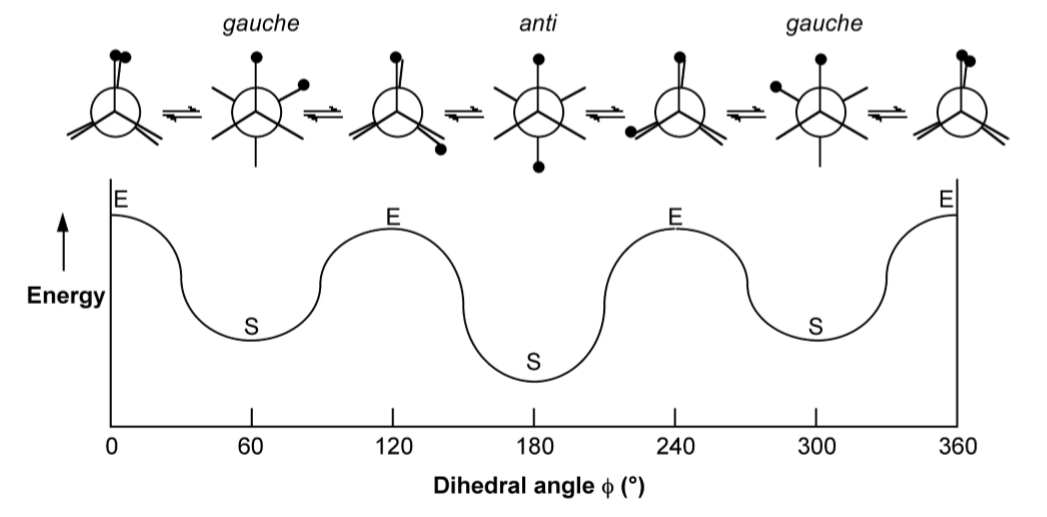
As may be seen from Figure \(\PageIndex{1}\).54, the staggered conformation in which the two methyl groups (represented by the black circles) are as far away from each other (anti) is the most energetically favored. The other two staggered conformations (gauche) are mirror images of each other and are hence conformation enantiomers. It should also be noted from Figure \(\PageIndex{1}\).54 that the eclipsed conformations vary in energy since the presence of methyl...methyl near neighbors is clearly less energetically favorable than methyl...H near neighbors.
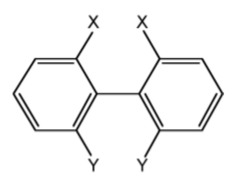
Generally the rotation about C-C bonds has a low barrier to rotation, however, if substituents are suciently bulky the molecule will not twist around the bond, e.g., substituted bi-phenyl with sterically bulky substituents (Figure \(\PageIndex{1}\).55).
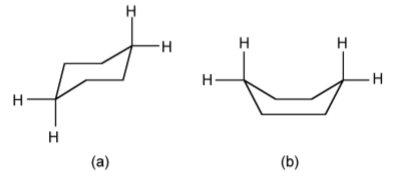
Free rotation about a C-C bond is not fully possible when you have a ring system, e.g., in a cyclic compound such as cyclohexane, C6H12. The limited rotation about the C-C bonds results in the ipping of the ring conformation from the chair form (Figure \(\PageIndex{1}\).56a) to the boat form (Figure \(\PageIndex{1}\).56b). Since the boat form has steric hindrance between the hydrogen atoms, the chair form is the more stable.
Conformation of compounds with lone pairs
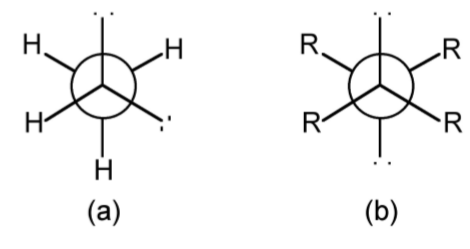
Lone pairs often behave in a different manner to substituents in regard to conformations. Thus, methylamine (CH3NH2) would be predicted to have the staggered conformation shown in Figure \(\PageIndex{1}\).57a. However, the lower steric bulk of the lone pair results in the nitrogen being 0.09 Å away from the true center of the CH3 projection (Figure \(\PageIndex{1}\).57b).
In compounds with more than one lone pair, the lowest energy form is not always the anti conformation. For example, at 20 ◦C hydrazine (H2NNH2) is 100% gauche (Figure \(\PageIndex{1}\).58a); but for substituted hydrazines (i.e., a diamine, R2NNR2) if the substituent groups are suficiently large then the anti conformation will dominate (Figure \(\PageIndex{1}\).58b).
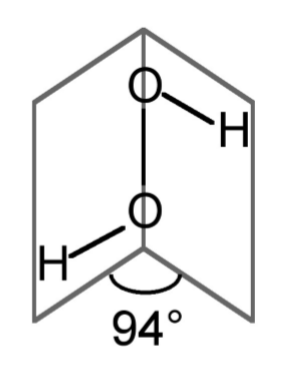
The conformation of hydrogen peroxide (H2O2) is dominated by the lone pairs rather than the hydrogen atoms. Instead of the expected anti conformation (c.f., Figure \(\PageIndex{1}\).54 where the black circles would represent the hydrogen atoms) in the free state the dihedral angle is 94◦ (Figure \(\PageIndex{1}\).59). The conformation of hydrogen peroxide is therefore neither eclipsed nor staggered but an intermediate structure. When in the solid state hydrogen bonding will cause the shape and angles to change.
Bibliography
- R. S. Berry, J. Chem. Phys., 1960, 32, 933.
- A. Keys, S. G. Bott, and A. R. Barron, J. Chem. Cryst., 1998, 28, 629.


