2.1: Operations

Point groups and their operations are denoted by two different but related symbolisms. The Schönflies notation is preferred by molecular chemists because the point group symbol conveys information localized for a single molecule. The International or Hermann-Mauguin notation, on the other hand, is used by crystallographers because the symbol contains information about molecular symmetry relative to an external coordinate system like the unit cell directions of a crystal. Although both notations effectively describe structural symmetry of molecules and solids, they differ in how improper rotations are defined. The following table summarizes the two symbolisms for point group operations and some important relationships:

Table 1. Proper Rotations

Operation	Schönflies Notation			International Notation
By angle 2π/n	\(C_{n}:\)	e.g., \(C_{2},\ C_{3},\ldots\)		\(n:\)	e.g., \(2,\ 3,\ \ldots\)
By angle 2πj/n	\({C_{n}}^{j}:\)	e.g., \({C_{3}}^{2},\ {C_{4}}^{3},\ldots\)		\(n^{j}:\)	e.g., \(3^{2},\ 4^{3},\ \ldots\)
Identity	\(E = C_{1}\)			\(1\)
Properties:	\({C_{n}}^{n} = E\)			\(n^{n} = 1\)
	\({C_{n}}^{n/2} = C_{2}\ (n\ {\rm even})\)			\(n^{n/2} = 2\ (n\ {\rm even})\)
	\({C_{n}}^{- 1} = {C_{n}}^{n - 1}\)			\(n^{- 1} = n^{n - 1}\)

Table 2. Improper Rotations

Operation	Schönflies Notation			International Notation
	Roto-reflections			Roto-inversions
By angle 2π/n	\(S_{n} = \sigma_{h} \cdot C_{n} = C_{n} \cdot \sigma_{h}\):\) e.g., \(S_{3},\ S_{4},\ldots\)			\(\overline{n} = \overline{1} \cdot n = n \cdot \overline{1}:\) e.g., \(\overline{3},\ \overline{4},\ \ldots\)
By angle 2πj/n	\({S_{n}}^{j}:\) e.g., \({S_{3}}^{5},\ {S_{4}}^{3},\ldots\)			\({\overline{n}}^{j}:\) e.g., \({\overline{3}}^{5},{\ \overline{4}}^{3},\ \ldots\)
Inversion	\(i = S_{2}\)			\(\overline{1}\)
Reflections	\(\sigma_{h} = S_{1}\) (⊥ principal rotation axis) \(\sigma_{v} = S_{1}\) (|| principal axis) \(\sigma_{d} = S_{1}\) (|| principal axis)			\(/m = \overline{2}\) (⊥ rotation axis) \(m = \overline{2}\) (|| rotation axis)
Properties	\({\sigma_{h}}^{2} = {\sigma_{v}}^{2} = {\sigma_{d}}^{2} = i^{2} = E\)			\(m^{2} = {\overline{1}}^{2} = 1\)
	\({S_{n}}^{j} = {\sigma_{h}}^{j} \cdot {C_{n}}^{j}\)			\({\overline{n}}^{j} = {\overline{1}}^{j} \cdot n^{j}\)
	\({S_{n}}^{n} = E\ (n\ {\rm even});\ \ {S_{n}}^{2n} = E\ (n\ {\rm odd})\)			\({\overline{n}}^{n} = 1\ (n\ {\rm even});\ \ {\overline{n}}^{2n} = 1\ (n\ {\rm odd})\)
	\({S_{n}}^{n} = \sigma_{h}\ (n\ {\rm odd})\)			\({\overline{n}}^{n} = \overline{1}\ (n\ {\rm odd})\)

Every improper rotation is the product of a proper rotation and a fundamental (1^st-order) improper rotation. In the Schönflies notation, the 1^st-order improper rotation \(S_{1}\) is a reflection, symbolized by \(\sigma\), and improper rotations are roto-reflections. The 2^nd-order operation \(S_{2}\) is inversion through the origin, symbolized by \(i\). In the International notation, the 1^st-order improper rotation \(\overline{1}\) is inversion, so that improper rotations are roto-inversions. The symbol \(\overline{n}\) is read “bar n” or “n bar”. Likewise, the 2^nd-order improper rotation \(\overline{2}\) is a reflection, symbolized by \(m\).

Rotations of either type move objects (functions) from one point \(\mathbf{r}\) to another \(R\mathbf{r}\). To identify the outcome \(R\mathbf{r}\), it is important to recognize that different rotation operations are defined relative to specific symmetry elements: inversion (\(i = \overline{1}\)) is defined relative to a single point; a proper rotation (\(C_{n} = n\); \(n \geq 2)\) is defined relative to an axis or line; and a reflection (\(\sigma = m\)) is defined with respect to a plane. The symmetry elements for any point group intersect in at least one point called the origin. As a result, every rotation \(R\) is represented by a 3×3 matrix. The general position \(\mathbf{r}\) is expressed by a 3×1 column matrix of its Cartesian coordinates and the outcome \(R\mathbf{r}\) is another 3×1 column matrix arising from the rule of matrix multiplication:

\[R\mathbf{r} = \begin{pmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \\ \end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = \begin{pmatrix} R_{11}x + R_{12}y + R_{13}z \\ R_{21}x + R_{22}y + R_{23}z \\ R_{31}x + R_{32}y + R_{33}z \\ \end{pmatrix} \nonumber \]

Expressions for proper and improper rotations with respect to the Cartesian coordinate system are:

Identity:

\[E = 1 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \nonumber \]

Inversion:

\[i = \overline{1} = \begin{pmatrix} - 1 & 0 & 0 \\ 0 & - 1 & 0 \\ 0 & 0 & - 1 \\ \end{pmatrix} \nonumber \]

Proper Rotations (subscript = axis):

\[C_{nz} = n_{z} = \begin{pmatrix} \cos\frac{2\pi}{n} & {- \sin}\frac{2\pi}{n} & 0 \\[6pt] \sin\frac{2\pi}{n} & {\cos}\frac{2\pi}{n} & 0 \\[6pt] 0 & 0 & 1 \\ \end{pmatrix} \nonumber \]

\[C_{nx} = n_{x} = \begin{pmatrix} 1 & 0 & 0 \\[6pt] 0 & \cos\frac{2\pi}{n} & {- \sin}\frac{2\pi}{n} \\[6pt] 0 & \sin\frac{2\pi}{n} & {\cos}\frac{2\pi}{n} \\ \end{pmatrix} \nonumber \]

\[C_{ny} = n_{y} = \begin{pmatrix} {- \cos}\frac{2\pi}{n} & 0 & \sin\frac{2\pi}{n} \\[6pt] 0 & 1 & 0 \\[6pt] {- \sin}\frac{2\pi}{n} & 0 & \cos\frac{2\pi}{n} \\ \end{pmatrix} \nonumber \]

Figure 2.1 (left): \(C_{nz} = n_{z}\), Figure 2.2: (middle) \(C_{nx} = n_{x}\), Figure 2.3: (right) \(C_{ny} = n_{y}\)

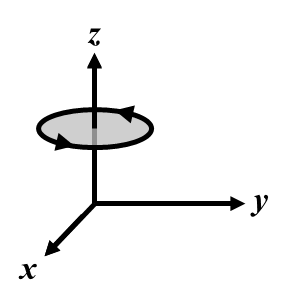
Reflections (subscript = direction perpendicular to the plane):

\[\sigma_{z} = m_{z} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & - 1 \\ \end{pmatrix} \nonumber \]

\[\sigma_{x} = m_{x} =\begin{pmatrix} - 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \nonumber \]

\[\sigma_{y} = m_{y} =\begin{pmatrix} 1 & 0 & 0 \\ 0 & - 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \nonumber \]

Figure 2.4 (left): \(\sigma_{z} = m_{z}\), Figure 2.5: (middle) \(\sigma_{x} = m_{x}\), Figure 2.6: (right) \(\sigma_{y} = m_{y}\)

Improper Rotations (subscript = axis):

\[S_{nz} = \sigma_{z} \cdot C_{nz} =\begin{pmatrix} \cos\frac{2\pi}{n} & {- \sin}\frac{2\pi}{n} & 0 \\[3pt] \sin\frac{2\pi}{n} & {\cos}\frac{2\pi}{n} & 0 \\[3pt] 0 & 0 & - 1 \\ \end{pmatrix} \nonumber \]

\[{\overline{n}}_{z} = \overline{1} \cdot n_{z} = \begin{pmatrix} {- \cos}\frac{2\pi}{n} & {\sin}\frac{2\pi}{n} & 0 \\[3pt] {- \sin}\frac{2\pi}{n} & {- \cos}\frac{2\pi}{n} & 0 \\[3pt] 0 & 0 & - 1 \\ \end{pmatrix}; \nonumber \]

\[S_{nx} = \sigma_{x} \cdot C_{nx} =\begin{pmatrix} - 1 & 0 & 0 \\[3pt] 0 & \cos\frac{2\pi}{n} & {- \sin}\frac{2\pi}{n} \\[3pt] 0 & \sin\frac{2\pi}{n} & {\cos}\frac{2\pi}{n} \\ \end{pmatrix} \nonumber \]

\[{\overline{n}}_{x} = \overline{1} \cdot n_{x} = \begin{pmatrix} - 1 & 0 & 0 \\[3pt] 0 & {- \cos}\frac{2\pi}{n} & {\sin}\frac{2\pi}{n} \\[3pt] 0 & {- \sin}\frac{2\pi}{n} & {- \cos}\frac{2\pi}{n} \\ \end{pmatrix} \nonumber \]

\[S_{ny} = \sigma_{y} \cdot C_{ny} =\begin{pmatrix} {\cos}\frac{2\pi}{n} & 0 & \sin\frac{2\pi}{n} \\[3pt] 0 & - 1 & 0 \\[3pt] {- \sin}\frac{2\pi}{n} & 0 & \cos\frac{2\pi}{n} \\ \end{pmatrix} \nonumber \]

\[{\overline{n}}_{y} = \overline{1} \cdot n_{y} =\begin{pmatrix} {- \cos}\frac{2\pi}{n} & 0 & {- \sin}\frac{2\pi}{n} \\[3pt] 0 & - 1 & 0 \\[3pt] {\sin}\frac{2\pi}{n} & 0 & {- \cos}\frac{2\pi}{n} \\ \end{pmatrix} \nonumber \]

These matrices indicate one important difference between proper and improper rotations: the determinants of the respective matrices are +1 for proper and –1 for improper rotations. As a result, if the object can be characterized by handedness, like the difference between left and right hands, then proper rotations retain handedness whereas improper rotations change handedness.

Example \(\PageIndex{1}\)

Compare the roto-reflection \(S_{4}\) and the roto-inversion \(\overline{4}\) by evaluating the positions \(S_{4}^{j}\mathbf{r}\) and \({\overline{4}}^{j}\mathbf{r}\) for j = 1, 2, 3, and 4. Let the four-fold axis be the z-axis.

Solution

Roto-Reflection \(S_{4z} = \sigma_{z} \cdot C_{4z}\)

Figure 2.7: Effects of S4 roto-reflection operating on a comma at point r = (x,y,z) and looking down the z-axis.  

\[S_{4z}\mathbf{r} = \begin{pmatrix} 0 & - 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & - 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = \begin{pmatrix} - y \\ x \\ - z \\ \end{pmatrix} \nonumber \]

\[S_{4z}^{2}\mathbf{r} = \begin{pmatrix} - 1 & 0 & 0 \\ 0 & - 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = C_{2z}\mathbf{r} = \begin{pmatrix} - x \\ - y \\ z \\ \end{pmatrix} \nonumber \]

\[S_{4z}^{3}\mathbf{r} = \begin{pmatrix} 0 & 1 & 0 \\ - 1 & 0 & 0 \\ 0 & 0 & - 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = \begin{pmatrix} y \\ - x \\ - z \\ \end{pmatrix} \nonumber \]

\[S_{4z}^{4}\mathbf{r} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = E\mathbf{r} = \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} \nonumber \]

Roto-Inversion \({\overline{4}}_{z} = \overline{1} \cdot 4_{z}\)

Figure 2.8: Effects of 4-bar roto-inversion operating on a comma at point r = (x,y,z) and looking down the z-axis. 

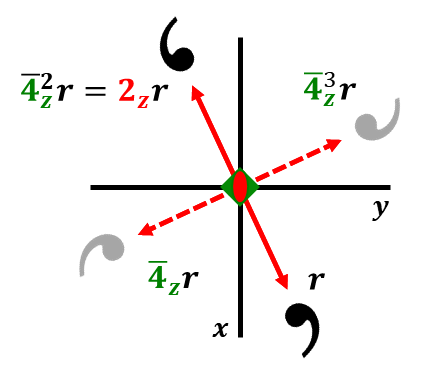
\[{\overline{4}}_{z}\mathbf{r} = \begin{pmatrix} 0 & 1 & 0 \\ - 1 & 0 & 0 \\ 0 & 0 & - 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = \begin{pmatrix} y \\ - x \\ - z \\ \end{pmatrix} \nonumber \]

\[{\overline{4}}_{z}^{2}\mathbf{r} = \begin{pmatrix} - 1 & 0 & 0 \\ 0 & - 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = 2_{z}\mathbf{r} = \begin{pmatrix} - x \\ - y \\ z \\ \end{pmatrix} \nonumber \]

\[{\overline{4}}_{z}^{3}\mathbf{r} = \begin{pmatrix} 0 & - 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & - 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = \begin{pmatrix} - y \\ x \\ - z \\ \end{pmatrix} \nonumber \]

\[{\overline{4}}_{z}^{4}\mathbf{r} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = 1\mathbf{r} = \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} \nonumber \]

The two sets \(\left\{ S_{4},{S_{4}}^{2} = C_{2},{S_{4}}^{3},{S_{4}}^{4} = E \right\}\) and \(\left\{ \overline{4},{\overline{4}}^{2} = 2,{\overline{4}}^{3},{\overline{4}}^{4} = 1 \right\}\) are identical because they yield the same four points. However, \(S_{4} = {\overline{4}}^{3} = {(\overline{4})}^{- 1}\) and \(\overline{4} = {S_{4}}^{3} = {S_{4}}^{- 1}\). Also, the figure displays the change in handedness of the comma when it is moved by an improper rotation.

As the example illustrates, the orientation of a symmetry operation, except the identity and inversion, is specified by the direction of its axis, which is perpendicular to the act of rotation or the reflection plane. To specify the orientation of any operation, a subscript may be added to the symbol (see figure): e.g., \(C_{4z} = 4_{z}\) is a 90° ccw rotation about the z-axis and \(\sigma_{y} = m_{y}\) is a reflection through the xz-plane. In the Schönflies notation, reflections are differentiated by their orientations with respect to a principal rotation axis and any perpendicular two-fold axis in the point group: \(\sigma_{h}\) is a reflection perpendicular to the principal rotation axis; \(\sigma_{v}\) is a mirror parallel to both the principal axis and a perpendicular two-fold axis; \(\sigma_{d}\) is a mirror parallel to the principal axis and bisecting two perpendicular two-fold axes. In the International notation, reflections perpendicular to a rotation axis are denoted \(/m\) (read “over m”); otherwise, the slash is omitted.

Figure 2.9: (Left side) Counterclockwise rotation by angle 2pi/n in plane perpendicular to the z-axis.(Right side) Orientation of reflection plane perpendicular to the y-axis.

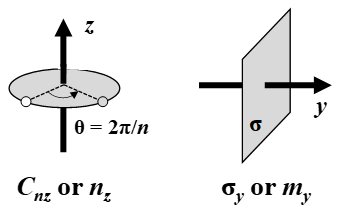
Lastly, the characteristics of the matrix representations or the geometrical evaluation of products \(S_{4}^{m}\) (\(m = 1, 2, 3, 4\)) in the example readily lead the following relationships for products of rotations:

• Proper rotation × Proper rotation = Proper rotation
• Proper rotation × Improper rotation = Improper rotation
• Improper rotation × Improper rotation = Proper rotation

These rules are important when enumerating the various 3-d point groups.