9.12: Lattice Energies and Solubility
- Page ID
- 189518
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
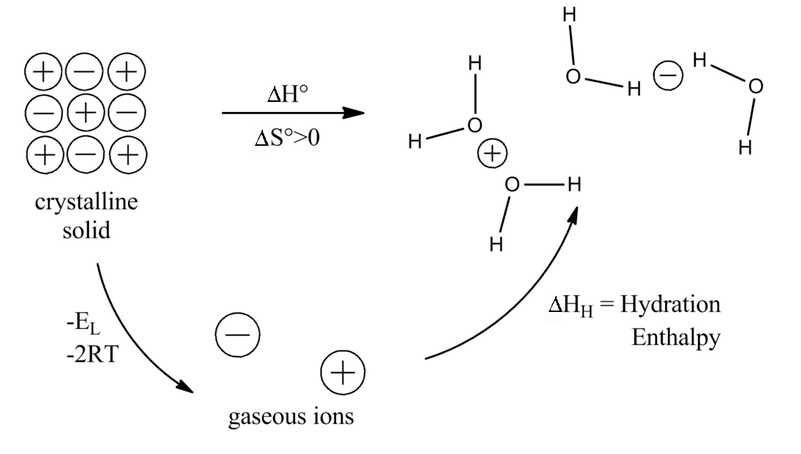
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lattice energies can also help predict compound solubilities. Let's consider a Born-Haber cycle for dissolving a salt in water. We can imagine this as the sum of two processes: (1) the vaporization of the salt to produce gaseous ions, characterized by the lattice enthalpy, and (2) the hydration of those ions to produce the solution. The enthalpy change for the overall process is the sum of those two steps. We know that the entropy change for dissolution of a solid is positive, so the solubility depends on the enthalpy change for the overall process.
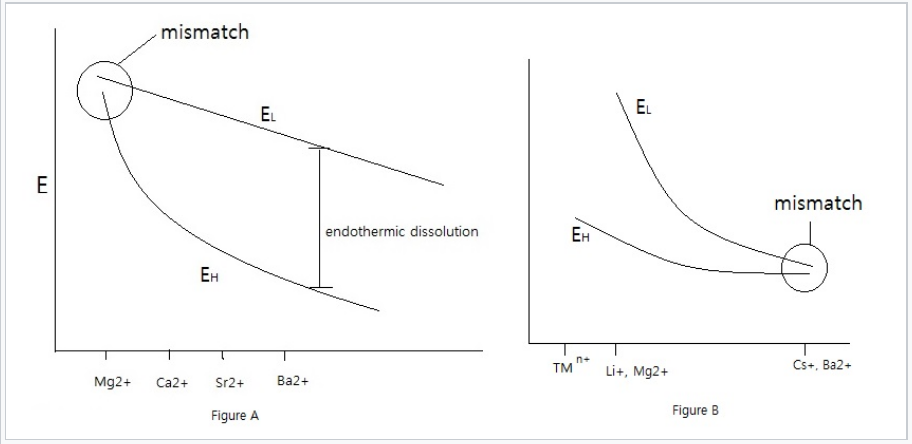
Here we need to consider the trends in both the lattice energy EL and the hydration energy EH. The lattice energy depends on the sum of the anion and cation radii (r+ + r-), whereas the hydration energy has separate anion and cation terms. Generally the solvation of small ions (typically cations) dominates the hydration energy because of the 1/r2 dependence.
\[E_{L} \alpha \frac{1}{r_{+}+ r_{-}}\]
\[E_{H} \alpha \frac{1}{r_{+}^{2}} + \frac{1}{r_{-}^{2}}\]
For salts that contain large anions, EL doesn't change much as r+ changes. That is because the anion dominates the r+ + r- term in the denominator of the formula for EL. On the other hand, EH changes substantially with r+, especially for small cations.
As a result, sulfate salts of small divalent cations, such as MgSO4 (epsom salts), are soluble, whereas the lower hydration energy of Ba2+ in BaSO4 makes that salt insoluble (Ksp = 10-10).
|
Left: EL diagram for sulfate salts. The large SO42- ion is size-mismatched to small cations such as Mg2+, which have large hydration energies, resulting soluble salts. With larger cations such as Ba2+, which have lower EH, the lattice energy exceeds the solvation enthalpy and the salts are insoluble.. Right: In the case of small anions such as F- and OH-, the lattice energy dominates with small cations such as transition metal ions (TMn+), Mg2+, and Li+. Anion-cation size mismatch occurs with larger cations, such as Cs+ and Ba2+, which make soluble fluoride salts. |
For small anions, EL is more sensitive to r+, whereas EH does not depend on r+ as strongly. For fluorides and hydroxides, LiF is slightly soluble whereas CsF is very soluble, and Mg(OH)2 is insoluble whereas Ba(OH)2 is very soluble.
Putting both trends together, we see that low solubility is most often encountered when the anion and cation match well in their sizes, especially when one or both are multiply charged.
|
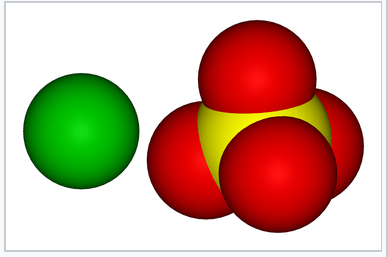
Space-filling models showing the van der Waals surfaces of Ba2+ and SO42-. The similarity in size of the two ions contributes to the low solubility of BaSO4 in water. |
Combining all our conclusions about solubility, we note the following trends:
1) Increasing size mismatch between the anion and cation leads to greater solubility, so CsF and LiI are the most soluble alkali halides.
2) Increasing covalency leads to lower solubility in the salts (due to larger EL. For example, AgF, AgCl, AgBr, and AgI exhibit progressively lower solubility because of increasing covalency.
\(\ce{AgF > AgCl > AgBr > AgI}\)
3) Increasing the charge on the anion lowers the solubility because the increase in EL is large relative to the increase in EH.
4) Small, polyvalent cations (having large EH) make soluble salts with large, univalent anions such as I-, NO3-, ClO4-, PF6-, and acetate.
Examples: Salts of transition metal and lanthanide ions
- Ln3+: Nitrate salts are soluble, but oxides and hydroxides are insoluble.
- Fe3+: Perchlorate is soluble, but sulfate is insoluble.
5) Multiple charged anions such as O2-, S2-, PO43-, and SO42- make insoluble salts with most M2+, M3+, and M4+ metals.