14.6: Reaction Directions (Empirical Explanation)
- Page ID
- 41618
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To predict in which direction a reaction will proceed.
- Describe the ways in which an equilibrium system can be stressed
- Predict the response of a stressed equilibrium using Le Chatelier’s principle
We previously saw that knowing the magnitude of the equilibrium constant under a given set of conditions allows chemists to predict the extent of a reaction. Often, however, chemists must decide whether a system has reached equilibrium or if the composition of the mixture will continue to change with time. In this section, we describe how to quantitatively analyze the composition of a reaction mixture to make this determination.
The Reaction Quotient
To determine whether a system has reached equilibrium, chemists use a quantity called the Reaction Quotient (\(Q\)). The expression for the Reaction Quotient has precisely the same form as the equilibrium constant expression from the Law of Mass Action, except that \(Q\) may be derived from a set of values measured at any time during the reaction of any mixture of the reactants and the products, regardless of whether the system is at equilibrium. Therefore, for the following general reaction:
the Reaction Quotient is defined as follows:
\[Q=\dfrac{[C]^c[D]^d}{[A]^a[B]^b} \label{Eq1}\]
To understand how information is obtained using a Reaction Quotient, consider the dissociation of dinitrogen tetroxide to nitrogen dioxide,
\[\ce{N2O4(g) \rightleftharpoons 2NO2(g)}. \label{Rx}\]
For this reaction, \(K = 4.65 \times 10^{−3}\) at 298 K. We can write \(Q\) for this reaction as follows:
The following table lists data from three experiments in which samples of the reaction mixture were obtained and analyzed at equivalent time intervals, and the corresponding values of \(Q\) were calculated for each. Each experiment begins with different proportions of product and reactant:
| Experiment | \([NO_2]\; (M)\) | \([N_2O_4]\; (M)\) | \(Q = \dfrac{[NO^2]^2}{[N^2O^4]}\) |
|---|---|---|---|
| 1 | 0 | 0.0400 | \(\dfrac{0^2}{0.0400}=0\) |
| 2 | 0.0600 | 0 | \(\dfrac{(0.0600)^2}{0}=\text{undefined}\) |
| 3 | 0.0200 | 0.0600 | \(\dfrac{(0.0200)^2}{0.0600}=6.67 \times 10^{−3}\) |
As these calculations demonstrate, \(Q\) can have any numerical value between 0 and infinity (undefined); that is, \(Q\) can be greater than, less than, or equal to K.
Comparing the magnitudes of \(Q\) and K enables us to determine whether a reaction mixture is already at equilibrium and, if it is not, predict how its composition will change with time to reach equilibrium (i.e., whether the reaction will proceed to the right or to the left as written). All you need to remember is that the composition of a system not at equilibrium will change in a way that makes \(Q\) approach K. If \(Q = K\), for example, then the system is already at equilibrium, and no further change in the composition of the system will occur unless the conditions are changed. If \(Q < K\), then the ratio of the concentrations of products to the concentrations of reactants is less than the ratio at equilibrium. Therefore, the reaction will proceed to the right as written, forming products at the expense of reactants. Conversely, if \(Q > K\), then the ratio of the concentrations of products to the concentrations of reactants is greater than at equilibrium, so the reaction will proceed to the left as written, forming reactants at the expense of products. These points are illustrated graphically in Figure \(\PageIndex{1}\).
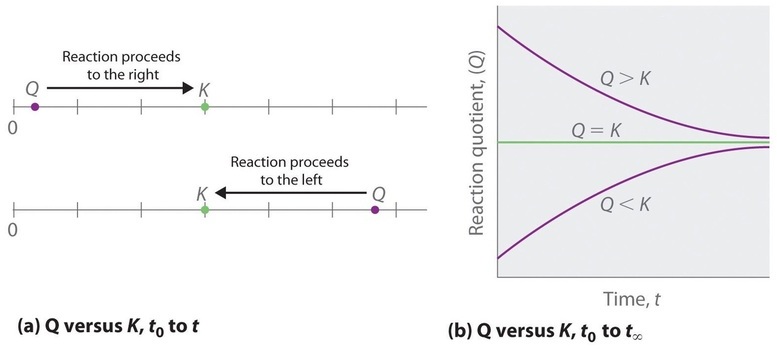
If \(Q < K\), the reaction will proceed to the right as written. If \(Q > K\), the reaction will proceed to the left as written. If \(Q = K\), then the system is at equilibrium.
At elevated temperatures, methane (\(CH_4\)) reacts with water to produce hydrogen and carbon monoxide in what is known as a steam-reforming reaction:
\[\ce{CH4(g) + H2O (g) \rightleftharpoons CO (g) + 3H2(g)} \nonumber \]
\(K = 2.4 \times 10^{−4}\) at 900 K. Huge amounts of hydrogen are produced from natural gas in this way and are then used for the industrial synthesis of ammonia. If \(1.2 × 10^{−2}\) mol of \(CH_4\), \(8.0 × 10^{−3}\) mol of \(H_2O\), \(1.6 \times 10^{−2}\) mol of \(CO\), and \(6.0 \times 10^{−3}\) mol of \(H_2\) are placed in a 2.0 L steel reactor and heated to 900 K, will the reaction be at equilibrium or will it proceed to the right to produce \(CO\) and \(H_2\) or to the left to form \(CH_4\) and \(H_2O\)?
Given: balanced chemical equation, \(K\), amounts of reactants and products, and volume
Asked for: direction of reaction
Strategy:
- Calculate the molar concentrations of the reactants and the products.
- Use Equation \(\ref{Eq1}\) to determine \(Q\). Compare \(Q\) and \(K\) to determine in which direction the reaction will proceed.
Solution:
A: We must first find the initial concentrations of the substances present. For example, we have \(1.2 \times 10^{−2} mol\) of \(CH_4\) in a 2.0 L container, so
\[\begin{align*} [CH_4]&=\dfrac{1.2\times 10^{−2} mol}{2.0\; L} \\[4pt] &=6.0 \times 10^{−3} M \end{align*}\]
We can calculate the other concentrations in a similar way:
- \([H_2O] = 4.0 \times 10^{−3} M\),
- \([CO] = 8.0 \times 10^{−3} M\), and
- \([H_2] = 3.0 \times 10^{−3} M\).
B: We now compute \(Q\) and compare it with \(K\):
\[\begin{align*} Q&=\dfrac{[CO][H_2]^3}{[CH_4][H_2O]} \\[4pt] &=\dfrac{(8.0 \times 10^{−3})(3.0 \times 10^{−3})^3}{(6.0\times 10^{−3})(4.0 \times 10^{−3})} \\[4pt] &=9.0 \times 10^{−6} \end{align*}\]
Because \(K = 2.4 × 10^{−4}\), we see that \(Q < K\). Thus the ratio of the concentrations of products to the concentrations of reactants is less than the ratio for an equilibrium mixture. The reaction will therefore proceed to the right as written, forming \(\ce{H2}\) and \(\ce{CO}\) at the expense of \(H_2O\) and \(CH_4\).
In the water–gas shift reaction introduced in Example \(\PageIndex{1}\), carbon monoxide produced by steam-reforming reaction of methane reacts with steam at elevated temperatures to produce more hydrogen:
\[\ce{ CO (g) + H2O (g) \rightleftharpoons CO2(g) +H2(g)} \nonumber\]
\(K = 0.64\) at 900 K. If 0.010 mol of both \(\ce{CO}\) and \(\ce{H_2O}\), 0.0080 mol of \(\ce{CO_2}\), and 0.012 mol of \(\ce{H_2}\) are injected into a 4.0 L reactor and heated to 900 K, will the reaction proceed to the left or to the right as written?
- Answer
-
\(Q = 0.96\) (Q > K), so the reaction will proceed to the left, and \(CO\) and \(H_2O\) will form.
Predicting the Direction of a Reaction with a Graph
By graphing a few equilibrium concentrations for a system at a given temperature and pressure, we can readily see the range of reactant and product concentrations that correspond to equilibrium conditions, for which \(Q = K\). Such a graph allows us to predict what will happen to a reaction when conditions change so that \(Q\) no longer equals \(K\), such as when a reactant concentration or a product concentration is increased or decreased.
Lead carbonate decomposes to lead oxide and carbon dioxide according to the following equation:
\[\ce{PbCO3(s) \rightleftharpoons PbO(s) + CO2(g)} \label{Eq3}\]
Because \(PbCO_3\) and \(PbO\) are solids, the equilibrium constant is simply \(K = [CO_2]\). At a given temperature, therefore, any system that contains solid \(PbCO_3\) and solid \(PbO\) will have exactly the same concentration of \(CO_2\) at equilibrium, regardless of the ratio or the amounts of the solids present. This situation is represented in Figure \(\PageIndex{2}\), which shows a plot of \([CO_2]\) versus the amount of \(PbCO_3\) added. Initially, the added \(PbCO_3\) decomposes completely to \(CO_2\) because the amount of \(PbCO_3\) is not sufficient to give a \(CO_2\) concentration equal to \(K\). Thus the left portion of the graph represents a system that is not at equilibrium because it contains only CO2(g) and PbO(s). In contrast, when just enough \(PbCO_3\) has been added to give \([CO_2] = K\), the system has reached equilibrium, and adding more \(PbCO_3\) has no effect on the \(CO_2\) concentration: the graph is a horizontal line. Thus any \(CO_2\) concentration that is not on the horizontal line represents a nonequilibrium state, and the system will adjust its composition to achieve equilibrium, provided enough \(PbCO_3\) and \(PbO\) are present. For example, the point labeled A in Figure \(\PageIndex{2}\) lies above the horizontal line, so it corresponds to a \([CO_2]\) that is greater than the equilibrium concentration of \(CO_2\) (Q > K). To reach equilibrium, the system must decrease \([CO_2]\), which it can do only by reacting \(CO_2\) with solid \(PbO\) to form solid \(PbCO_3\). Thus the reaction in Equation \(\ref{Eq3}\) will proceed to the left as written, until \([CO_2] = K\). Conversely, the point labeled B in Figure \(\PageIndex{2}\) lies below the horizontal line, so it corresponds to a \([CO_2]\) that is less than the equilibrium concentration of \(CO_2\) (Q < K). To reach equilibrium, the system must increase \([CO_2]\), which it can do only by decomposing solid \(PbCO_3\) to form \(CO_2\) and solid \(PbO\). The reaction in Equation \(\ref{Eq3}\) will therefore proceed to the right as written, until \([CO_2] = K\).
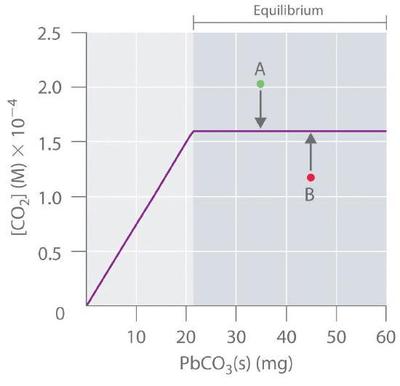
In contrast, the reduction of cadmium oxide by hydrogen gives metallic cadmium and water vapor:
\[\ce{CdO (s) + H2(g) \rightleftharpoons Cd (s) + H2O(g)} \label{Eq4}\]
and the equilibrium constant K is \([H_2O]/[H_2]\). If \([H_2O]\) is doubled at equilibrium, then [H2] must also be doubled for the system to remain at equilibrium. A plot of \([H_2O]\) versus \([H_2]\) at equilibrium is a straight line with a slope of K (Figure \(\PageIndex{3}\)). Again, only those pairs of concentrations of \(H_2O\) and \(H_2\) that lie on the line correspond to equilibrium states. Any point representing a pair of concentrations that does not lie on the line corresponds to a nonequilibrium state. In such cases, the reaction in Equation \(\ref{Eq4}\) will proceed in whichever direction causes the composition of the system to move toward the equilibrium line. For example, point A in Figure \(\PageIndex{3}\) lies below the line, indicating that the \([H_2O]/[H_2]\) ratio is less than the ratio of an equilibrium mixture (Q < K). Thus the reaction in Equation \(\ref{Eq4}\) will proceed to the right as written, consuming \(H_2\) and producing \(H_2O\), which causes the concentration ratio to move up and to the left toward the equilibrium line. Conversely, point B in Figure \(\PageIndex{3}\) lies above the line, indicating that the \([H_2O]/[H_2]\) ratio is greater than the ratio of an equilibrium mixture (Q > K). Thus the reaction in Equation \(\ref{Eq4}\) will proceed to the left as written, consuming \(H_2O\) and producing \(H_2\), which causes the concentration ratio to move down and to the right toward the equilibrium line.
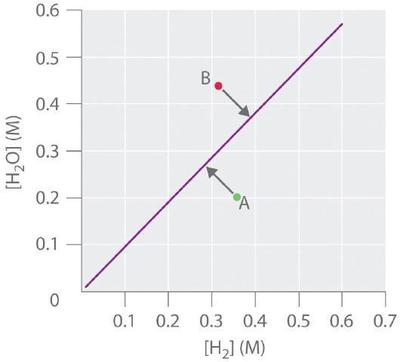
In another example, solid ammonium iodide dissociates to gaseous ammonia and hydrogen iodide at elevated temperatures:
\[ NH_4I_{(s)} \rightleftharpoons NH_{3(g)}+HI_{(g)} \label{Eq5}\]
For this system, \(K\) is equal to the product of the concentrations of the two products: \([NH_3][HI]\). If we double the concentration of NH3, the concentration of HI must decrease by approximately a factor of 2 to maintain equilibrium, as shown in Figure \(\PageIndex{4}\). As a result, for a given concentration of either \(HI\) or \(NH_3\), only a single equilibrium composition that contains equal concentrations of both \(NH_3\) and HI is possible, for which \([NH_3] = [HI] = K^{1/2}\). Any point that lies below and to the left of the equilibrium curve (such as point A in Figure \(\PageIndex{4}\)) corresponds to \(Q < K\), and the reaction in Equation \(\ref{Eq5}\) will therefore proceed to the right as written, causing the composition of the system to move toward the equilibrium line. Conversely, any point that lies above and to the right of the equilibrium curve (such as point B in Figure \(\PageIndex{4}\)) corresponds to \(Q > K\), and the reaction in Equation \(\ref{Eq5}\) will therefore proceed to the left as written, again causing the composition of the system to move toward the equilibrium line. By graphing equilibrium concentrations for a given system at a given temperature and pressure, we can predict the direction of reaction of that mixture when the system is not at equilibrium.
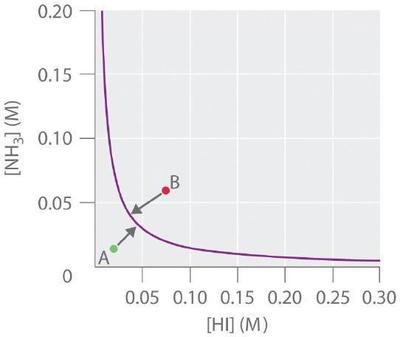
Effect of Change in Pressure on Equilibrium
Sometimes we can change the position of equilibrium by changing the pressure of a system. However, changes in pressure have a measurable effect only in systems in which gases are involved, and then only when the chemical reaction produces a change in the total number of gas molecules in the system. An easy way to recognize such a system is to look for different numbers of moles of gas on the reactant and product sides of the equilibrium. While evaluating pressure (as well as related factors like volume), it is important to remember that equilibrium constants are defined with regard to concentration (for \(K_c\)) or partial pressure (for \(K_p\)). Some changes to total pressure, like adding an inert gas that is not part of the equilibrium, will change the total pressure but not the partial pressures of the gases in the equilibrium constant expression. Thus, addition of a gas not involved in the equilibrium will not perturb the equilibrium.
As we increase the pressure of a gaseous system at equilibrium, either by decreasing the volume of the system or by adding more of one of the components of the equilibrium mixture, we introduce a stress by increasing the partial pressures of one or more of the components. In accordance with Le Chatelier's principle, a shift in the equilibrium that reduces the total number of molecules per unit of volume will be favored because this relieves the stress. The reverse reaction would be favored by a decrease in pressure.
Consider what happens when we increase the pressure on a system in which \(\ce{NO}\), \(\ce{O_2}\), and \(\ce{NO_2}\) are at equilibrium:
\[\ce{2NO}_{(g)}+\ce{O}_{2(g)} \rightleftharpoons \ce{2NO}_{2(g)} \label{Eq8}\]
The formation of additional amounts of \(\ce{NO2}\) decreases the total number of molecules in the system because each time two molecules of \(\ce{NO_2}\) form, a total of three molecules of \(\ce{NO}\) and \(\ce{O_2}\) are consumed. This reduces the total pressure exerted by the system and reduces, but does not completely relieve, the stress of the increased pressure. On the other hand, a decrease in the pressure on the system favors decomposition of \(\ce{NO_2}\) into \(\ce{NO}\) and \(\ce{O_2}\), which tends to restore the pressure.
Now consider this reaction:
\[\ce{N2}(g)+\ce{O2}(g)\rightleftharpoons\ce{2NO}(g) \label{Eq9}\]
Because there is no change in the total number of molecules in the system during reaction, a change in pressure does not favor either formation or decomposition of gaseous nitrogen monoxide.
Effect of Change in Temperature on Equilibrium
Changing concentration or pressure perturbs an equilibrium because the Reaction Quotient is shifted away from the equilibrium value. Changing the temperature of a system at equilibrium has a different effect: A change in temperature actually changes the value of the equilibrium constant. However, we can qualitatively predict the effect of the temperature change by treating it as a stress on the system and applying Le Chatelier's principle.
When hydrogen reacts with gaseous iodine, heat is evolved.
\[\ce{H2(g) + I2(g) \rightleftharpoons 2HI (g)} \;\;\ ΔH=\mathrm{−9.4\;kJ\;(exothermic)} \label{Eq10}\]
Because this reaction is exothermic, we can write it with heat as a product.
\[\ce{H2(g) + I2(g) \rightleftharpoons 2HI (g) + heat} \label{Eq11}\]
Increasing the temperature of the reaction increases the internal energy of the system. Thus, increasing the temperature has the effect of increasing the amount of one of the products of this reaction. The reaction shifts to the left to relieve the stress, and there is an increase in the concentration of \(\ce{H2}\) and \(\ce{I2}\) and a reduction in the concentration of \(\ce{HI}\). Lowering the temperature of this system reduces the amount of energy present, favors the production of heat, and favors the formation of hydrogen iodide.
When we change the temperature of a system at equilibrium, the equilibrium constant for the reaction changes. Lowering the temperature in the \(\ce{HI}\) system increases the equilibrium constant: At the new equilibrium the concentration of \(\ce{HI}\) has increased and the concentrations of \(\ce{H2}\) and \(\ce{I2}\) decreased. Raising the temperature decreases the value of the equilibrium constant, from 67.5 at 357 °C to 50.0 at 400 °C.
Temperature affects the equilibrium between \(\ce{NO_2}\) and \(\ce{N_2O_4}\) in this reaction
\[\ce{N_2O}_{4(g)} \rightleftharpoons \ce{2NO}_{2(g)}\;\;\; ΔH=\mathrm{57.20\; kJ} \label{Eq12}\]
The positive \(ΔH\) value tells us that the reaction is endothermic and could be written
\[\ce{heat}+\ce{N_2O}_{4(g)} \rightleftharpoons \ce{2NO}_{2(g)} \label{Eq13}\]
At higher temperatures, the gas mixture has a deep brown color, indicative of a significant amount of brown \(\ce{NO_2}\) molecules. If, however, we put a stress on the system by cooling the mixture (withdrawing energy), the equilibrium shifts to the left to supply some of the energy lost by cooling. The concentration of colorless \(\ce{N_2O_4}\) increases, and the concentration of brown \(\ce{NO_2}\) decreases, causing the brown color to fade.
It is not uncommon that textbooks and instructors to consider heat as a independent "species" in a reaction. While this is rigorously incorrect because one cannot "add or remove heat" to a reaction as with species, it serves as a convenient mechanism to predict the shift of reactions with changing temperature. For example, if heat is a "reactant" (\(\Delta{H} > 0 \)), then the reaction favors the formation of products at elevated temperature. Similarly, if heat is a "product" (\(\Delta{H} < 0 \)), then the reaction favors the formation of reactants. A more accurate, and hence preferred, description is discussed below.
The commercial production of hydrogen is carried out by treating natural gas with steam at high temperatures and in the presence of a catalyst (“steam reforming of methane”):
\[\ce{CH_4 + H_2O <=> CH_3OH + H_2} \nonumber\]
Given the following boiling points: CH4 (methane) = –161°C, H2O = 100°C, CH3OH = 65°, H2 = –253°C, predict the effects of an increase in the total pressure on this equilibrium at 50°, 75° and 120°C.
Solution
To identify the influence of changing pressure on the three reaction conditions, we need to identify the correct reaction including the phase of each reactant and product. Calculate the change in the moles of gas for each process:
|
Temperature |
|---|
What will happen to the equilibrium when the volume of the system is decreased?
\[\ce{2SO2 (g) + O2 (g) \rightleftharpoons 2SO3 (g)} \nonumber\]
- Answer
-
Decreasing the volume leads to an increase in pressure which will cause the equilibrium to shift towards the side with fewer moles. In this reaciton, there are three moles on the reactant side and two moles on the product side, so the new equilibrium will shift towards the products (to the right).
Summary
The Reaction Quotient (Q) is used to determine whether a system is at equilibrium and if it is not, to predict the direction of reaction. Reaction Quotient: \[Q =\dfrac{[C]^c[D]^d}{[A]^a[B]^b} \nonumber\] The Reaction Quotient (\(Q\) or \(Q_p\)) has the same form as the equilibrium constant expression, but it is derived from concentrations obtained at any time. When a reaction system is at equilibrium, \(Q = K\). Graphs derived by plotting a few equilibrium concentrations for a system at a given temperature and pressure can be used to predict the direction in which a reaction will proceed. Points that do not lie on the line or curve represent nonequilibrium states, and the system will adjust, if it can, to achieve equilibrium.
Systems at equilibrium can be disturbed by changes to temperature, concentration, and, in some cases, volume and pressure; volume and pressure changes will disturb equilibrium if the number of moles of gas is different on the reactant and product sides of the reaction. The system's response to these disturbances is described by Le Chatelier's principle: The system will respond in a way that counteracts the disturbance. Not all changes to the system result in a disturbance of the equilibrium. Adding a catalyst affects the rates of the reactions but does not alter the equilibrium, and changing pressure or volume will not significantly disturb systems with no gases or with equal numbers of moles of gas on the reactant and product side.
| Disturbance | Observed Change as Equilibrium is Restored | Direction of Shift | Effect on K |
|---|---|---|---|
| reactant added | added reactant is partially consumed | toward products | none |
| product added | added product is partially consumed | toward reactants | none |
| decrease in volume/increase in gas pressure | pressure decreases | toward side with fewer moles of gas | none |
| increase in volume/decrease in gas pressure | pressure increases | toward side with more moles of gas | none |
| temperature increase | heat is absorbed | toward products for endothermic, toward reactants for exothermic | changes |
| temperature decrease | heat is given off | toward reactants for endothermic, toward products for exothermic | changes |
Footnotes
- 1 Herrlich, P. “The Responsibility of the Scientist: What Can History Teach Us About How Scientists Should Handle Research That Has the Potential to Create Harm?” EMBO Reports 14 (2013): 759–764.
Glossary
- Le Chatelier's principle
- when a chemical system at equilibrium is disturbed, it returns to equilibrium by counteracting the disturbance
- position of equilibrium
- concentrations or partial pressures of components of a reaction at equilibrium (commonly used to describe conditions before a disturbance)
- stress
- change to a reaction's conditions that may cause a shift in the equilibrium
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

