24.7: Color and the Colors of Complexes
- Page ID
- 24356
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
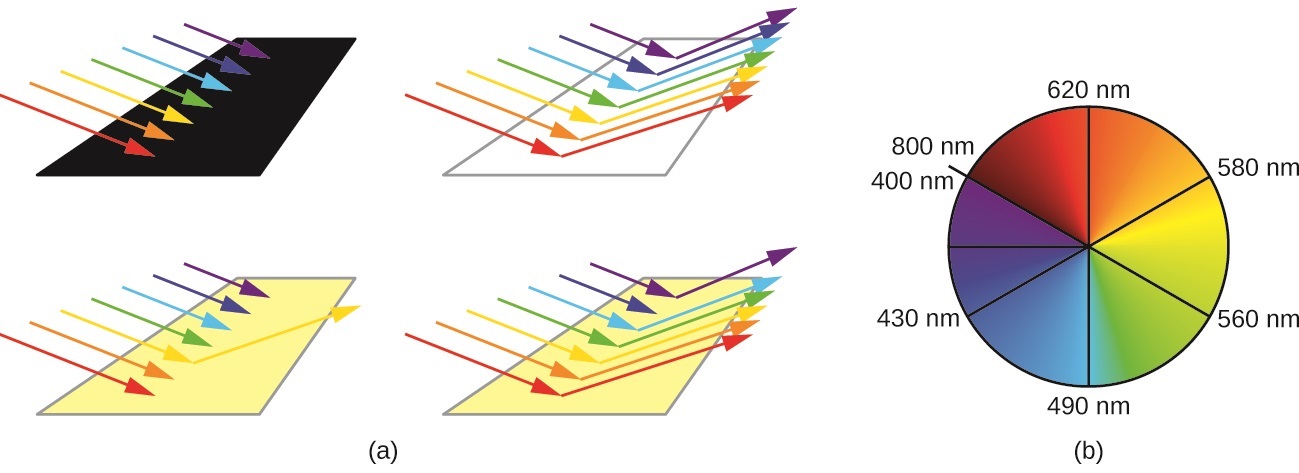
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The human eye perceives a mixture of all the colors, in the proportions present in sunlight, as white light. Complementary colors, those located across from each other on a color wheel, are also used in color vision. The eye perceives a mixture of two complementary colors, in the proper proportions, as white light. Likewise, when a color is missing from white light, the eye sees its complement. For example, when red photons are absorbed from white light, the eyes see the color green. When violet photons are removed from white light, the eyes see lemon yellow (Figure \(\PageIndex{1}\)).
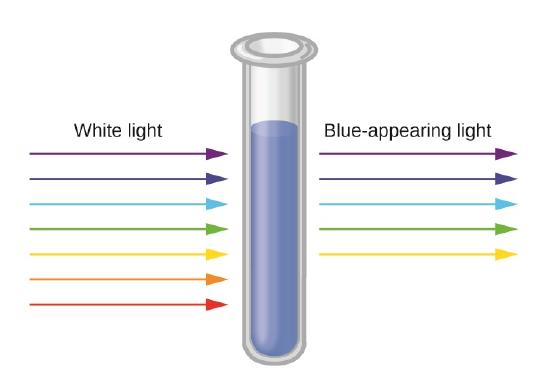
The blue color of the \(\ce{[Cu(NH3)4]^{2+}}\) ion results because this ion absorbs orange and red light, leaving the complementary colors of blue and green (Figure \(\PageIndex{2}\)). If white light (ordinary sunlight, for example) passes through \(\ce{[Cu(NH3)4]SO4}\) solution, some wavelengths in the light are absorbed by the solution. The \(\ce{[Cu(NH3)4]^{2+}}\) ions in solution absorb light in the red region of the spectrum. The light which passes through the solution and out the other side will have all the colors in it except for the red. We see this mixture of wavelengths as pale blue (cyan). The diagram gives an impression of what happens if you pass white light through a \(\ce{[Cu(NH_3)_4]SO_4}\) solution.
Working out what color you will see is not easy if you try to do it by imagining "mixing up" the remaining colors. You would not have thought that all the other colors apart from some red would look cyan, for example. Sometimes what you actually see is quite unexpected. Mixing different wavelengths of light doesn't give you the same result as mixing paints or other pigments. You can, however, sometimes get some estimate of the color you would see using the idea of complementary colors.
Recall that the color we observe when we look at an object or a compound is due to light that is transmitted or reflected, not light that is absorbed, and that reflected or transmitted light is complementary in color to the light that is absorbed. Thus a green compound absorbs light in the red portion of the visible spectrum and vice versa, as indicated by the complementary color wheel.

The striking colors exhibited by transition-metal complexes are caused by excitation of an electron from a lower-energy d orbital to a higher-energy d orbital, which is called a d–d transition (Figure \(\PageIndex{4}\)). For a photon to effect such a transition, its energy must be equal to the difference in energy between the two d orbitals, which depends on the magnitude of Δo.
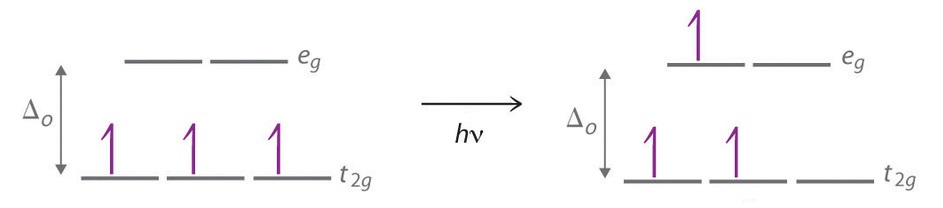
The octahedral complex [Ti(H2O)6]3+ has a single d electron. To excite this electron from the ground state t2g orbital to the eg orbital, this complex absorbs light from 450 to 600 nm. The maximum absorbance corresponds to Δo and occurs at 499 nm. Calculate the value of Δo in Joules and predict what color the solution will appear.
Solution
We can convert wavelength to frequency:
\[\begin{align*} \nu &=\dfrac{c}{λ} \\[4pt] &= \dfrac{3.00 \times 10^8 \, m/s} { (499\, \cancel{nm}) \times \left( \dfrac{1 \,m}{10^9\, \cancel{ nm}} \right)} \\[4pt] &=6.01 \times 10^{14} s^{-1} =6.01 \times 10^{14} \,Hz \end{align*}\]
And then using Planck's equation that related the frequency of light to energy
\[E=h \nu \nonumber\]
so
\[\begin{align*} E &= (6.63 \times 10^{−34} \textrm{J⋅s} ) \times (6.01 \times 10^{14} \,Hz) \\[4pt] &=3.99 \times 10^{−19} \,J \end{align*}\]
Because the complex absorbs 600 nm (orange) through 450 (blue), the indigo, violet, and red wavelengths will be transmitted, and the complex will appear purple.
Note: This is the energy for one transition (i.e., in one complex). If you want to calculate the energy in J/mol, then you have to multiply this by Avogadro's number (\(N_A\)).
A complex that appears green, absorbs photons of what wavelengths?
- Answer
- red, 620–800 nm
Color Depends on Oxidation State
Small changes in the relative energies of the orbitals that electrons are transitioning between can lead to drastic shifts in the color of light absorbed. Therefore, the colors of coordination compounds depend on many factors. As shown in Figure \(\PageIndex{4}\), different aqueous metal ions can have different colors. In addition, different oxidation states of one metal can produce different colors, as shown for the vanadium complexes in the link below.
Watch this video of the reduction of vanadium complexes to observe the colorful effect of changing oxidation states.
Color Depends on Ligand Field
The specific ligands coordinated to the metal center also influence the color of coordination complexes. Because the energy of a photon of light is inversely proportional to its wavelength, the color of a complex depends on the magnitude of Δo, which depends on the structure of the complex. For example, the complex [Cr(NH3)6]3+ has strong-field ligands and a relatively large Δo. Consequently, it absorbs relatively high-energy photons, corresponding to blue-violet light, which gives it a yellow color. A related complex with weak-field ligands, the [Cr(H2O)6]3+ ion, absorbs lower-energy photons corresponding to the yellow-green portion of the visible spectrum, giving it a deep violet color. For example, the iron(II) complex [Fe(H2O)6]SO4 appears blue-green because the high-spin complex absorbs photons in the red wavelengths (Figure \(\PageIndex{5}\)). In contrast, the low-spin iron(II) complex K4[Fe(CN)6] appears pale yellow because it absorbs higher-energy violet photons.

In general, strong-field ligands cause a large split in the energies of d orbitals of the central metal atom (large Δoct). Transition metal coordination compounds with these ligands are yellow, orange, or red because they absorb higher-energy violet or blue light. On the other hand, coordination compounds of transition metals with weak-field ligands are often blue-green, blue, or indigo because they absorb lower-energy yellow, orange, or red light.
Strong-field ligands cause a large split in the energies of d orbitals of the central metal atom and transition metal coordination compounds with these ligands are typically yellow, orange, or red because they absorb higher-energy violet or blue light. Coordination compounds of transition metals with weak-field ligands are often blue-green, blue, or indigo because they absorb lower-energy yellow, orange, or red light.
Identify the color (either blue, green, yellow, or orange) for the following complex ions formed with \(Co^{3+}\):
- \([Co(CN)_6]_3^{-2} \)
- \([Co(NH_3)_6]_3^{3+}\)
- \([CoF_6]_3^{-4} \)
- \([Co(H_2O)_6]^{3+} \)
Solution
Each of these complex ions has the same metal with the same oxidation state, so the ligand field is the relevant factors. Each of the complex ions also has an octahedral ligand field, so we only need to compare the strength of the ligands in determining \(\Delta_o\), which is determined by the spectrochemical series.
The ligands for each complex ions are: (a) \(CN^-\), (b) \(NH_3\), (c) \(F^-\) and (d) \(H_2O\), which are ranked in increasing \(\Delta _o\) magnitude:
\[ F^- < H_2O < NH_3 < CN^- \label{eq0}\]
The relationship between the \(\Delta_o\) and the energy of the photons are absorbed in the d-d transition of \(\ce{Co^{3+}}\) is given by equating Planck's equation to the crystal field splitting parameter:
\[E= h \nu= \dfrac{hc}{\lambda} = \Delta_o \label{eq1}\]
Now, we need to get a relative correlation between observed color (to the eye) and the wavelength of the light that is absorbed. From the complementary color wheel in Figure \(\PageIndex{1}\) we get the following relationships (arranged from highest energy absorbed to lowest):
- 400-nm Violet light absorbed → Green-yellow observed
- 430-nm Blue light absorbed → Orange observed
- 450-nm Blue light absorbed → Yellow observed
- 490-nm Blue-green light absorbed → Red observed
- 570-nm Yellow-green light absorbed → Violet observed
- 580-nm Yellow light absorbed → Dark blue observed
- 600-nm Orange light absorbed → Blue observed
- 650-nm Red light absorbed → Green observed
Of the four possible colors given in the problem (blue, green, yellow, and orange), the corresponding colors that are absorbed are (600 nm, 650 nm, 450 nm, and 430, respectively). From Equation \(\ref{eq1}\), the smaller \(\lambda\) of absorbed light corresponds to the higher energy photons, so we would correlate the four wavelengths of absorbing photons in terms of increasing energy to observed color:
\[ \underbrace{650 \,nm }_{green} < \underbrace{600 \,nm}_{blue} < \underbrace{450 \, nm}_{yellow} < \underbrace{430 \, nm}_{orange} \label{eq3}\]
Now, just correlate the ranking in Equation \(\ref{eq3}\) to the ranking in Equation \(\ref{eq0}\):
\[ \underbrace{F^- }_{green} < \underbrace{ H_2O}_{blue} < \underbrace{NH_3}_{yellow} < \underbrace{CN^-}_{orange} \nonumber\]
and more specifically in terms of the original question
\[ \underbrace{[CoF_6]_3^{-4} }_{green} < \underbrace{ [Co(H_2O)_6]^{3+}}_{blue} < \underbrace{[Co(NH_3)_6]_3^{3+}}_{yellow} < \underbrace{[Co(CN)_6]_3^{-2}}_{orange} \nonumber\]
If a complex ion \([M(NH_3)_6]^{2+}\) is red in solution, which of the following ligands, after a ligand exchange reaction to substitute for the ammine ligands, may shift the solution to be orange? More than one answer is possible.
\(Cl^-\), \(CN^-\), \(CO\), \(F^-\) \(H_2O\), \(I^-\), \(en\), \(NO_2^-\), \(OH^-\), \(SCN^-\)
- Answer
- Shifting from red to orange is an increase in \(\Delta_o\), so those ligands that are stronger field ligands than \(NH_3\) in the list (deterimined via the spectrochemical series) are \(CN^-\), \(CO\), \(en\), and \(NO_2^-\).
A coordination compound of the Cu+ ion has a d10 configuration, and all the eg orbitals are filled. To excite an electron to a higher level, such as the 4p orbital, photons of very high energy are necessary. This energy corresponds to very short wavelengths in the ultraviolet region of the spectrum. No visible light is absorbed, so the eye sees no change, and the compound appears white or colorless. A solution containing [Cu(CN)2]−, for example, is colorless. On the other hand, octahedral Cu2+ complexes have a vacancy in the eg orbitals, and electrons can be excited to this level. The wavelength (energy) of the light absorbed corresponds to the visible part of the spectrum, and Cu2+ complexes are almost always colored—blue, blue-green violet, or yellow (Figure \(\PageIndex{6}\)). Although CFT successfully describes many properties of coordination complexes, molecular orbital explanations (beyond the introductory scope provided here) are required to understand fully the behavior of coordination complexes.

A ruby is a pink to blood-red colored gemstone that consist of trace amounts of chromium in the mineral corundum \(Al_2O_3\). In contrast, emeralds are colored green by trace amounts of chromium within a Be3Al2Si6O18 matrix. We can now understand why emeralds and rubies have such different colors, even though both contain Cr3+ in an octahedral environment provided by six oxide ions. Although the chemical identity of the six ligands is the same in both cases, the Cr–O distances are different because the compositions of the host lattices are different (Al2O3 in rubies and Be3Al2Si6O18 in emeralds). In ruby, the Cr–O distances are relatively short because of the constraints of the host lattice, which increases the d orbital–ligand interactions and makes Δo relatively large. Consequently, rubies absorb green light and the transmitted or reflected light is red, which gives the gem its characteristic color. In emerald, the Cr–O distances are longer due to relatively large [Si6O18]12− silicate rings; this results in decreased d orbital–ligand interactions and a smaller Δo. Consequently, emeralds absorb light of a longer wavelength (red), which gives the gem its characteristic green color. It is clear that the environment of the transition-metal ion, which is determined by the host lattice, dramatically affects the spectroscopic properties of a metal ion.

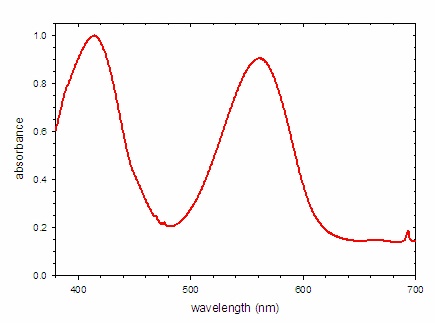
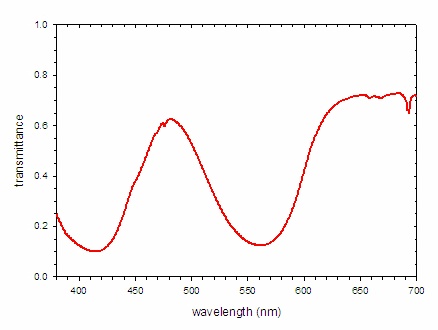
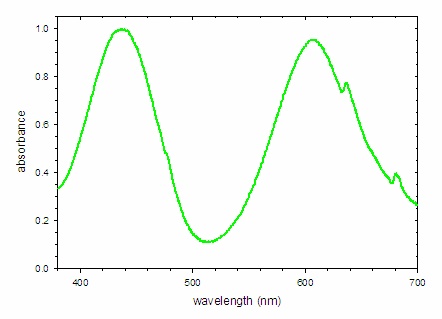
The absorbance spectrum of a ruby is shown Figure \(\PageIndex{7; left}\). The number and positions of the peaks in the spectrum is determined by the electronic structure of the compound, which in this case depends upon the identity of the metal and the identities, number, and geometry of the surrounding ions. Crystal field theory may be used to predict the electronic structure and thus the absorbance spectrum. If white light is shown on the gem, the absorbance spectrum indicates which wavelengths of light are removed. In this case, there are strong bands centered at 414 and 561 nm. These wavelengths correspond with blue and yellow-green light, respectively. For the most part, these colors are not present in the light reaching ones eyes. An alternative way to express this concept is to recognize that the spectrum of light reaching the eye is the product of the spectrum of the incident light (white light) and the transmittance spectrum. For this ruby, the transmittance spectrum has a peak at 481 nm and a broad plateau past 620 nm. (Note that there is significant attenuation of the light across the entire spectrum.) Thus only light with wavelengths near 481 nm (cyan) and greater than 620 nm (red) reach the eye.
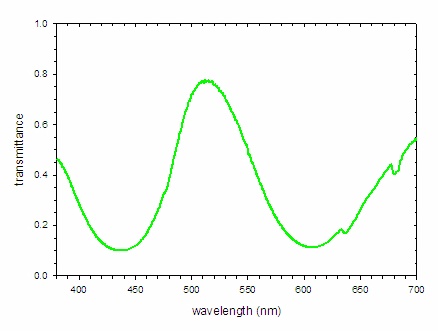
A similar analysis of the spectrum of an emerald is possible. The absorbance spectrum (Figure \(\PageIndex{8; left}\)) shows strong bands at 438 and 606 nm, which remove blue and orange light, respectively. The light that is not absorbed is shown by the transmittance spectrum, which indicates the dominant band of light reaching the eye is centered at 512 nm (green light) with smaller contributions from the far blue and red portions of the spectrum. This combination of wavelengths produces a deep green color.
Summary
When atoms or molecules absorb light at the proper frequency, their electrons are excited to higher-energy orbitals. For many main group atoms and molecules, the absorbed photons are in the ultraviolet range of the electromagnetic spectrum, which cannot be detected by the human eye. For coordination compounds, the energy difference between the d orbitals often allows photons in the visible range to be absorbed.
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).


