24.6: Magnetic Properties of Coordination Compounds and Crystal Field Theory
- Page ID
- 24355
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The magnetic properties of a compound can be determined from its electron configuration and the size of its atoms. Because magnetism is generated by electronic spin, the number of unpaired electrons in a specific compound indicates how magnetic the compound is. In this section, the magnetism of the d-block elements (or transition metals) are evaluated. These compounds tend to have a large number of unpaired electrons.
Introduction
An interesting characteristic of transition metals is their ability to form magnets. Metal complexes that have unpaired electrons are magnetic. Since the last electrons reside in the d orbitals, this magnetism must be due to having unpaired d electrons. The spin of a single electron is denoted by the quantum number \(m_s\) as +(1/2) or –(1/2). This spin is negated when the electron is paired with another, but creates a weak magnetic field when the electron is unpaired. More unpaired electrons increase the paramagnetic effects. The electron configuration of a transition metal (d-block) changes in a coordination compound; this is due to the repulsive forces between electrons in the ligands and electrons in the compound. Depending on the strength of the ligand, the compound may be paramagnetic or diamagnetic.
Bulk Magnetism: Ferromagnetism
Ferromagnetism is the basic mechanism by which certain materials (such as iron) form permanent magnets. This means the compound shows permanent magnetic properties rather than exhibiting them only in the presence of a magnetic field (Figure \(\PageIndex{1}\)). In a ferromagnetic element, electrons of atoms are grouped into domains in which each domain has the same charge. In the presence of a magnetic field, these domains line up so that charges are parallel throughout the entire compound. Whether a compound can be ferromagnetic or not depends on its number of unpaired electrons and on its atomic size.
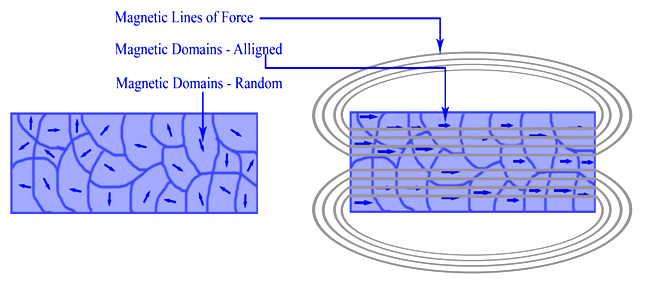
Ferromagnetism, the permanent magnetism associated with nickel, cobalt, and iron, is a common occurrence in everyday life. Examples of the knowledge and application of ferromagnetism include Aristotle's discussion in 625 BC, the use of the compass in 1187, and the modern-day refrigerator. Einstein declared that electricity and magnetism are inextricably linked in his theory of special relativity.
Magnetic Moments of Molecules and Ions
Experimental evidence of magnetic measurements supports the theory of high- and low-spin complexes. Remember that molecules such as O2 that contain unpaired electrons are paramagnetic. Paramagnetic substances are attracted to magnetic fields. Many transition metal complexes have unpaired electrons and hence are paramagnetic. Molecules such as N2 and ions such as Na+ and [Fe(CN)6]4− that contain no unpaired electrons are diamagnetic. Diamagnetic substances have a slight tendency to be repelled by magnetic fields.
When an electron in an atom or ion is unpaired, the magnetic moment due to its spin makes the entire atom or ion paramagnetic. The size of the magnetic moment of a system containing unpaired electrons is related directly to the number of such electrons: the greater the number of unpaired electrons, the larger the magnetic moment. Therefore, the observed magnetic moment is used to determine the number of unpaired electrons present. The measured magnetic moment of low-spin d6 [Fe(CN)6]4− confirms that iron is diamagnetic, whereas high-spin d6 [Fe(H2O)6]2+ has four unpaired electrons with a magnetic moment that confirms this arrangement.
Hunds' Rule states that electrons fill all available orbitals with single electrons before pairing up, while maintaining parallel spins (paired electrons have opposing spins). For a set of five degenerate d-orbitals in an uncomplexed metal atom, electrons fill all orbitals before pairing to conserve pairing energy. With the addition of ligands, the situation is more complicated. The splitting energy between the d-orbitals increases the energy required to place single electrons into the higher-energy orbitals. Once the lower-energy orbitals have been half-filled (one electron per orbital), an electron can either be placed in a higher-energy orbital or paired with an electron in a lower-energy orbital. The strength of the ligands determine which option is chosen. If the splitting energy is greater than the pairing energy, the electrons will pair up; if the pairing energy is greater, unpaired electrons will occupy higher energy orbitals. In other words, with a strong-field ligand, low-spin complexes are usually formed; with a weak-field ligand, a high-spin complex is formed.
Low-spin complexes contain more paired electrons because the splitting energy is larger than the pairing energy. These complexes, such as [Fe(CN)6]3-, are more often diamagnetic or weakly paramagnetic. Likewise, high-spin complexes usually contain more unpaired electrons because the pairing energy is larger than the splitting energy. With more unpaired electrons, high-spin complexes are often paramagnetic. The unpaired electrons in paramagnetic compounds create tiny magnetic fields, similar to the domains in ferromagnetic materials. The strength of the paramagnetism of a coordination complex increases with the number of unpaired electrons; a higher-spin complex is more paramagnetic. The occurrence and relative strength of paramagnetism can be predicted by determining whether the compound is coordinated to a weak field ligand or a strong field ligand.
Which ligand generates a stronger magnetic complex ion when bound to \(Fe^{+2}\): EDTA or \(CN^-\)?
Solution

Since \([Fe(EDTA)_3^{-2}]\) has more unpaired electrons than \([FeCN_6^{-3}]\), it is more paramagnetic.
\(ZnI_4\) have eight valence electrons. If it is found to be diamagnetic, then does it occupy a tetrahedral or square plan geometry?
Solution
The splitting pattern for the two geometries differ and hence the electron configuration from adding the eight electrons also differ.
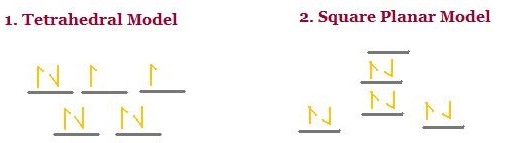
The tetrahedral geometry has two unpaired electrons and the square planer geometry has zero. Since \(ZnI_4\) is diamagnetic, it must have a square planar geometry.
For each of the following coordination complexes, identify if it is paramagnetic or diamagnetic?
- octahedral, low spin, \(d^4\),
- octahedral, low spin, \(d^6\),
- tetrahedral, low spin, \(d^4\)
- square planar, low spin, \(d^8\)
Measuring the Strength of Magnetism
The Gouy balance is used to measure paramagnetism by suspending the complex in question against an equivalent weight with access to a magnetic field. In principle, a magnetic measurement can be done very simply. All it takes is a balance and a magnetic field. We all know how a balance works. In a simple model from an earlier time, we place the sample in one pan. The balance tips over. We find the appropriate weight - a little piece of carefully prepared metal, certified by some bureau of standards. The balance balances. The masses in the two pans must be equal.

With a Gouy balance, the same idea applies, but we throw in a magnetic field, too. Even when it should be balanced, the balance tips, because of an attraction to the magnetic field. We need to find another weight that will get the balance even again. The weight needed to balance the scale is proportional to the attraction of the material to the magnetic field.

If the compound is paramagnetic, it will be pulled visibly towards the electromagnet, which is the distance proportional to the magnitude of the compound's paramagnetism. If the compound, however, is diamagnetic, it will not be pulled towards the electromagnet, instead, it might even slightly be repelled by it. This will be proven by the decreased weight or the no change in weight. The change in weight directly corresponds to the amount of unpaired electrons in the compound.
References
- Petrucci [ chapter 23. p. 968 and chapter 24 section 24-5].
- Johnson, Ronald C. and Basolo, Fred, "Coordination Chemistry: The Chemistry of Metal Complexes, W. A. Benjamin, Inc. pp40-44. 1964
- Jones, Mark M. Elementary Coordination Chemistry Prentice-Hall, Inc. 1964
Contributors and Attributions
- Neele Holzenkaempfer, Jesse Gipe
Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

