18.2: Relationship Between Solubility and Ksp
- Page ID
- 24306
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Quantitatively related \(K_{sp}\) to solubility
Considering the relation between solubility and \(K_{sp}\) is important when describing the solubility of slightly ionic compounds. However, this article discusses ionic compounds that are difficult to dissolve; they are considered "slightly soluble" or "almost insoluble." Solubility product constants (\(K_{sq}\)) are given to those solutes, and these constants can be used to find the molar solubility of the compounds that make the solute. This relationship also facilitates finding the \(K_{sq}\) of a slightly soluble solute from its solubility.
Introduction
Recall that the definition of solubility is the maximum possible concentration of a solute in a solution at a given temperature and pressure. We can determine the solubility product of a slightly soluble solid from that measure of its solubility at a given temperature and pressure, provided that the only significant reaction that occurs when the solid dissolves is its dissociation into solvated ions, that is, the only equilibrium involved is:
\[\ce{M}_p\ce{X}_q(s)⇌p\mathrm{M^{m+}}(aq)+q\mathrm{X^{n−}}(aq)\]
In this case, we calculate the solubility product by taking the solid’s solubility expressed in units of moles per liter (mol/L), known as its molar solubility.
We began the chapter with an informal discussion of how the mineral fluorite is formed. Fluorite, \(\ce{CaF2}\), is a slightly soluble solid that dissolves according to the equation:
\[\ce{CaF2}(s)⇌\ce{Ca^2+}(aq)+\ce{2F-}(aq)\nonumber \]
The concentration of Ca2+ in a saturated solution of CaF2 is 2.1 × 10–4 M; therefore, that of F– is 4.2 × 10–4 M, that is, twice the concentration of \(\ce{Ca^{2+}}\). What is the solubility product of fluorite?
Solution
First, write out the Ksp expression, then substitute in concentrations and solve for Ksp:
\[\ce{CaF2(s) <=> Ca^{2+}(aq) + 2F^{-}(aq)} \nonumber\]
A saturated solution is a solution at equilibrium with the solid. Thus:
\[\begin{align*} K_\ce{sp} &= \ce{[Ca^{2+}][F^{-}]^2} \\[4pt] &=(2.1×10^{−4})(4.2×10^{−4})^2 \\[4pt] &=3.7×10^{−11}\end{align*}\]
As with other equilibrium constants, we do not include units with Ksp.
In a saturated solution that is in contact with solid Mg(OH)2, the concentration of Mg2+ is 3.7 × 10–5 M. What is the solubility product for Mg(OH)2?
\[\ce{Mg(OH)2}(s)⇌\ce{Mg^2+}(aq)+\ce{2OH-}(aq)\nonumber\]
- Answer
-
2.0 × 10–13
The Ksp of copper(I) bromide, \(\ce{CuBr}\), is 6.3 × 10–9. Calculate the molar solubility of copper bromide.
Solution
The solubility product constant of copper(I) bromide is 6.3 × 10–9.
The reaction is:
\[\ce{CuBr}(s)⇌\ce{Cu+}(aq)+\ce{Br-}(aq)\nonumber\]
First, write out the solubility product equilibrium constant expression:
\[K_\ce{sp}=\ce{[Cu+][Br- ]}\nonumber\]
Create an ICE table (as introduced in the chapter on fundamental equilibrium concepts), leaving the \(\ce{CuBr}\) column empty as it is a solid and does not contribute to the Ksp: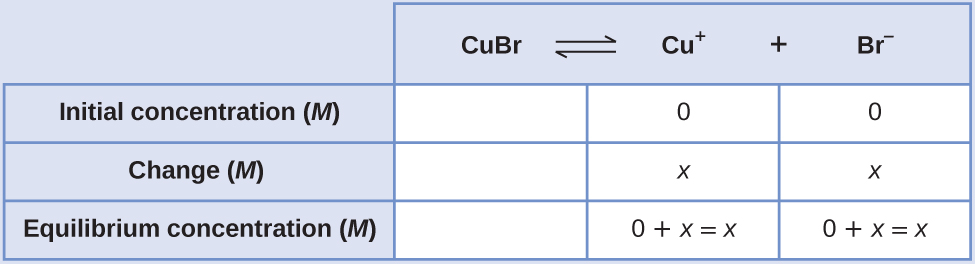
At equilibrium:
\[ \begin{align*} K_\ce{sp} &=\ce{[Cu+][Br- ]} \\[4pt] 6.3×10^{−9} &=(x)(x)=x^2 \\[4pt] x&=\sqrt{(6.3×10^{−9})}=7.9×10^{−5} \end{align*}\]
Therefore, the molar solubility of \(\ce{CuBr}\) is 7.9 × 10–5 M.
Finding the Solubility of a Salt: https://youtu.be/98BuldrICXM
Summary
Solubility is defined as the maximum amount of solute that can be dissolved in a solvent at equilibrium. Equilibrium is the state at which the concentrations of products and reactant are constant after the reaction has taken place. The solubility product constant (\(K_{sp}\)) describes the equilibrium between a solid and its constituent ions in a solution. The value of the constant identifies the degree to which the compound can dissociate in water. The higher the \(K_{sp}\), the more soluble the compound is. \(K_{sq}\) is defined in terms of activity rather than concentration because it is a measure of a concentration that depends on certain conditions such as temperature, pressure, and composition. It is influenced by surroundings. \(K_{sp}\) is used to describe the saturated solution of ionic compounds. (A saturated solution is in a state of equilibrium between the dissolved, dissociated, undissolved solid, and the ionic compound.)
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).